TRADE: Transfer of Distributions between External Conditions with Normalizing Flows

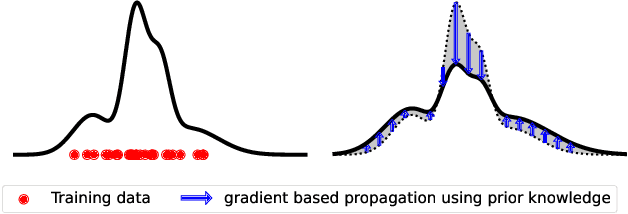
Modeling distributions that depend on external control parameters is a common scenario in diverse applications like molecular simulations, where system properties like temperature affect molecular configurations. Despite the relevance of these applications, existing solutions are unsatisfactory as they require severely restricted model architectures or rely on backward training, which is prone to unstable training. We introduce TRADE, which overcomes these limitations by formulating the learning process as a boundary value problem. By initially training the model for a specific condition using either i.i.d. samples or backward KL training, we establish a boundary distribution. We then propagate this information across other conditions using the gradient of the unnormalized density with respect to the external parameter. This formulation, akin to the principles of physics-informed neural networks, allows us to efficiently learn parameter-dependent distributions without restrictive assumptions. Experimentally, we demonstrate that TRADE achieves excellent results in a wide range of applications, ranging from Bayesian inference and molecular simulations to physical lattice models.

On the Universality of Coupling-based Normalizing Flows

We present a novel theoretical framework for understanding the expressive power of coupling-based normalizing flows such as RealNVP. Despite their prevalence in scientific applications, a comprehensive understanding of coupling flows remains elusive due to their restricted architectures. Existing theorems fall short as they require the use of arbitrarily ill-conditioned neural networks, limiting practical applicability. Additionally, we demonstrate that these constructions inherently lead to volume-preserving flows, a property which we show to be a fundamental constraint for expressivity. We propose a new distributional universality theorem for coupling-based normalizing flows, which overcomes several limitations of prior work. Our results support the general wisdom that the coupling architecture is expressive and provide a nuanced view for choosing the expressivity of coupling functions, bridging a gap between empirical results and theoretical understanding.