Learning Distributions on Manifolds with Free-form Flows
Paper and Code
Dec 15, 2023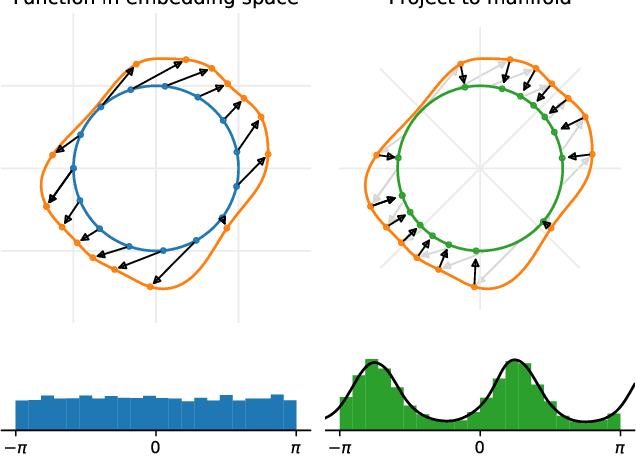

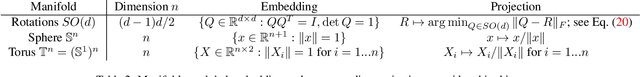
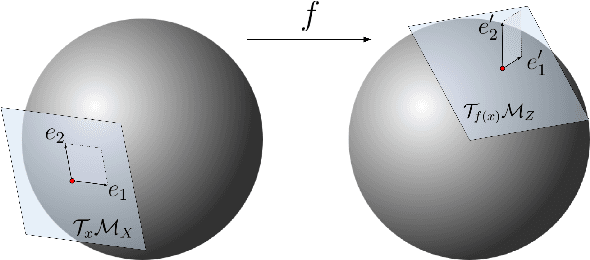
Many real world data, particularly in the natural sciences and computer vision, lie on known Riemannian manifolds such as spheres, tori or the group of rotation matrices. The predominant approaches to learning a distribution on such a manifold require solving a differential equation in order to sample from the model and evaluate densities. The resulting sampling times are slowed down by a high number of function evaluations. In this work, we propose an alternative approach which only requires a single function evaluation followed by a projection to the manifold. Training is achieved by an adaptation of the recently proposed free-form flow framework to Riemannian manifolds. The central idea is to estimate the gradient of the negative log-likelihood via a trace evaluated in the tangent space. We evaluate our method on various manifolds, and find significantly faster inference at competitive performance compared to previous work. We make our code public at https://github.com/vislearn/FFF.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge