Learning Distances from Data with Normalizing Flows and Score Matching

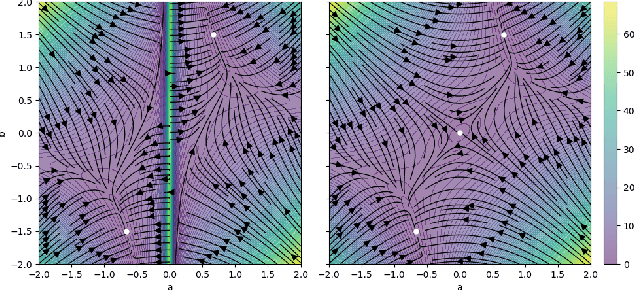
Density-based distances (DBDs) offer an elegant solution to the problem of metric learning. By defining a Riemannian metric which increases with decreasing probability density, shortest paths naturally follow the data manifold and points are clustered according to the modes of the data. We show that existing methods to estimate Fermat distances, a particular choice of DBD, suffer from poor convergence in both low and high dimensions due to i) inaccurate density estimates and ii) reliance on graph-based paths which are increasingly rough in high dimensions. To address these issues, we propose learning the densities using a normalizing flow, a generative model with tractable density estimation, and employing a smooth relaxation method using a score model initialized from a graph-based proposal. Additionally, we introduce a dimension-adapted Fermat distance that exhibits more intuitive behavior when scaled to high dimensions and offers better numerical properties. Our work paves the way for practical use of density-based distances, especially in high-dimensional spaces.

Learning Distributions on Manifolds with Free-form Flows

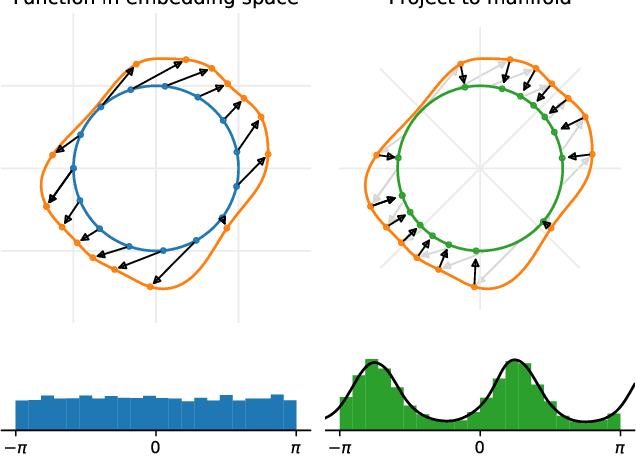
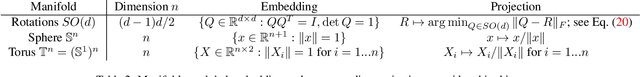
Many real world data, particularly in the natural sciences and computer vision, lie on known Riemannian manifolds such as spheres, tori or the group of rotation matrices. The predominant approaches to learning a distribution on such a manifold require solving a differential equation in order to sample from the model and evaluate densities. The resulting sampling times are slowed down by a high number of function evaluations. In this work, we propose an alternative approach which only requires a single function evaluation followed by a projection to the manifold. Training is achieved by an adaptation of the recently proposed free-form flow framework to Riemannian manifolds. The central idea is to estimate the gradient of the negative log-likelihood via a trace evaluated in the tangent space. We evaluate our method on various manifolds, and find significantly faster inference at competitive performance compared to previous work. We make our code public at https://github.com/vislearn/FFF.

Free-form Flows: Make Any Architecture a Normalizing Flow

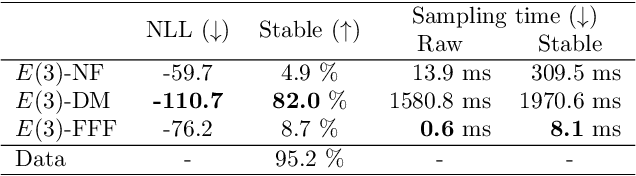
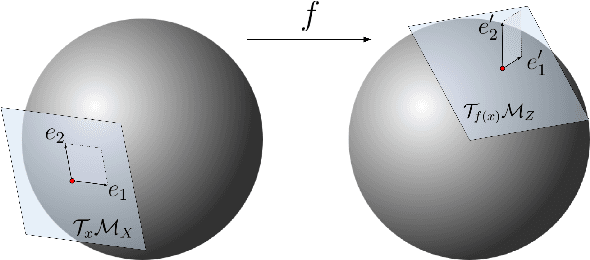
Normalizing Flows are generative models that directly maximize the likelihood. Previously, the design of normalizing flows was largely constrained by the need for analytical invertibility. We overcome this constraint by a training procedure that uses an efficient estimator for the gradient of the change of variables formula. This enables any dimension-preserving neural network to serve as a generative model through maximum likelihood training. Our approach allows placing the emphasis on tailoring inductive biases precisely to the task at hand. Specifically, we achieve excellent results in molecule generation benchmarks utilizing $E(n)$-equivariant networks. Moreover, our method is competitive in an inverse problem benchmark, while employing off-the-shelf ResNet architectures.

Maximum Likelihood Training of Autoencoders

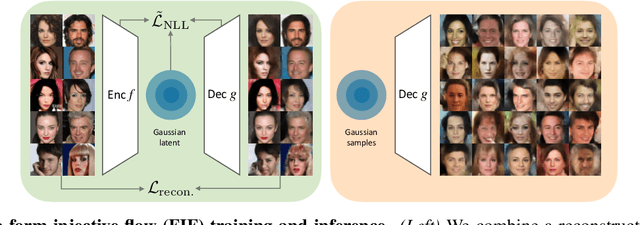
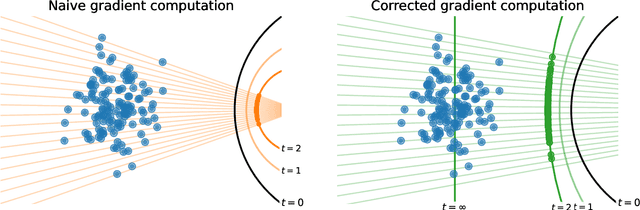
Maximum likelihood training has favorable statistical properties and is popular for generative modeling, especially with normalizing flows. On the other hand, generative autoencoders promise to be more efficient than normalizing flows due to the manifold hypothesis. In this work, we introduce successful maximum likelihood training of unconstrained autoencoders for the first time, bringing the two paradigms together. To do so, we identify and overcome two challenges: Firstly, existing maximum likelihood estimators for free-form networks are unacceptably slow, relying on iteration schemes whose cost scales linearly with latent dimension. We introduce an improved estimator which eliminates iteration, resulting in constant cost (roughly double the runtime per batch of a vanilla autoencoder). Secondly, we demonstrate that naively applying maximum likelihood to autoencoders can lead to divergent solutions and use this insight to motivate a stable maximum likelihood training objective. We perform extensive experiments on toy, tabular and image data, demonstrating the competitive performance of the resulting model. We call our model the maximum likelihood autoencoder (MLAE).

Better Latent Spaces for Better Autoencoders

Autoencoders as tools behind anomaly searches at the LHC have the structural problem that they only work in one direction, extracting jets with higher complexity but not the other way around. To address this, we derive classifiers from the latent space of (variational) autoencoders, specifically in Gaussian mixture and Dirichlet latent spaces. In particular, the Dirichlet setup solves the problem and improves both the performance and the interpretability of the networks.

Disentanglement by Nonlinear ICA with General Incompressible-flow Networks (GIN)

A central question of representation learning asks under which conditions it is possible to reconstruct the true latent variables of an arbitrarily complex generative process. Recent breakthrough work by Khemakhem et al. (2019) on nonlinear ICA has answered this question for a broad class of conditional generative processes. We extend this important result in a direction relevant for application to real-world data. First, we generalize the theory to the case of unknown intrinsic problem dimension and prove that in some special (but not very restrictive) cases, informative latent variables will be automatically separated from noise by an estimating model. Furthermore, the recovered informative latent variables will be in one-to-one correspondence with the true latent variables of the generating process, up to a trivial component-wise transformation. Second, we introduce a modification of the RealNVP invertible neural network architecture (Dinh et al. (2016)) which is particularly suitable for this type of problem: the General Incompressible-flow Network (GIN). Experiments on artificial data and EMNIST demonstrate that theoretical predictions are indeed verified in practice. In particular, we provide a detailed set of exactly 22 informative latent variables extracted from EMNIST.