Lea Zimmermann
Free-form Flows: Make Any Architecture a Normalizing Flow
Oct 25, 2023

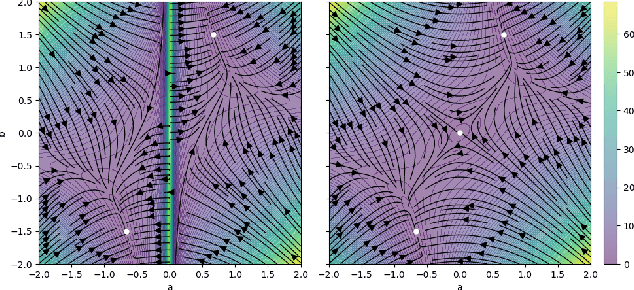
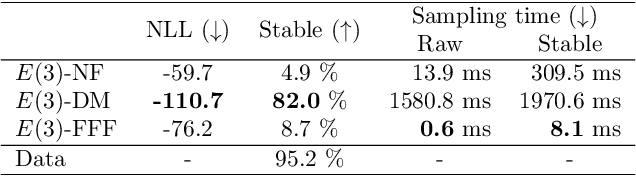
Abstract:Normalizing Flows are generative models that directly maximize the likelihood. Previously, the design of normalizing flows was largely constrained by the need for analytical invertibility. We overcome this constraint by a training procedure that uses an efficient estimator for the gradient of the change of variables formula. This enables any dimension-preserving neural network to serve as a generative model through maximum likelihood training. Our approach allows placing the emphasis on tailoring inductive biases precisely to the task at hand. Specifically, we achieve excellent results in molecule generation benchmarks utilizing $E(n)$-equivariant networks. Moreover, our method is competitive in an inverse problem benchmark, while employing off-the-shelf ResNet architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge