Transforming the Bootstrap: Using Transformers to Compute Scattering Amplitudes in Planar N = 4 Super Yang-Mills Theory

We pursue the use of deep learning methods to improve state-of-the-art computations in theoretical high-energy physics. Planar N = 4 Super Yang-Mills theory is a close cousin to the theory that describes Higgs boson production at the Large Hadron Collider; its scattering amplitudes are large mathematical expressions containing integer coefficients. In this paper, we apply Transformers to predict these coefficients. The problem can be formulated in a language-like representation amenable to standard cross-entropy training objectives. We design two related experiments and show that the model achieves high accuracy (> 98%) on both tasks. Our work shows that Transformers can be applied successfully to problems in theoretical physics that require exact solutions.

Structures of Neural Network Effective Theories

We develop a diagrammatic approach to effective field theories (EFTs) corresponding to deep neural networks at initialization, which dramatically simplifies computations of finite-width corrections to neuron statistics. The structures of EFT calculations make it transparent that a single condition governs criticality of all connected correlators of neuron preactivations. Understanding of such EFTs may facilitate progress in both deep learning and field theory simulations.

Linearized Optimal Transport for Collider Events

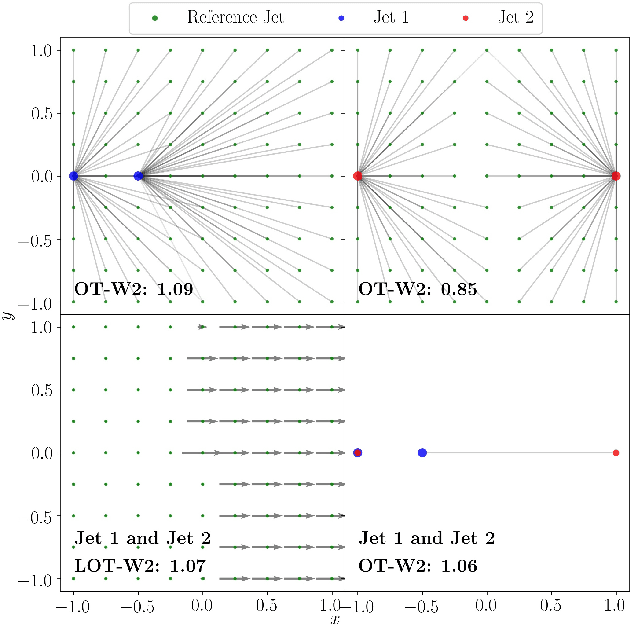
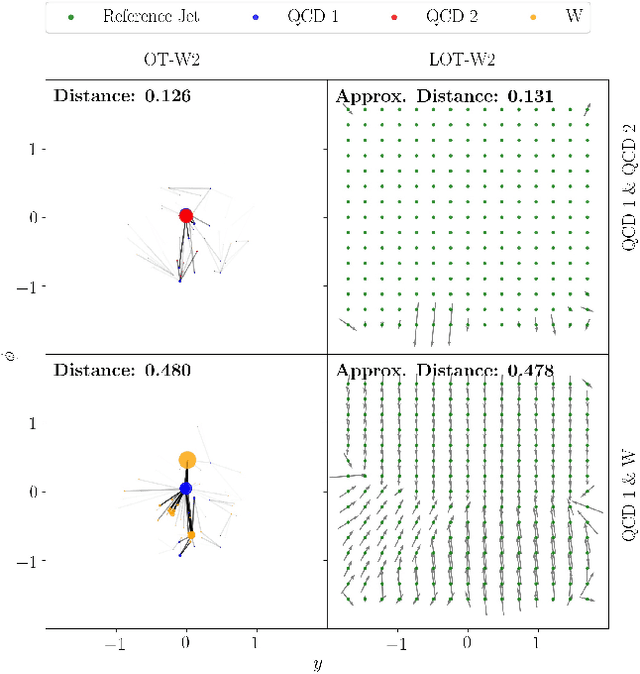
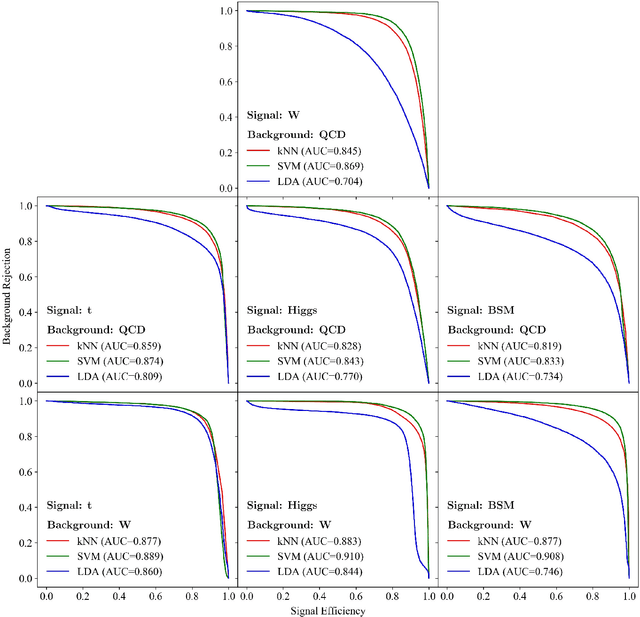
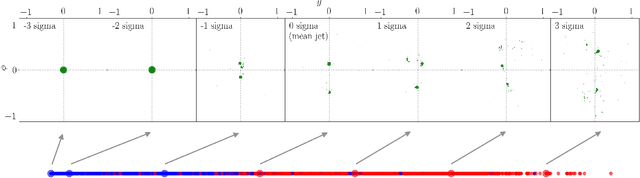
We introduce an efficient framework for computing the distance between collider events using the tools of Linearized Optimal Transport (LOT). This preserves many of the advantages of the recently-introduced Energy Mover's Distance, which quantifies the "work" required to rearrange one event into another, while significantly reducing the computational cost. It also furnishes a Euclidean embedding amenable to simple machine learning algorithms and visualization techniques, which we demonstrate in a variety of jet tagging examples. The LOT approximation lowers the threshold for diverse applications of the theory of optimal transport to collider physics.