Structures of Neural Network Effective Theories

We develop a diagrammatic approach to effective field theories (EFTs) corresponding to deep neural networks at initialization, which dramatically simplifies computations of finite-width corrections to neuron statistics. The structures of EFT calculations make it transparent that a single condition governs criticality of all connected correlators of neuron preactivations. Understanding of such EFTs may facilitate progress in both deep learning and field theory simulations.

Linearized Optimal Transport for Collider Events

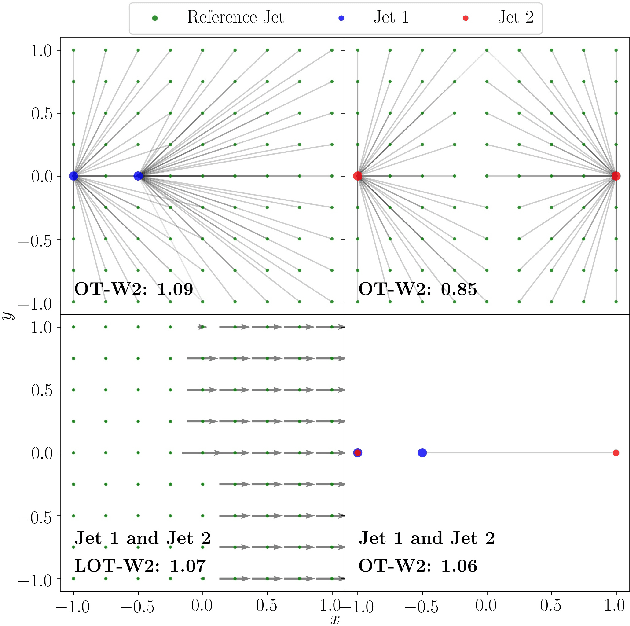
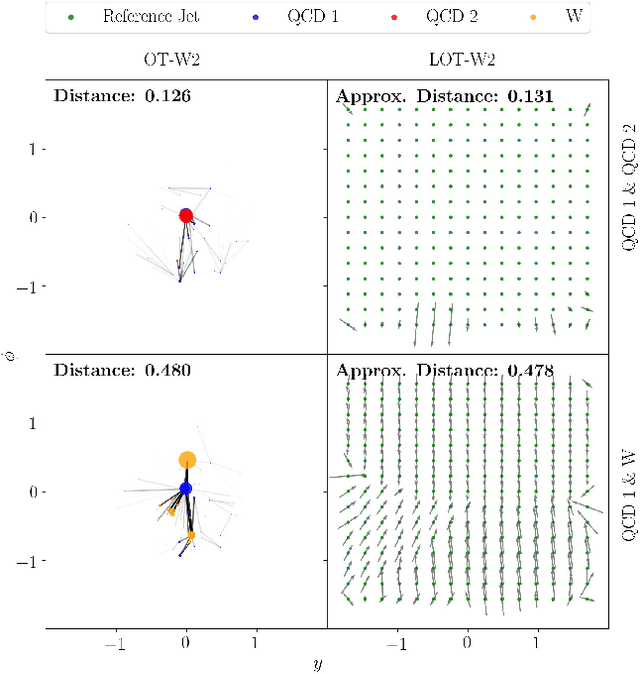
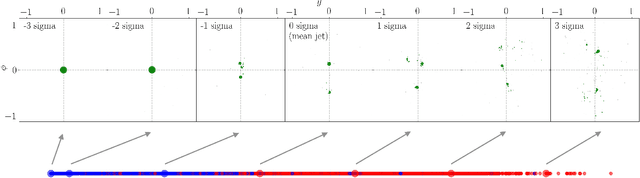
We introduce an efficient framework for computing the distance between collider events using the tools of Linearized Optimal Transport (LOT). This preserves many of the advantages of the recently-introduced Energy Mover's Distance, which quantifies the "work" required to rearrange one event into another, while significantly reducing the computational cost. It also furnishes a Euclidean embedding amenable to simple machine learning algorithms and visualization techniques, which we demonstrate in a variety of jet tagging examples. The LOT approximation lowers the threshold for diverse applications of the theory of optimal transport to collider physics.