Linearized Optimal Transport for Collider Events
Paper and Code
Aug 19, 2020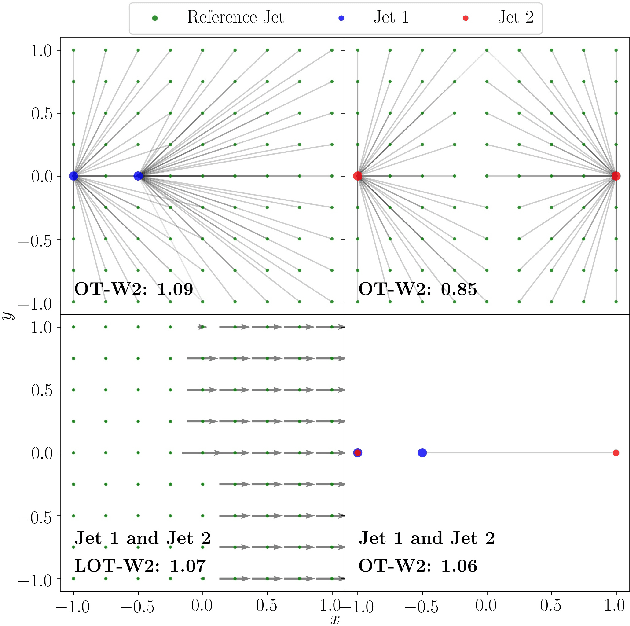
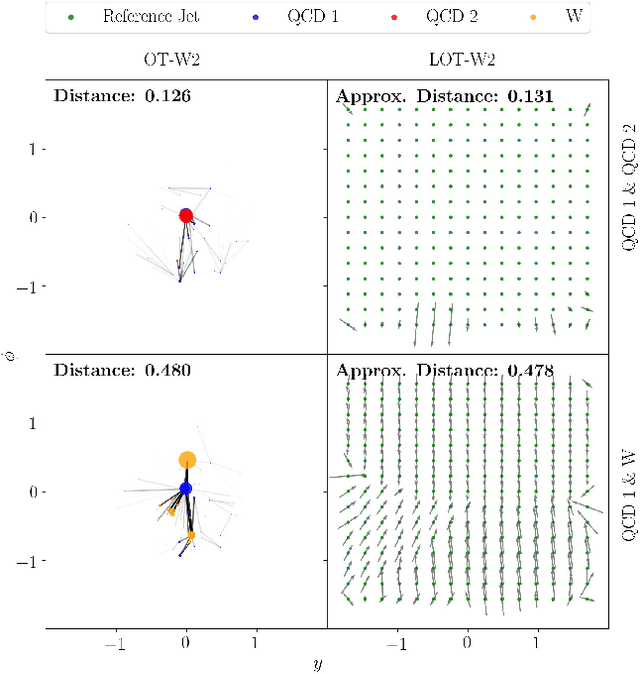
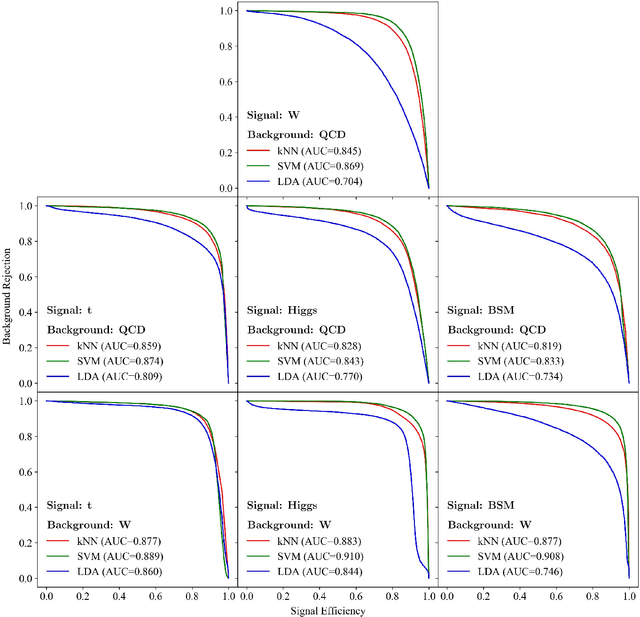
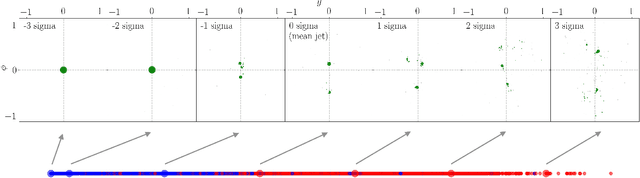
We introduce an efficient framework for computing the distance between collider events using the tools of Linearized Optimal Transport (LOT). This preserves many of the advantages of the recently-introduced Energy Mover's Distance, which quantifies the "work" required to rearrange one event into another, while significantly reducing the computational cost. It also furnishes a Euclidean embedding amenable to simple machine learning algorithms and visualization techniques, which we demonstrate in a variety of jet tagging examples. The LOT approximation lowers the threshold for diverse applications of the theory of optimal transport to collider physics.
* 16 pages, 5 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge