Roshan Dathathri
The University of Texas at Austin
MSCCL++: Rethinking GPU Communication Abstractions for Cutting-edge AI Applications
Apr 11, 2025

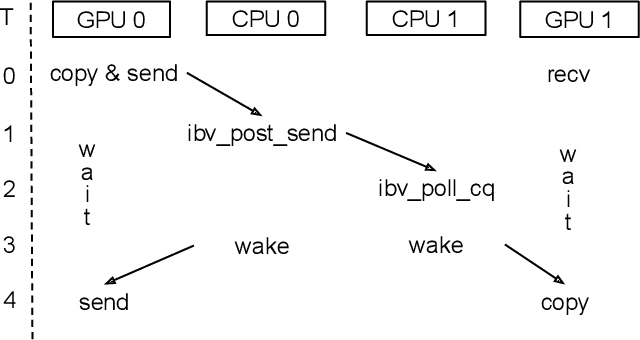
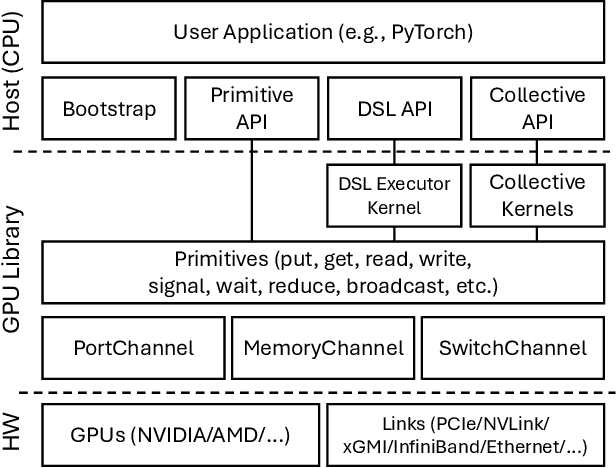
Abstract:Modern cutting-edge AI applications are being developed over fast-evolving, heterogeneous, nascent hardware devices. This requires frequent reworking of the AI software stack to adopt bottom-up changes from new hardware, which takes time for general-purpose software libraries. Consequently, real applications often develop custom software stacks optimized for their specific workloads and hardware. Custom stacks help quick development and optimization, but incur a lot of redundant efforts across applications in writing non-portable code. This paper discusses an alternative communication library interface for AI applications that offers both portability and performance by reducing redundant efforts while maintaining flexibility for customization. We present MSCCL++, a novel abstraction of GPU communication based on separation of concerns: (1) a primitive interface provides a minimal hardware abstraction as a common ground for software and hardware developers to write custom communication, and (2) higher-level portable interfaces and specialized implementations enable optimization for different hardware environments. This approach makes the primitive interface reusable across applications while enabling highly flexible optimization. Compared to state-of-the-art baselines (NCCL, RCCL, and MSCCL), MSCCL++ achieves speedups of up to 3.8$\times$ for collective communication and up to 15\% for real-world AI inference workloads. MSCCL++ is in production of multiple AI services provided by Microsoft Azure, and is also adopted by RCCL, the GPU collective communication library maintained by AMD. MSCCL++ is open-source and available at https://github.com/microsoft/mscclpp.
Optimizing Graph Transformer Networks with Graph-based Techniques
Jun 16, 2021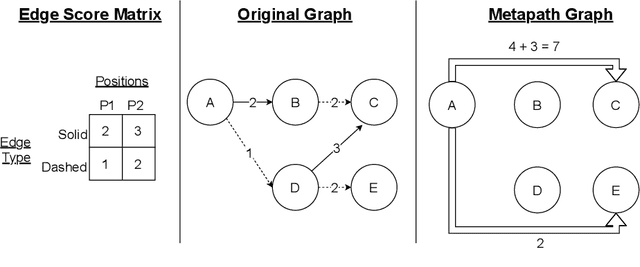
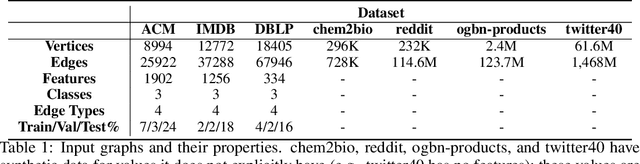
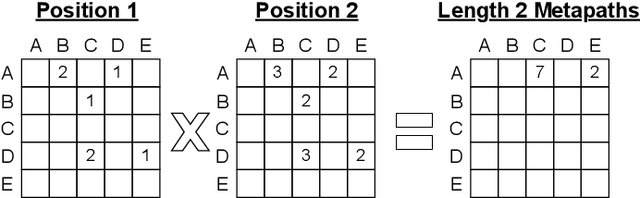
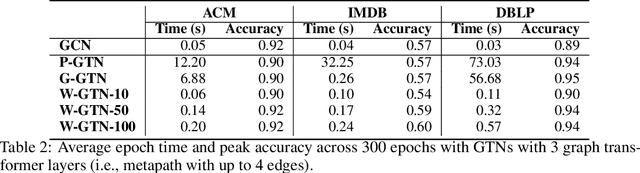
Abstract:Graph transformer networks (GTN) are a variant of graph convolutional networks (GCN) that are targeted to heterogeneous graphs in which nodes and edges have associated type information that can be exploited to improve inference accuracy. GTNs learn important metapaths in the graph, create weighted edges for these metapaths, and use the resulting graph in a GCN. Currently, the only available implementation of GTNs uses dense matrix multiplication to find metapaths. Unfortunately, the space overhead of this approach can be large, so in practice it is used only for small graphs. In addition, the matrix-based implementation is not fine-grained enough to use random-walk based methods to optimize metapath finding. In this paper, we present a graph-based formulation and implementation of the GTN metapath finding problem. This graph-based formulation has two advantages over the matrix-based approach. First, it is more space efficient than the original GTN implementation and more compute-efficient for metapath sizes of practical interest. Second, it permits us to implement a sampling method that reduces the number of metapaths that must be enumerated, allowing the implementation to be used for larger graphs and larger metapath sizes. Experimental results show that our implementation is $6.5\times$ faster than the original GTN implementation on average for a metapath length of 4, and our sampling implementation is $155\times$ faster on average than this implementation without compromising on the accuracy of the GTN.
EVA: An Encrypted Vector Arithmetic Language and Compiler for Efficient Homomorphic Computation
Dec 27, 2019
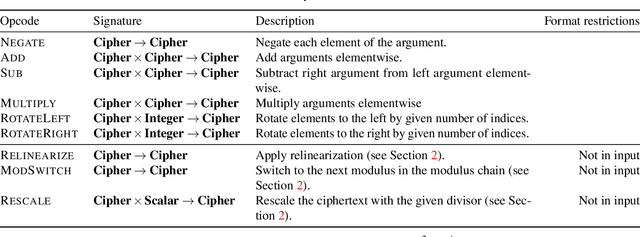
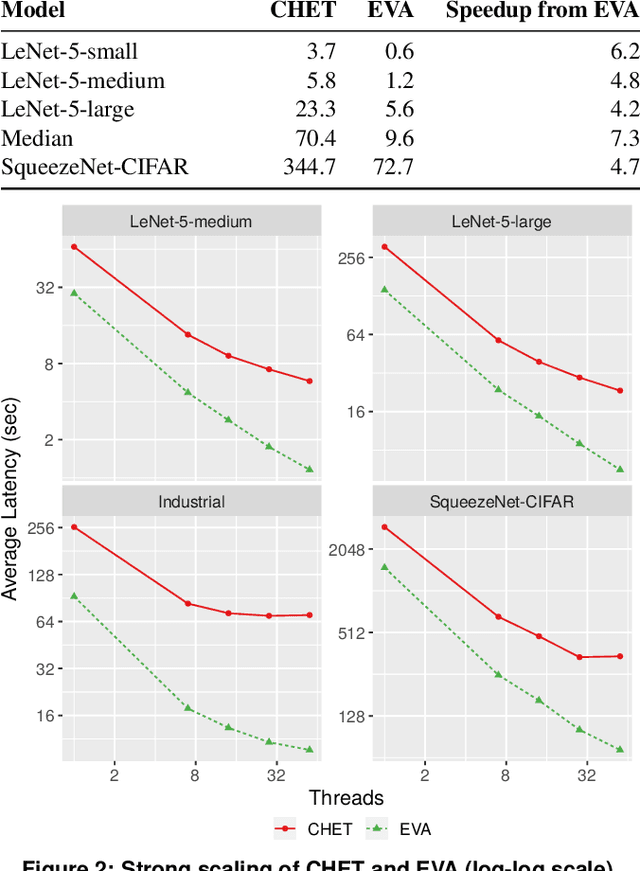
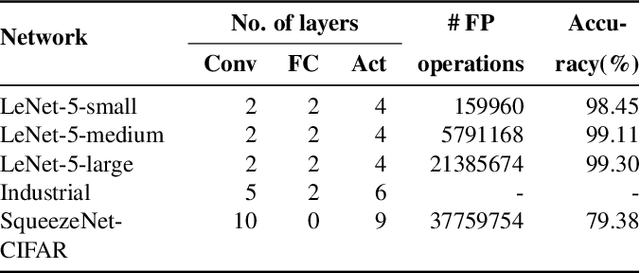
Abstract:Fully-Homomorphic Encryption (FHE) offers powerful capabilities by enabling secure offloading of both storage and computation, and recent innovations in schemes and implementation have made it all the more attractive. At the same time, FHE is notoriously hard to use with a very constrained programming model, a very unusual performance profile, and many cryptographic constraints. Existing compilers for FHE either target simpler but less efficient FHE schemes or only support specific domains where they can rely on expert provided high-level runtimes to hide complications. This paper presents a new FHE language called Encrypted Vector Arithmetic (EVA), which includes an optimizing compiler that generates correct and secure FHE programs, while hiding all the complexities of the target FHE scheme. Bolstered by our optimizing compiler, programmers can develop efficient general purpose FHE applications directly in EVA. For example, we have developed image processing applications using EVA, with very few lines of code. EVA is designed to also work as an intermediate representation that can be a target for compiling higher-level domain-specific languages. To demonstrate this we have re-targeted CHET, an existing domain-specific compiler for neural network inference, onto EVA. Due to the novel optimizations in EVA, its programs are on average 5.3x faster than those generated by CHET. We believe EVA would enable a wider adoption of FHE by making it easier to develop FHE applications and domain-specific FHE compilers.
Distributed Word2Vec using Graph Analytics Frameworks
Sep 08, 2019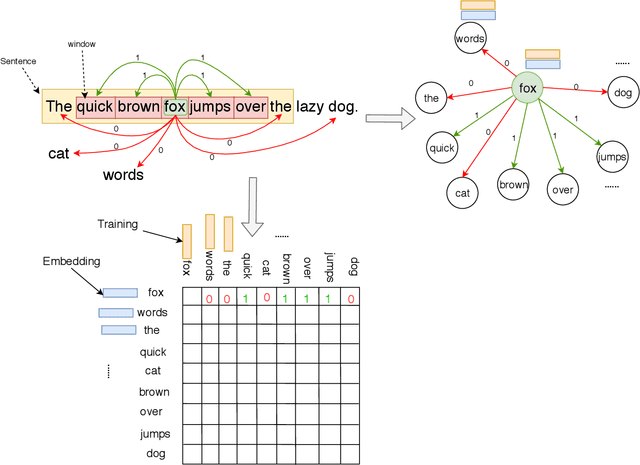
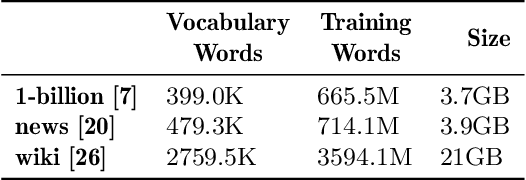
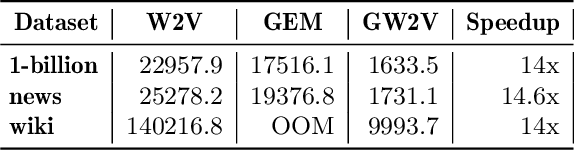
Abstract:Word embeddings capture semantic and syntactic similarities of words, represented as vectors. Word2Vec is a popular implementation of word embeddings; it takes as input a large corpus of text and learns a model that maps unique words in that corpus to other contextually relevant words. After training, Word2Vec's internal vector representation of words in the corpus map unique words to a vector space, which are then used in many downstream tasks. Training these models requires significant computational resources (training time often measured in days) and is difficult to parallelize. Most word embedding training uses stochastic gradient descent (SGD), an "inherently" sequential algorithm where at each step, the processing of the current example depends on the parameters learned from the previous examples. Prior approaches to parallelizing SGD do not honor these dependencies and thus potentially suffer poor convergence. This paper introduces GraphWord2Vec, a distributedWord2Vec algorithm which formulates the Word2Vec training process as a distributed graph problem and thus leverage state-of-the-art distributed graph analytics frameworks such as D-Galois and Gemini that scale to large distributed clusters. GraphWord2Vec also demonstrates how to use model combiners to honor data dependencies in SGD and thus scale without giving up convergence. We will show that GraphWord2Vec has linear scalability up to 32 machines converging as fast as a sequential run in terms of epochs, thus reducing training time by 14x.
CHET: Compiler and Runtime for Homomorphic Evaluation of Tensor Programs
Oct 01, 2018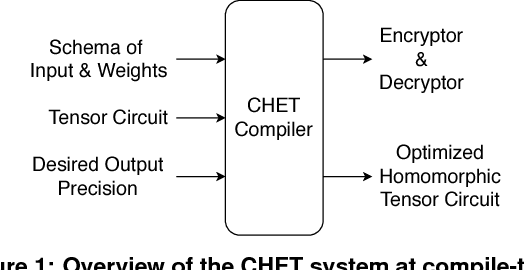
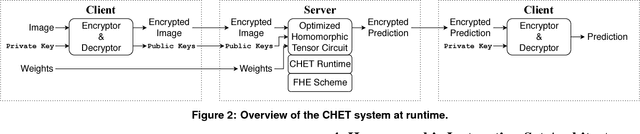
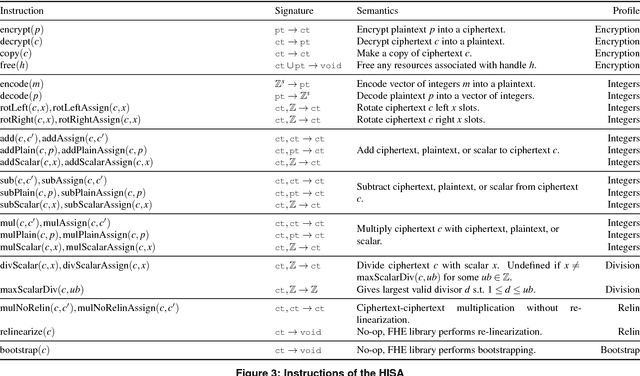
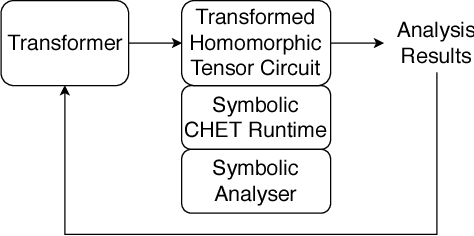
Abstract:Fully Homomorphic Encryption (FHE) refers to a set of encryption schemes that allow computations to be applied directly on encrypted data without requiring a secret key. This enables novel application scenarios where a client can safely offload storage and computation to a third-party cloud provider without having to trust the software and the hardware vendors with the decryption keys. Recent advances in both FHE schemes and implementations have moved such applications from theoretical possibilities into the realm of practicalities. This paper proposes a compact and well-reasoned interface called the Homomorphic Instruction Set Architecture (HISA) for developing FHE applications. Just as the hardware ISA interface enabled hardware advances to proceed independent of software advances in the compiler and language runtimes, HISA decouples compiler optimizations and runtimes for supporting FHE applications from advancements in the underlying FHE schemes. This paper demonstrates the capabilities of HISA by building an end-to-end software stack for evaluating neural network models on encrypted data. Our stack includes an end-to-end compiler, runtime, and a set of optimizations. Our approach shows generated code, on a set of popular neural network architectures, is faster than hand-optimized implementations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge