Investigating Student Interaction Patterns with Large Language Model-Powered Course Assistants in Computer Science Courses

Providing students with flexible and timely academic support is a challenge at most colleges and universities, leaving many students without help outside scheduled hours. Large language models (LLMs) are promising for bridging this gap, but interactions between students and LLMs are rarely overseen by educators. We developed and studied an LLM-powered course assistant deployed across multiple computer science courses to characterize real-world use and understand pedagogical implications. By Spring 2024, our system had been deployed to approximately 2,000 students across six courses at three institutions. Analysis of the interaction data shows that usage remains strong in the evenings and nights and is higher in introductory courses, indicating that our system helps address temporal support gaps and novice learner needs. We sampled 200 conversations per course for manual annotation: most sampled responses were judged correct and helpful, with a small share unhelpful or erroneous; few responses included dedicated examples. We also examined an inquiry-based learning strategy: only around 11% of sampled conversations contained LLM-generated follow-up questions, which were often ignored by students in advanced courses. A Bloom's taxonomy analysis reveals that current LLM capabilities are limited in generating higher-order cognitive questions. These patterns suggest opportunities for pedagogically oriented LLM-based educational systems and greater educator involvement in configuring prompts, content, and policies.

BatchGNN: Efficient CPU-Based Distributed GNN Training on Very Large Graphs

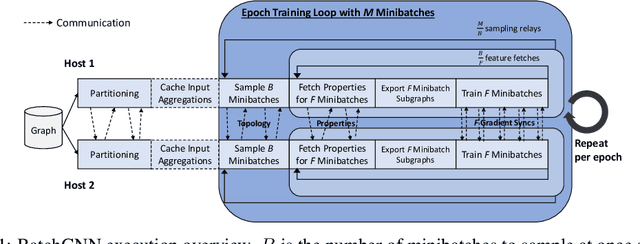
We present BatchGNN, a distributed CPU system that showcases techniques that can be used to efficiently train GNNs on terabyte-sized graphs. It reduces communication overhead with macrobatching in which multiple minibatches' subgraph sampling and feature fetching are batched into one communication relay to reduce redundant feature fetches when input features are static. BatchGNN provides integrated graph partitioning and native GNN layer implementations to improve runtime, and it can cache aggregated input features to further reduce sampling overhead. BatchGNN achieves an average $3\times$ speedup over DistDGL on three GNN models trained on OGBN graphs, outperforms the runtimes reported by distributed GPU systems $P^3$ and DistDGLv2, and scales to a terabyte-sized graph.

Optimizing Graph Transformer Networks with Graph-based Techniques

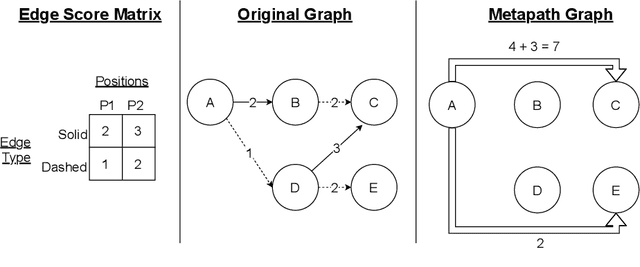
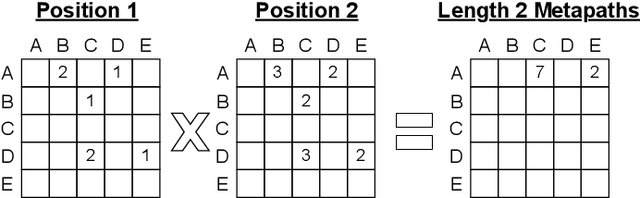
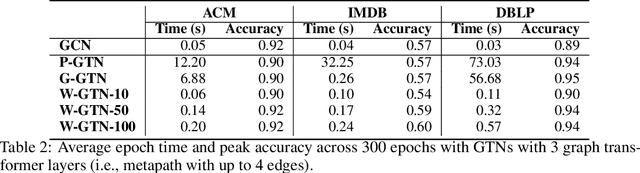
Graph transformer networks (GTN) are a variant of graph convolutional networks (GCN) that are targeted to heterogeneous graphs in which nodes and edges have associated type information that can be exploited to improve inference accuracy. GTNs learn important metapaths in the graph, create weighted edges for these metapaths, and use the resulting graph in a GCN. Currently, the only available implementation of GTNs uses dense matrix multiplication to find metapaths. Unfortunately, the space overhead of this approach can be large, so in practice it is used only for small graphs. In addition, the matrix-based implementation is not fine-grained enough to use random-walk based methods to optimize metapath finding. In this paper, we present a graph-based formulation and implementation of the GTN metapath finding problem. This graph-based formulation has two advantages over the matrix-based approach. First, it is more space efficient than the original GTN implementation and more compute-efficient for metapath sizes of practical interest. Second, it permits us to implement a sampling method that reduces the number of metapaths that must be enumerated, allowing the implementation to be used for larger graphs and larger metapath sizes. Experimental results show that our implementation is $6.5\times$ faster than the original GTN implementation on average for a metapath length of 4, and our sampling implementation is $155\times$ faster on average than this implementation without compromising on the accuracy of the GTN.