MLLM-FL: Multimodal Large Language Model Assisted Federated Learning on Heterogeneous and Long-tailed Data

Previous studies on federated learning (FL) often encounter performance degradation due to data heterogeneity among different clients. In light of the recent advances in multimodal large language models (MLLMs), such as GPT-4v and LLaVA, which demonstrate their exceptional proficiency in multimodal tasks, such as image captioning and multimodal question answering. We introduce a novel federated learning framework, named Multimodal Large Language Model Assisted Federated Learning (MLLM-FL), which which employs powerful MLLMs at the server end to address the heterogeneous and long-tailed challenges. Owing to the advanced cross-modality representation capabilities and the extensive open-vocabulary prior knowledge of MLLMs, our framework is adept at harnessing the extensive, yet previously underexploited, open-source data accessible from websites and powerful server-side computational resources. Hence, the MLLM-FL not only enhances the performance but also avoids increasing the risk of privacy leakage and the computational burden on local devices, distinguishing it from prior methodologies. Our framework has three key stages. Initially, prior to local training on local datasets of clients, we conduct global visual-text pretraining of the model. This pretraining is facilitated by utilizing the extensive open-source data available online, with the assistance of multimodal large language models. Subsequently, the pretrained model is distributed among various clients for local training. Finally, once the locally trained models are transmitted back to the server, a global alignment is carried out under the supervision of MLLMs to further enhance the performance. Experimental evaluations on established benchmarks, show that our framework delivers promising performance in the typical scenarios with data heterogeneity and long-tail distribution across different clients in FL.

FVEL: Interactive Formal Verification Environment with Large Language Models via Theorem Proving

Formal verification (FV) has witnessed growing significance with current emerging program synthesis by the evolving large language models (LLMs). However, current formal verification mainly resorts to symbolic verifiers or hand-craft rules, resulting in limitations for extensive and flexible verification. On the other hand, formal languages for automated theorem proving, such as Isabelle, as another line of rigorous verification, are maintained with comprehensive rules and theorems. In this paper, we propose FVEL, an interactive Formal Verification Environment with LLMs. Specifically, FVEL transforms a given code to be verified into Isabelle, and then conducts verification via neural automated theorem proving with an LLM. The joined paradigm leverages the rigorous yet abundant formulated and organized rules in Isabelle and is also convenient for introducing and adjusting cutting-edge LLMs. To achieve this goal, we extract a large-scale FVELER3. The FVELER dataset includes code dependencies and verification processes that are formulated in Isabelle, containing 758 theories, 29,125 lemmas, and 200,646 proof steps in total with in-depth dependencies. We benchmark FVELER in the FVEL environment by first fine-tuning LLMs with FVELER and then evaluating them on Code2Inv and SV-COMP. The results show that FVEL with FVELER fine-tuned Llama3- 8B solves 17.39% (69 -> 81) more problems, and Mistral-7B 12% (75 -> 84) more problems in SV-COMP. And the proportion of proof errors is reduced. Project page: https://fveler.github.io/.

Process-Driven Autoformalization in Lean 4

Autoformalization, the conversion of natural language mathematics into formal languages, offers significant potential for advancing mathematical reasoning. However, existing efforts are limited to formal languages with substantial online corpora and struggle to keep pace with rapidly evolving languages like Lean 4. To bridge this gap, we propose a new benchmark \textbf{Form}alization for \textbf{L}ean~\textbf{4} (\textbf{\name}) designed to evaluate the autoformalization capabilities of large language models (LLMs). This benchmark encompasses a comprehensive assessment of questions, answers, formal statements, and proofs. Additionally, we introduce a \textbf{P}rocess-\textbf{S}upervised \textbf{V}erifier (\textbf{PSV}) model that leverages the precise feedback from Lean 4 compilers to enhance autoformalization. Our experiments demonstrate that the PSV method improves autoformalization, enabling higher accuracy using less filtered training data. Furthermore, when fine-tuned with data containing detailed process information, PSV can leverage the data more effectively, leading to more significant improvements in autoformalization for Lean 4. Our dataset and code are available at \url{https://github.com/rookie-joe/PDA}.

Proving Theorems Recursively

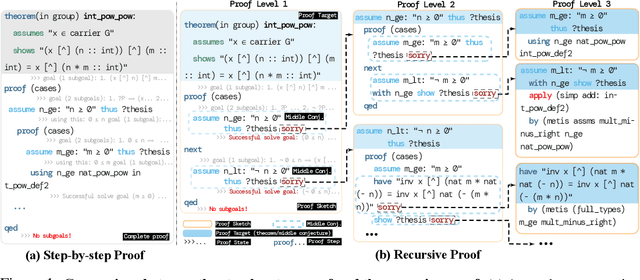
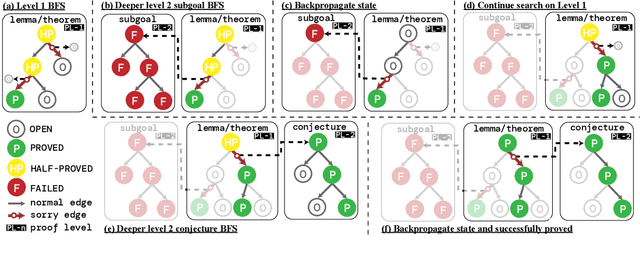
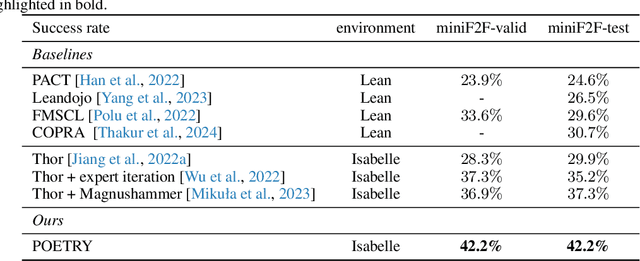
Recent advances in automated theorem proving leverages language models to explore expanded search spaces by step-by-step proof generation. However, such approaches are usually based on short-sighted heuristics (e.g., log probability or value function scores) that potentially lead to suboptimal or even distracting subgoals, preventing us from finding longer proofs. To address this challenge, we propose POETRY (PrOvE Theorems RecursivelY), which proves theorems in a recursive, level-by-level manner in the Isabelle theorem prover. Unlike previous step-by-step methods, POETRY searches for a verifiable sketch of the proof at each level and focuses on solving the current level's theorem or conjecture. Detailed proofs of intermediate conjectures within the sketch are temporarily replaced by a placeholder tactic called sorry, deferring their proofs to subsequent levels. This approach allows the theorem to be tackled incrementally by outlining the overall theorem at the first level and then solving the intermediate conjectures at deeper levels. Experiments are conducted on the miniF2F and PISA datasets and significant performance gains are observed in our POETRY approach over state-of-the-art methods. POETRY on miniF2F achieves an average proving success rate improvement of 5.1%. Moreover, we observe a substantial increase in the maximum proof length found by POETRY, from 10 to 26.

MUSTARD: Mastering Uniform Synthesis of Theorem and Proof Data

Recent large language models (LLMs) have witnessed significant advancement in various tasks, including mathematical reasoning and theorem proving. As these two tasks require strict and formal multi-step inference, they are appealing domains for exploring the reasoning ability of LLMs but still face important challenges. Previous studies such as Chain-of-Thought (CoT) have revealed the effectiveness of intermediate steps guidance. However, such step-wise annotation requires heavy labor, leading to insufficient training steps for current benchmarks. To fill this gap, this work introduces MUSTARD, a data generation framework that masters uniform synthesis of theorem and proof data of high quality and diversity. MUSTARD synthesizes data in three stages: (1) It samples a few mathematical concept seeds as the problem category. (2) Then, it prompts a generative language model with the sampled concepts to obtain both the problems and their step-wise formal solutions. (3) Lastly, the framework utilizes a proof assistant (e.g., Lean Prover) to filter the valid proofs. With the proposed MUSTARD, we present a theorem-and-proof benchmark MUSTARDSAUCE with 5,866 valid data points. Each data point contains an informal statement, an informal proof, and a translated formal proof that passes the prover validation. We perform extensive analysis and demonstrate that MUSTARD generates validated high-quality step-by-step data. We further apply the MUSTARDSAUCE for fine-tuning smaller language models. The fine-tuned Llama 2-7B achieves a 15.41% average relative performance gain in automated theorem proving, and 8.18% in math word problems. Codes and data are available at https://github.com/Eleanor-H/MUSTARD.

TRIGO: Benchmarking Formal Mathematical Proof Reduction for Generative Language Models

Automated theorem proving (ATP) has become an appealing domain for exploring the reasoning ability of the recent successful generative language models. However, current ATP benchmarks mainly focus on symbolic inference, but rarely involve the understanding of complex number combination reasoning. In this work, we propose TRIGO, an ATP benchmark that not only requires a model to reduce a trigonometric expression with step-by-step proofs but also evaluates a generative LM's reasoning ability on formulas and its capability to manipulate, group, and factor number terms. We gather trigonometric expressions and their reduced forms from the web, annotate the simplification process manually, and translate it into the Lean formal language system. We then automatically generate additional examples from the annotated samples to expand the dataset. Furthermore, we develop an automatic generator based on Lean-Gym to create dataset splits of varying difficulties and distributions in order to thoroughly analyze the model's generalization ability. Our extensive experiments show our proposed TRIGO poses a new challenge for advanced generative LM's including GPT-4 which is pre-trained on a considerable amount of open-source formal theorem-proving language data, and provide a new tool to study the generative LM's ability on both formal and mathematical reasoning.

DQ-LoRe: Dual Queries with Low Rank Approximation Re-ranking for In-Context Learning

Recent advances in natural language processing, primarily propelled by Large Language Models (LLMs), have showcased their remarkable capabilities grounded in in-context learning. A promising avenue for guiding LLMs in intricate reasoning tasks involves the utilization of intermediate reasoning steps within the Chain-of-Thought (CoT) paradigm. Nevertheless, the central challenge lies in the effective selection of exemplars for facilitating in-context learning. In this study, we introduce a framework that leverages Dual Queries and Low-rank approximation Re-ranking (DQ-LoRe) to automatically select exemplars for in-context learning. Dual Queries first query LLM to obtain LLM-generated knowledge such as CoT, then query the retriever to obtain the final exemplars via both question and the knowledge. Moreover, for the second query, LoRe employs dimensionality reduction techniques to refine exemplar selection, ensuring close alignment with the input question's knowledge. Through extensive experiments, we demonstrate that DQ-LoRe significantly outperforms prior state-of-the-art methods in the automatic selection of exemplars for GPT-4, enhancing performance from 92.5% to 94.2%. Our comprehensive analysis further reveals that DQ-LoRe consistently outperforms retrieval-based approaches in terms of both performance and adaptability, especially in scenarios characterized by distribution shifts. DQ-LoRe pushes the boundaries of in-context learning and opens up new avenues for addressing complex reasoning challenges. We will release the code soon.

LEGO-Prover: Neural Theorem Proving with Growing Libraries

Despite the success of large language models (LLMs), the task of theorem proving still remains one of the hardest reasoning tasks that is far from being fully solved. Prior methods using language models have demonstrated promising results, but they still struggle to prove even middle school level theorems. One common limitation of these methods is that they assume a fixed theorem library during the whole theorem proving process. However, as we all know, creating new useful theorems or even new theories is not only helpful but crucial and necessary for advancing mathematics and proving harder and deeper results. In this work, we present LEGO-Prover, which employs a growing skill library containing verified lemmas as skills to augment the capability of LLMs used in theorem proving. By constructing the proof modularly, LEGO-Prover enables LLMs to utilize existing skills retrieved from the library and to create new skills during the proving process. These skills are further evolved (by prompting an LLM) to enrich the library on another scale. Modular and reusable skills are constantly added to the library to enable tackling increasingly intricate mathematical problems. Moreover, the learned library further bridges the gap between human proofs and formal proofs by making it easier to impute missing steps. LEGO-Prover advances the state-of-the-art pass rate on miniF2F-valid (48.0% to 57.0%) and miniF2F-test (45.5% to 47.1%). During the proving process, LEGO-Prover also manages to generate over 20,000 skills (theorems/lemmas) and adds them to the growing library. Our ablation study indicates that these newly added skills are indeed helpful for proving theorems, resulting in an improvement from a success rate of 47.1% to 50.4%. We also release our code and all the generated skills.

Lyra: Orchestrating Dual Correction in Automated Theorem Proving

Large Language Models (LLMs) present an intriguing avenue for exploration in the field of formal theorem proving. Nevertheless, their full potential, particularly concerning the mitigation of hallucinations and refinement through prover error messages, remains an area that has yet to be thoroughly investigated. To enhance the effectiveness of LLMs in the field, we introduce the Lyra, a new framework that employs two distinct correction mechanisms: Tool Correction (TC) and Conjecture Correction (CC). To implement Tool Correction in the post-processing of formal proofs, we leverage prior knowledge to utilize predefined prover tools (e.g., Sledgehammer) for guiding the replacement of incorrect tools. Tool Correction significantly contributes to mitigating hallucinations, thereby improving the overall accuracy of the proof. In addition, we introduce Conjecture Correction, an error feedback mechanism designed to interact with prover to refine formal proof conjectures with prover error messages. Compared to the previous refinement framework, the proposed Conjecture Correction refines generation with instruction but does not collect paired (generation, error & refinement) prompts. Our method has achieved state-of-the-art (SOTA) performance on both miniF2F validation (48.0% -> 55.3%) and test (45.5% -> 51.2%). We also present 3 IMO problems solved by Lyra. We believe Tool Correction (post-process for hallucination mitigation) and Conjecture Correction (subgoal adjustment from interaction with environment) could provide a promising avenue for future research in this field.

FIMO: A Challenge Formal Dataset for Automated Theorem Proving

We present FIMO, an innovative dataset comprising formal mathematical problem statements sourced from the International Mathematical Olympiad (IMO) Shortlisted Problems. Designed to facilitate advanced automated theorem proving at the IMO level, FIMO is currently tailored for the Lean formal language. It comprises 149 formal problem statements, accompanied by both informal problem descriptions and their corresponding LaTeX-based informal proofs. Through initial experiments involving GPT-4, our findings underscore the existing limitations in current methodologies, indicating a substantial journey ahead before achieving satisfactory IMO-level automated theorem proving outcomes.