FVEL: Interactive Formal Verification Environment with Large Language Models via Theorem Proving

Formal verification (FV) has witnessed growing significance with current emerging program synthesis by the evolving large language models (LLMs). However, current formal verification mainly resorts to symbolic verifiers or hand-craft rules, resulting in limitations for extensive and flexible verification. On the other hand, formal languages for automated theorem proving, such as Isabelle, as another line of rigorous verification, are maintained with comprehensive rules and theorems. In this paper, we propose FVEL, an interactive Formal Verification Environment with LLMs. Specifically, FVEL transforms a given code to be verified into Isabelle, and then conducts verification via neural automated theorem proving with an LLM. The joined paradigm leverages the rigorous yet abundant formulated and organized rules in Isabelle and is also convenient for introducing and adjusting cutting-edge LLMs. To achieve this goal, we extract a large-scale FVELER3. The FVELER dataset includes code dependencies and verification processes that are formulated in Isabelle, containing 758 theories, 29,125 lemmas, and 200,646 proof steps in total with in-depth dependencies. We benchmark FVELER in the FVEL environment by first fine-tuning LLMs with FVELER and then evaluating them on Code2Inv and SV-COMP. The results show that FVEL with FVELER fine-tuned Llama3- 8B solves 17.39% (69 -> 81) more problems, and Mistral-7B 12% (75 -> 84) more problems in SV-COMP. And the proportion of proof errors is reduced. Project page: https://fveler.github.io/.

ATG: Benchmarking Automated Theorem Generation for Generative Language Models

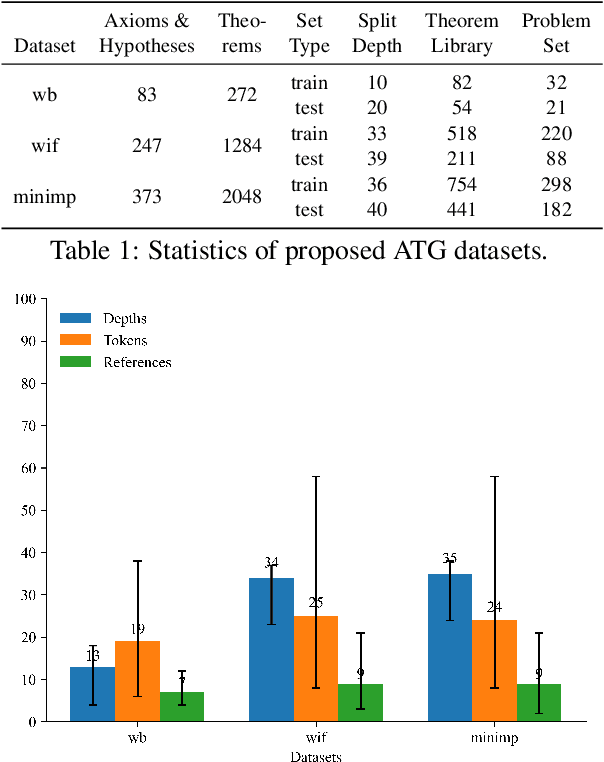
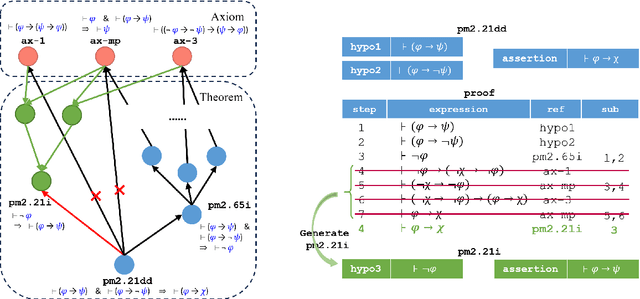
Humans can develop new theorems to explore broader and more complex mathematical results. While current generative language models (LMs) have achieved significant improvement in automatically proving theorems, their ability to generate new or reusable theorems is still under-explored. Without the new theorems, current LMs struggle to prove harder theorems that are distant from the given hypotheses with the exponentially growing search space. Therefore, this paper proposes an Automated Theorem Generation (ATG) benchmark that evaluates whether an agent can automatically generate valuable (and possibly brand new) theorems that are applicable for downstream theorem proving as reusable knowledge. Specifically, we construct the ATG benchmark by splitting the Metamath library into three sets: axioms, library, and problem based on their proving depth. We conduct extensive experiments to investigate whether current LMs can generate theorems in the library and benefit the problem theorems proving. The results demonstrate that high-quality ATG data facilitates models' performances on downstream ATP. However, there is still room for current LMs to develop better ATG and generate more advanced and human-like theorems. We hope the new ATG challenge can shed some light on advanced complex theorem proving.

MUSTARD: Mastering Uniform Synthesis of Theorem and Proof Data

Recent large language models (LLMs) have witnessed significant advancement in various tasks, including mathematical reasoning and theorem proving. As these two tasks require strict and formal multi-step inference, they are appealing domains for exploring the reasoning ability of LLMs but still face important challenges. Previous studies such as Chain-of-Thought (CoT) have revealed the effectiveness of intermediate steps guidance. However, such step-wise annotation requires heavy labor, leading to insufficient training steps for current benchmarks. To fill this gap, this work introduces MUSTARD, a data generation framework that masters uniform synthesis of theorem and proof data of high quality and diversity. MUSTARD synthesizes data in three stages: (1) It samples a few mathematical concept seeds as the problem category. (2) Then, it prompts a generative language model with the sampled concepts to obtain both the problems and their step-wise formal solutions. (3) Lastly, the framework utilizes a proof assistant (e.g., Lean Prover) to filter the valid proofs. With the proposed MUSTARD, we present a theorem-and-proof benchmark MUSTARDSAUCE with 5,866 valid data points. Each data point contains an informal statement, an informal proof, and a translated formal proof that passes the prover validation. We perform extensive analysis and demonstrate that MUSTARD generates validated high-quality step-by-step data. We further apply the MUSTARDSAUCE for fine-tuning smaller language models. The fine-tuned Llama 2-7B achieves a 15.41% average relative performance gain in automated theorem proving, and 8.18% in math word problems. Codes and data are available at https://github.com/Eleanor-H/MUSTARD.

TRIGO: Benchmarking Formal Mathematical Proof Reduction for Generative Language Models

Automated theorem proving (ATP) has become an appealing domain for exploring the reasoning ability of the recent successful generative language models. However, current ATP benchmarks mainly focus on symbolic inference, but rarely involve the understanding of complex number combination reasoning. In this work, we propose TRIGO, an ATP benchmark that not only requires a model to reduce a trigonometric expression with step-by-step proofs but also evaluates a generative LM's reasoning ability on formulas and its capability to manipulate, group, and factor number terms. We gather trigonometric expressions and their reduced forms from the web, annotate the simplification process manually, and translate it into the Lean formal language system. We then automatically generate additional examples from the annotated samples to expand the dataset. Furthermore, we develop an automatic generator based on Lean-Gym to create dataset splits of varying difficulties and distributions in order to thoroughly analyze the model's generalization ability. Our extensive experiments show our proposed TRIGO poses a new challenge for advanced generative LM's including GPT-4 which is pre-trained on a considerable amount of open-source formal theorem-proving language data, and provide a new tool to study the generative LM's ability on both formal and mathematical reasoning.

DQ-LoRe: Dual Queries with Low Rank Approximation Re-ranking for In-Context Learning

Recent advances in natural language processing, primarily propelled by Large Language Models (LLMs), have showcased their remarkable capabilities grounded in in-context learning. A promising avenue for guiding LLMs in intricate reasoning tasks involves the utilization of intermediate reasoning steps within the Chain-of-Thought (CoT) paradigm. Nevertheless, the central challenge lies in the effective selection of exemplars for facilitating in-context learning. In this study, we introduce a framework that leverages Dual Queries and Low-rank approximation Re-ranking (DQ-LoRe) to automatically select exemplars for in-context learning. Dual Queries first query LLM to obtain LLM-generated knowledge such as CoT, then query the retriever to obtain the final exemplars via both question and the knowledge. Moreover, for the second query, LoRe employs dimensionality reduction techniques to refine exemplar selection, ensuring close alignment with the input question's knowledge. Through extensive experiments, we demonstrate that DQ-LoRe significantly outperforms prior state-of-the-art methods in the automatic selection of exemplars for GPT-4, enhancing performance from 92.5% to 94.2%. Our comprehensive analysis further reveals that DQ-LoRe consistently outperforms retrieval-based approaches in terms of both performance and adaptability, especially in scenarios characterized by distribution shifts. DQ-LoRe pushes the boundaries of in-context learning and opens up new avenues for addressing complex reasoning challenges. We will release the code soon.

LEGO-Prover: Neural Theorem Proving with Growing Libraries

Despite the success of large language models (LLMs), the task of theorem proving still remains one of the hardest reasoning tasks that is far from being fully solved. Prior methods using language models have demonstrated promising results, but they still struggle to prove even middle school level theorems. One common limitation of these methods is that they assume a fixed theorem library during the whole theorem proving process. However, as we all know, creating new useful theorems or even new theories is not only helpful but crucial and necessary for advancing mathematics and proving harder and deeper results. In this work, we present LEGO-Prover, which employs a growing skill library containing verified lemmas as skills to augment the capability of LLMs used in theorem proving. By constructing the proof modularly, LEGO-Prover enables LLMs to utilize existing skills retrieved from the library and to create new skills during the proving process. These skills are further evolved (by prompting an LLM) to enrich the library on another scale. Modular and reusable skills are constantly added to the library to enable tackling increasingly intricate mathematical problems. Moreover, the learned library further bridges the gap between human proofs and formal proofs by making it easier to impute missing steps. LEGO-Prover advances the state-of-the-art pass rate on miniF2F-valid (48.0% to 57.0%) and miniF2F-test (45.5% to 47.1%). During the proving process, LEGO-Prover also manages to generate over 20,000 skills (theorems/lemmas) and adds them to the growing library. Our ablation study indicates that these newly added skills are indeed helpful for proving theorems, resulting in an improvement from a success rate of 47.1% to 50.4%. We also release our code and all the generated skills.

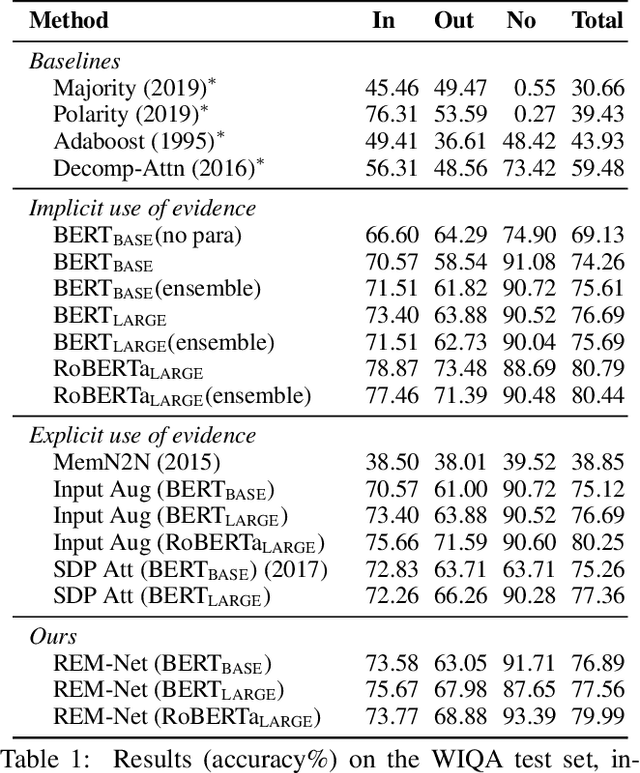
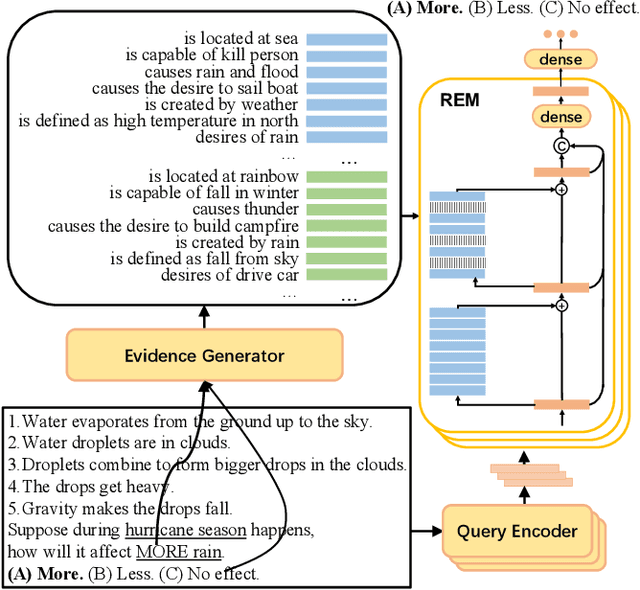
REM-Net: Recursive Erasure Memory Network for Commonsense Evidence Refinement

When answering a question, people often draw upon their rich world knowledge in addition to the particular context. While recent works retrieve supporting facts/evidence from commonsense knowledge bases to supply additional information to each question, there is still ample opportunity to advance it on the quality of the evidence. It is crucial since the quality of the evidence is the key to answering commonsense questions, and even determines the upper bound on the QA systems performance. In this paper, we propose a recursive erasure memory network (REM-Net) to cope with the quality improvement of evidence. To address this, REM-Net is equipped with a module to refine the evidence by recursively erasing the low-quality evidence that does not explain the question answering. Besides, instead of retrieving evidence from existing knowledge bases, REM-Net leverages a pre-trained generative model to generate candidate evidence customized for the question. We conduct experiments on two commonsense question answering datasets, WIQA and CosmosQA. The results demonstrate the performance of REM-Net and show that the refined evidence is explainable.

Knowledge-Routed Visual Question Reasoning: Challenges for Deep Representation Embedding

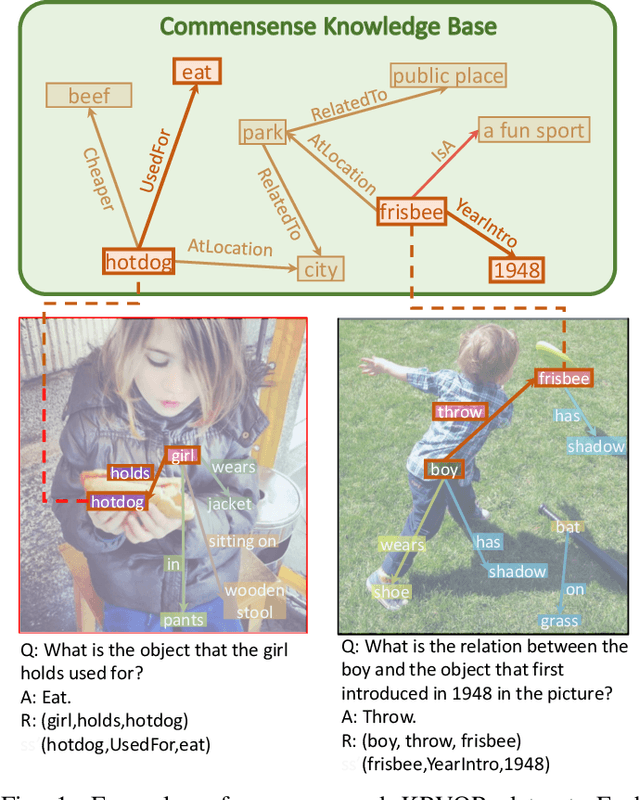
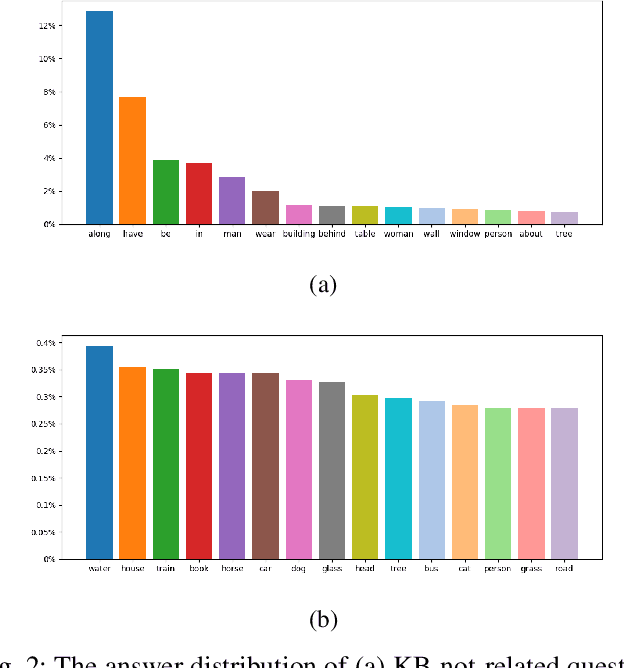
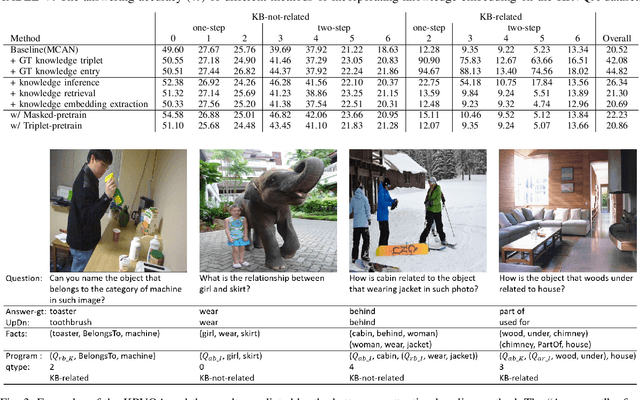
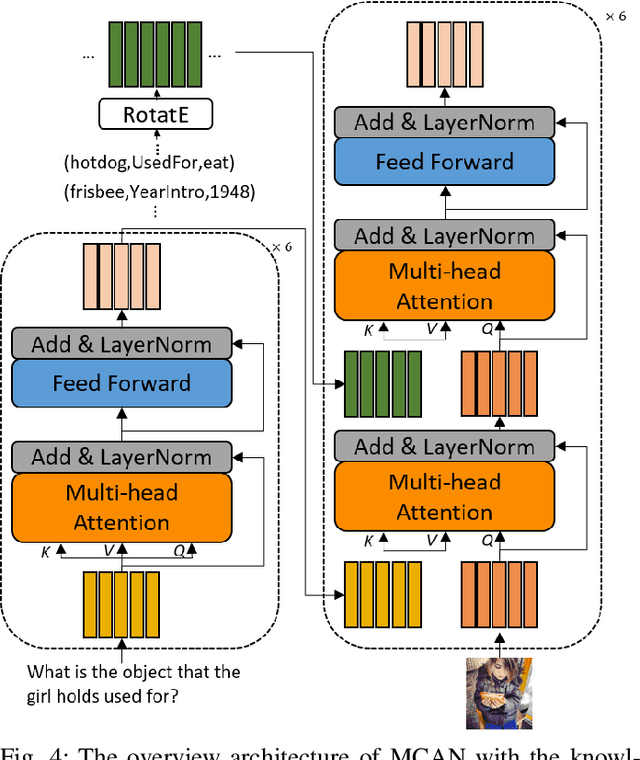
Though beneficial for encouraging the Visual Question Answering (VQA) models to discover the underlying knowledge by exploiting the input-output correlation beyond image and text contexts, the existing knowledge VQA datasets are mostly annotated in a crowdsource way, e.g., collecting questions and external reasons from different users via the internet. In addition to the challenge of knowledge reasoning, how to deal with the annotator bias also remains unsolved, which often leads to superficial over-fitted correlations between questions and answers. To address this issue, we propose a novel dataset named Knowledge-Routed Visual Question Reasoning for VQA model evaluation. Considering that a desirable VQA model should correctly perceive the image context, understand the question, and incorporate its learned knowledge, our proposed dataset aims to cutoff the shortcut learning exploited by the current deep embedding models and push the research boundary of the knowledge-based visual question reasoning. Specifically, we generate the question-answer pair based on both the Visual Genome scene graph and an external knowledge base with controlled programs to disentangle the knowledge from other biases. The programs can select one or two triplets from the scene graph or knowledge base to push multi-step reasoning, avoid answer ambiguity, and balanced the answer distribution. In contrast to the existing VQA datasets, we further imply the following two major constraints on the programs to incorporate knowledge reasoning: i) multiple knowledge triplets can be related to the question, but only one knowledge relates to the image object. This can enforce the VQA model to correctly perceive the image instead of guessing the knowledge based on the given question solely; ii) all questions are based on different knowledge, but the candidate answers are the same for both the training and test sets.

Linguistically Driven Graph Capsule Network for Visual Question Reasoning

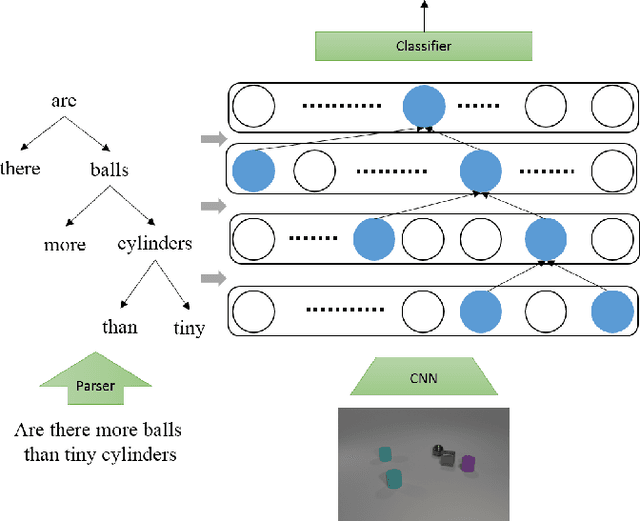
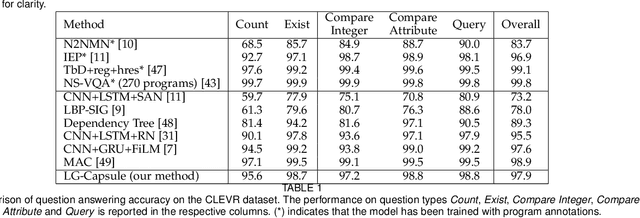
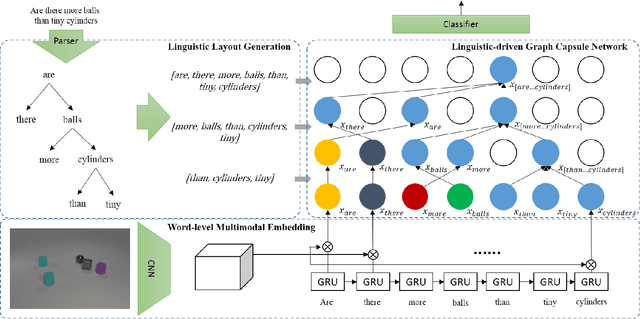
Recently, studies of visual question answering have explored various architectures of end-to-end networks and achieved promising results on both natural and synthetic datasets, which require explicitly compositional reasoning. However, it has been argued that these black-box approaches lack interpretability of results, and thus cannot perform well on generalization tasks due to overfitting the dataset bias. In this work, we aim to combine the benefits of both sides and overcome their limitations to achieve an end-to-end interpretable structural reasoning for general images without the requirement of layout annotations. Inspired by the property of a capsule network that can carve a tree structure inside a regular convolutional neural network (CNN), we propose a hierarchical compositional reasoning model called the "Linguistically driven Graph Capsule Network", where the compositional process is guided by the linguistic parse tree. Specifically, we bind each capsule in the lowest layer to bridge the linguistic embedding of a single word in the original question with visual evidence and then route them to the same capsule if they are siblings in the parse tree. This compositional process is achieved by performing inference on a linguistically driven conditional random field (CRF) and is performed across multiple graph capsule layers, which results in a compositional reasoning process inside a CNN. Experiments on the CLEVR dataset, CLEVR compositional generation test, and FigureQA dataset demonstrate the effectiveness and composition generalization ability of our end-to-end model.

Explainable High-order Visual Question Reasoning: A New Benchmark and Knowledge-routed Network

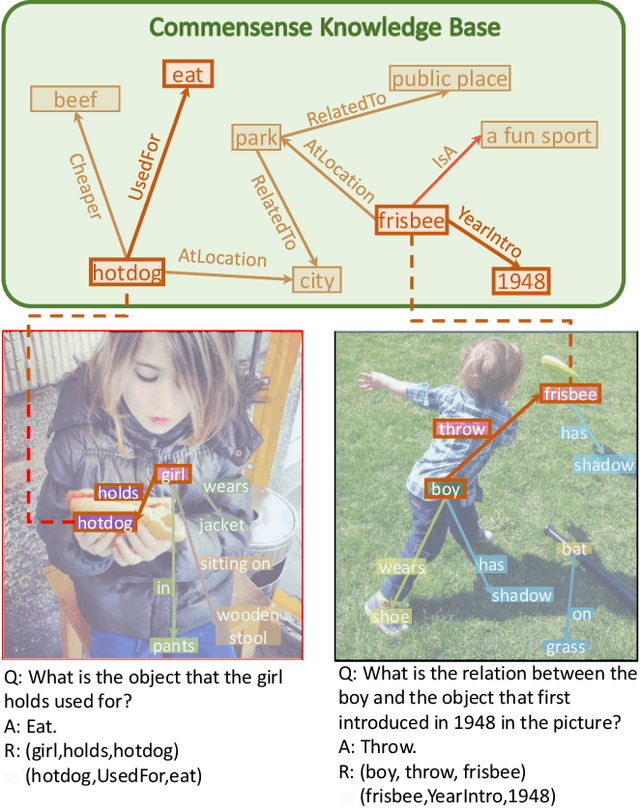
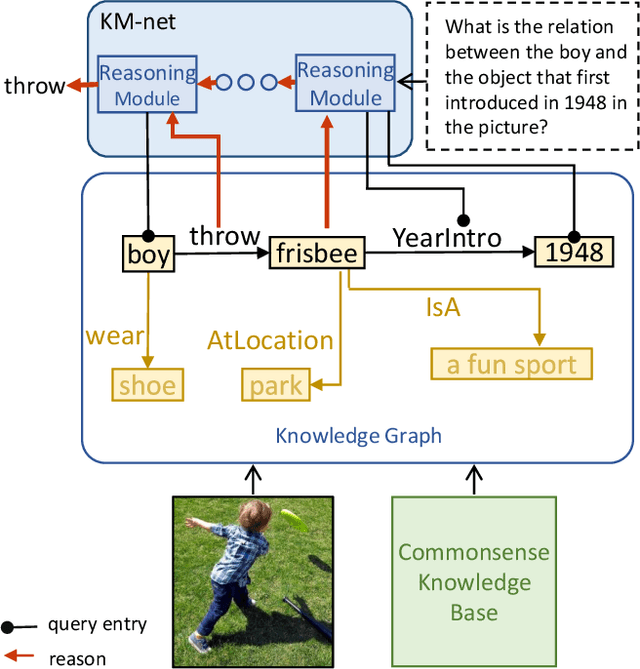
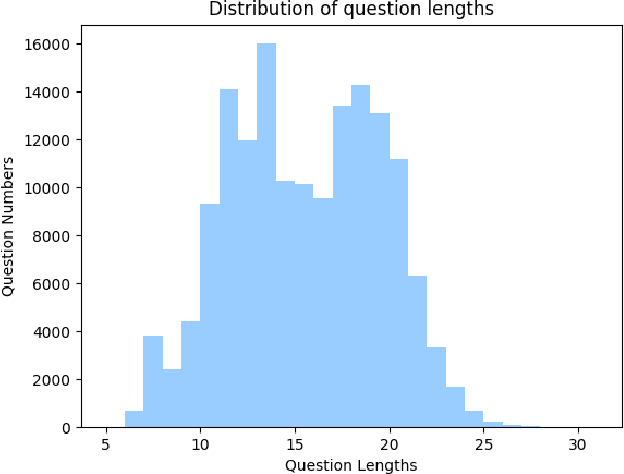
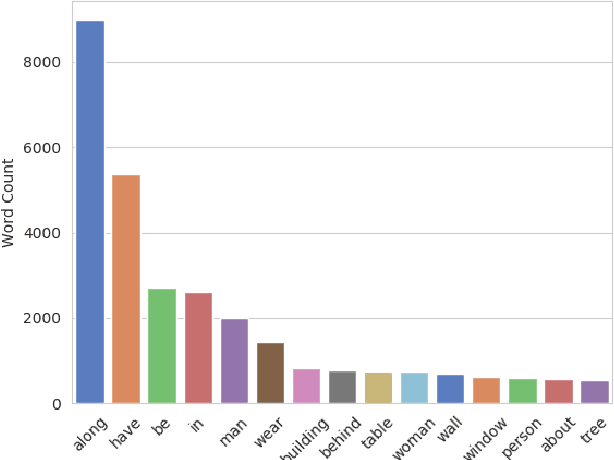
Explanation and high-order reasoning capabilities are crucial for real-world visual question answering with diverse levels of inference complexity (e.g., what is the dog that is near the girl playing with?) and important for users to understand and diagnose the trustworthiness of the system. Current VQA benchmarks on natural images with only an accuracy metric end up pushing the models to exploit the dataset biases and cannot provide any interpretable justification, which severally hinders advances in high-level question answering. In this work, we propose a new HVQR benchmark for evaluating explainable and high-order visual question reasoning ability with three distinguishable merits: 1) the questions often contain one or two relationship triplets, which requires the model to have the ability of multistep reasoning to predict plausible answers; 2) we provide an explicit evaluation on a multistep reasoning process that is constructed with image scene graphs and commonsense knowledge bases; and 3) each relationship triplet in a large-scale knowledge base only appears once among all questions, which poses challenges for existing networks that often attempt to overfit the knowledge base that already appears in the training set and enforces the models to handle unseen questions and knowledge fact usage. We also propose a new knowledge-routed modular network (KM-net) that incorporates the multistep reasoning process over a large knowledge base into visual question reasoning. An extensive dataset analysis and comparisons with existing models on the HVQR benchmark show that our benchmark provides explainable evaluations, comprehensive reasoning requirements and realistic challenges of VQA systems, as well as our KM-net's superiority in terms of accuracy and explanation ability.