Proving Theorems Recursively
Paper and Code
May 23, 2024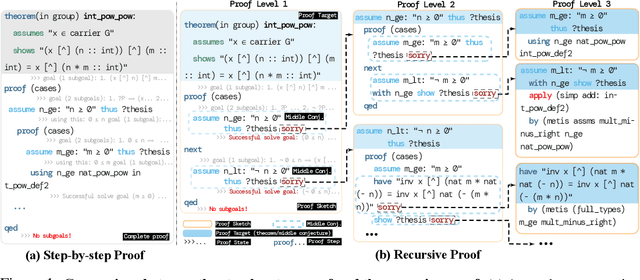

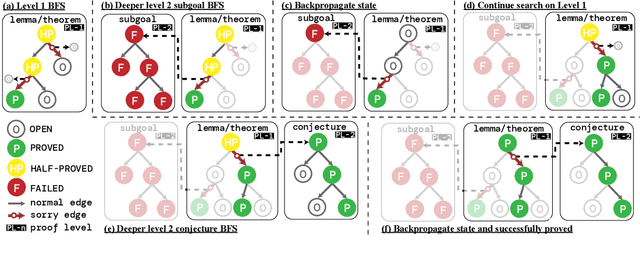
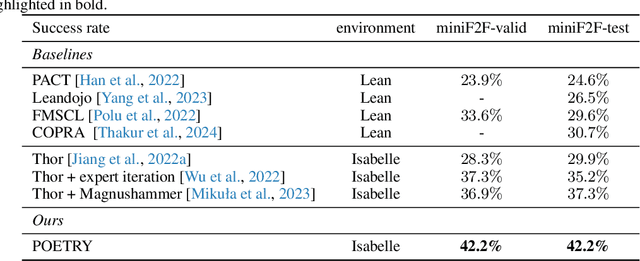
Recent advances in automated theorem proving leverages language models to explore expanded search spaces by step-by-step proof generation. However, such approaches are usually based on short-sighted heuristics (e.g., log probability or value function scores) that potentially lead to suboptimal or even distracting subgoals, preventing us from finding longer proofs. To address this challenge, we propose POETRY (PrOvE Theorems RecursivelY), which proves theorems in a recursive, level-by-level manner in the Isabelle theorem prover. Unlike previous step-by-step methods, POETRY searches for a verifiable sketch of the proof at each level and focuses on solving the current level's theorem or conjecture. Detailed proofs of intermediate conjectures within the sketch are temporarily replaced by a placeholder tactic called sorry, deferring their proofs to subsequent levels. This approach allows the theorem to be tackled incrementally by outlining the overall theorem at the first level and then solving the intermediate conjectures at deeper levels. Experiments are conducted on the miniF2F and PISA datasets and significant performance gains are observed in our POETRY approach over state-of-the-art methods. POETRY on miniF2F achieves an average proving success rate improvement of 5.1%. Moreover, we observe a substantial increase in the maximum proof length found by POETRY, from 10 to 26.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge