Markus N. Rabe
Spelling Bee Embeddings for Language Modeling
Jan 25, 2026Abstract:We introduce a simple modification to the embedding layer. The key change is to infuse token embeddings with information about their spelling. Models trained with these embeddings improve not only on spelling, but also across standard benchmarks. We conduct scaling studies for models with 40M to 800M parameters, which suggest that the improvements are equivalent to needing about 8% less compute and data to achieve the same test loss.
Baldur: Whole-Proof Generation and Repair with Large Language Models
Mar 16, 2023



Abstract:Formally verifying software properties is a highly desirable but labor-intensive task. Recent work has developed methods to automate formal verification using proof assistants, such as Coq and Isabelle/HOL, e.g., by training a model to predict one proof step at a time, and using that model to search through the space of possible proofs. This paper introduces a new method to automate formal verification: We use large language models, trained on natural language text and code and fine-tuned on proofs, to generate whole proofs for theorems at once, rather than one step at a time. We combine this proof generation model with a fine-tuned repair model to repair generated proofs, further increasing proving power. As its main contributions, this paper demonstrates for the first time that: (1) Whole-proof generation using transformers is possible and is as effective as search-based techniques without requiring costly search. (2) Giving the learned model additional context, such as a prior failed proof attempt and the ensuing error message, results in proof repair and further improves automated proof generation. (3) We establish a new state of the art for fully automated proof synthesis. We reify our method in a prototype, Baldur, and evaluate it on a benchmark of 6,336 Isabelle/HOL theorems and their proofs. In addition to empirically showing the effectiveness of whole-proof generation, repair, and added context, we show that Baldur improves on the state-of-the-art tool, Thor, by automatically generating proofs for an additional 8.7% of the theorems. Together, Baldur and Thor can prove 65.7% of the theorems fully automatically. This paper paves the way for new research into using large language models for automating formal verification.
Autoformalization with Large Language Models
May 25, 2022
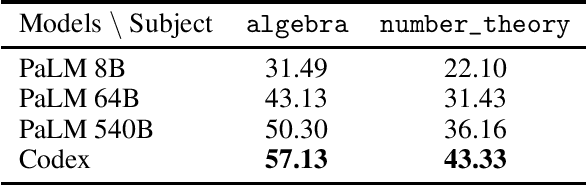


Abstract:Autoformalization is the process of automatically translating from natural language mathematics to formal specifications and proofs. A successful autoformalization system could advance the fields of formal verification, program synthesis, and artificial intelligence. While the long-term goal of autoformalization seemed elusive for a long time, we show large language models provide new prospects towards this goal. We make the surprising observation that LLMs can correctly translate a significant portion ($25.3\%$) of mathematical competition problems perfectly to formal specifications in Isabelle/HOL. We demonstrate the usefulness of this process by improving a previously introduced neural theorem prover via training on these autoformalized theorems. Our methodology results in a new state-of-the-art result on the MiniF2F theorem proving benchmark, improving the proof rate from $29.6\%$ to $35.2\%$.
Memorizing Transformers
Mar 16, 2022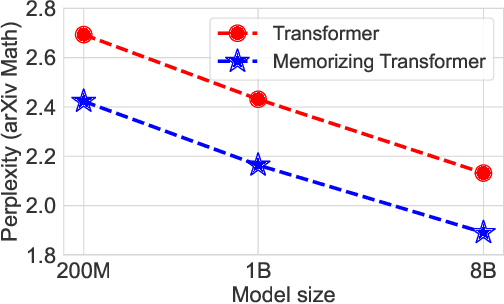
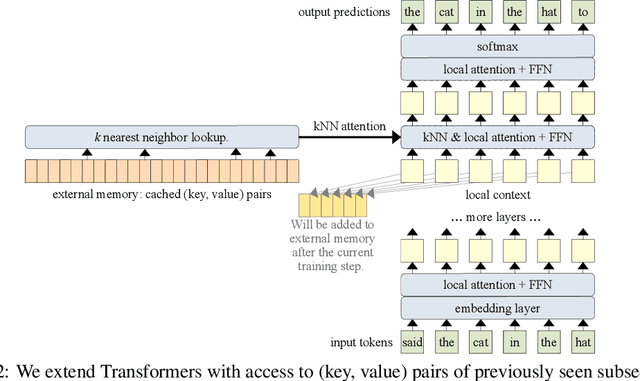

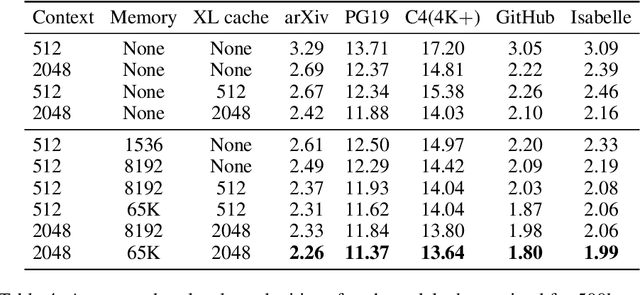
Abstract:Language models typically need to be trained or finetuned in order to acquire new knowledge, which involves updating their weights. We instead envision language models that can simply read and memorize new data at inference time, thus acquiring new knowledge immediately. In this work, we extend language models with the ability to memorize the internal representations of past inputs. We demonstrate that an approximate kNN lookup into a non-differentiable memory of recent (key, value) pairs improves language modeling across various benchmarks and tasks, including generic webtext (C4), math papers (arXiv), books (PG-19), code (Github), as well as formal theorems (Isabelle). We show that the performance steadily improves when we increase the size of memory up to 262K tokens. On benchmarks including code and mathematics, we find that the model is capable of making use of newly defined functions and theorems during test time.
Self-attention Does Not Need $O$ Memory
Dec 14, 2021



Abstract:We present a very simple algorithm for attention that requires $O(1)$ memory with respect to sequence length and an extension to self-attention that requires $O(\log n)$ memory. This is in contrast with the frequently stated belief that self-attention requires $O(n^2)$ memory. While the time complexity is still $O(n^2)$, device memory rather than compute capability is often the limiting factor on modern accelerators. Thus, reducing the memory requirements of attention allows processing of longer sequences than might otherwise be feasible. We provide a practical implementation for accelerators that requires $O(\sqrt{n})$ memory, is numerically stable, and is within a few percent of the runtime of the standard implementation of attention. We also demonstrate how to differentiate the function while remaining memory-efficient. For sequence length 16384, the memory overhead of self-attention is reduced by 59X for inference and by 32X for differentiation.
Neural Circuit Synthesis from Specification Patterns
Jul 25, 2021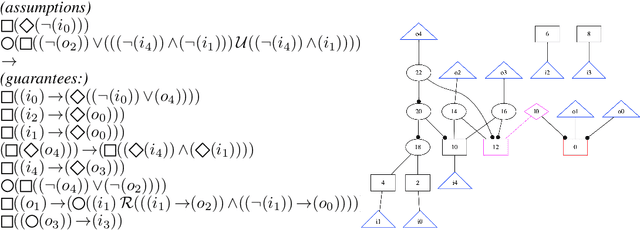


Abstract:We train hierarchical Transformers on the task of synthesizing hardware circuits directly out of high-level logical specifications in linear-time temporal logic (LTL). The LTL synthesis problem is a well-known algorithmic challenge with a long history and an annual competition is organized to track the improvement of algorithms and tooling over time. New approaches using machine learning might open a lot of possibilities in this area, but suffer from the lack of sufficient amounts of training data. In this paper, we consider a method to generate large amounts of additional training data, i.e., pairs of specifications and circuits implementing them. We ensure that this synthetic data is sufficiently close to human-written specifications by mining common patterns from the specifications used in the synthesis competitions. We show that hierarchical Transformers trained on this synthetic data solve a significant portion of problems from the synthesis competitions, and even out-of-distribution examples from a recent case study.
Language Modeling for Formal Mathematics
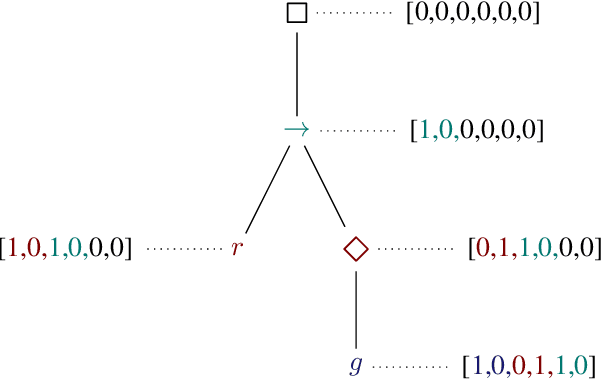
Jun 10, 2020
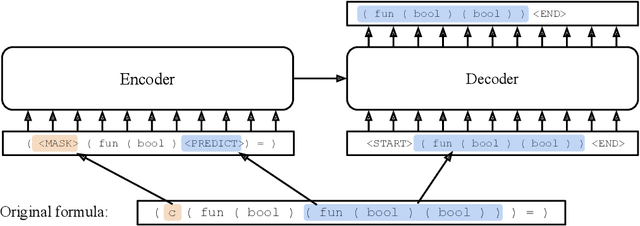
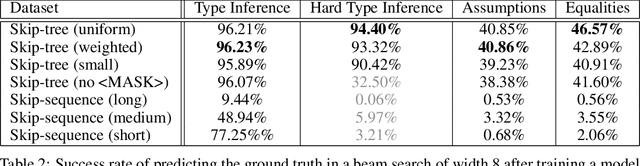
Abstract:We examine whether language modeling applied to mathematical formulas enables logical reasoning. We suggest several logical reasoning tasks that can be used to evaluate language models trained on formal mathematical statements, such as type inference, suggesting missing assumptions and completing equalities. To train language models for formal mathematics, we propose a novel skip-tree task, which outperforms standard language modeling tasks on our reasoning benchmarks. We also analyze the models' ability to formulate new conjectures by measuring how often the predictions that do not fit the ground truth or any training data turn out to be true and useful statements.
Teaching Temporal Logics to Neural Networks
Mar 06, 2020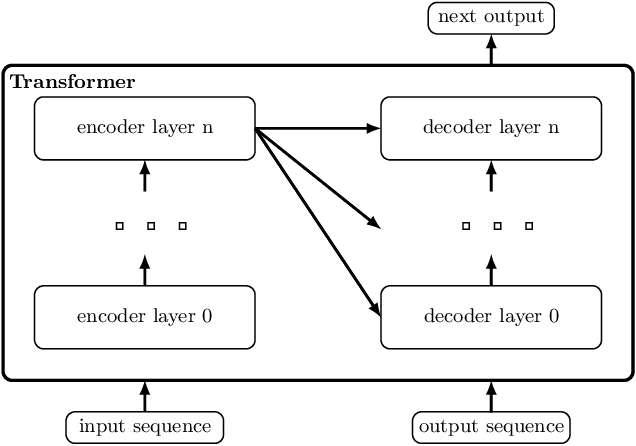
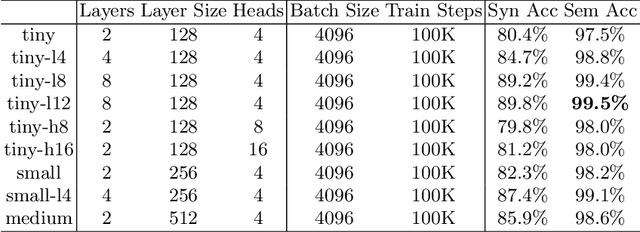
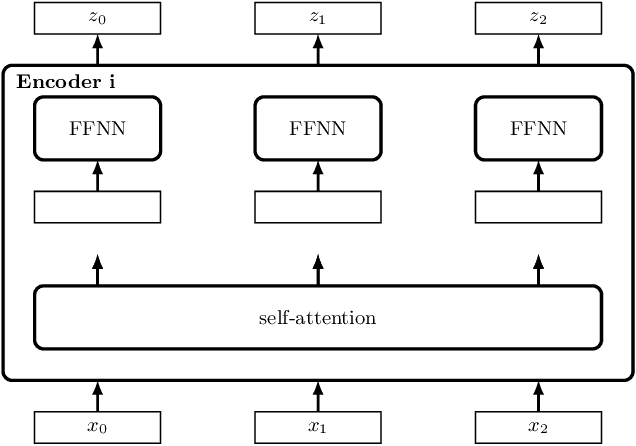
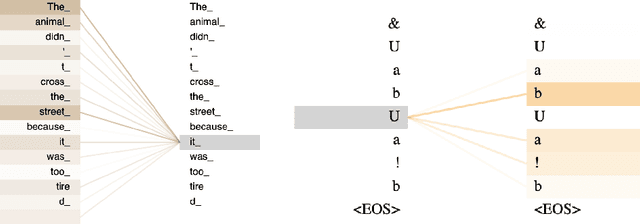
Abstract:We show that a deep neural network can learn the semantics of linear-time temporal logic (LTL). As a challenging task that requires deep understanding of the LTL semantics, we show that our network can solve the trace generation problem for LTL: given a satisfiable LTL formula, find a trace that satisfies the formula. We frame the trace generation problem for LTL as a translation task, i.e., to translate from formulas to satisfying traces, and train an off-the-shelf implementation of the Transformer, a recently introduced deep learning architecture proposed for solving natural language processing tasks. We provide a detailed analysis of our experimental results, comparing multiple hyperparameter settings and formula representations. After training for several hours on a single GPU the results were surprising: the Transformer returns the syntactically equivalent trace in 89% of the cases on a held-out test set. Most of the "mispredictions", however, (and overall more than 99% of the predicted traces) still satisfy the given LTL formula. In other words, the Transformer generalized from imperfect training data to the semantics of LTL.
Mathematical Reasoning in Latent Space
Sep 26, 2019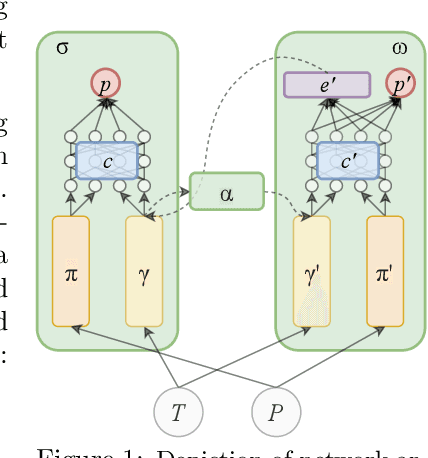
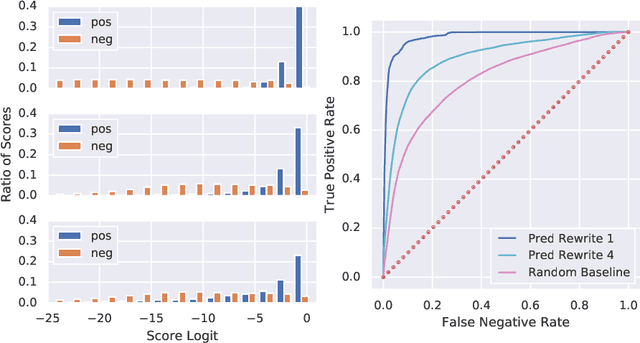
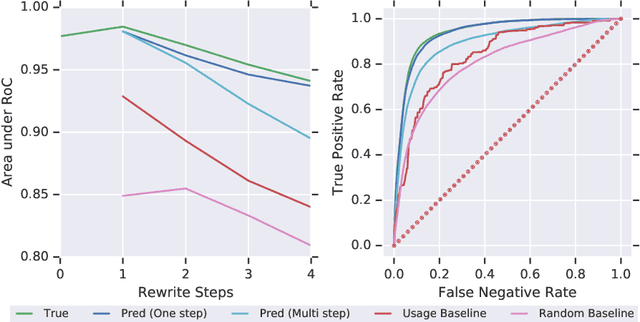
Abstract:We design and conduct a simple experiment to study whether neural networks can perform several steps of approximate reasoning in a fixed dimensional latent space. The set of rewrites (i.e. transformations) that can be successfully performed on a statement represents essential semantic features of the statement. We can compress this information by embedding the formula in a vector space, such that the vector associated with a statement can be used to predict whether a statement can be rewritten by other theorems. Predicting the embedding of a formula generated by some rewrite rule is naturally viewed as approximate reasoning in the latent space. In order to measure the effectiveness of this reasoning, we perform approximate deduction sequences in the latent space and use the resulting embedding to inform the semantic features of the corresponding formal statement (which is obtained by performing the corresponding rewrite sequence using real formulas). Our experiments show that graph neural networks can make non-trivial predictions about the rewrite-success of statements, even when they propagate predicted latent representations for several steps. Since our corpus of mathematical formulas includes a wide variety of mathematical disciplines, this experiment is a strong indicator for the feasibility of deduction in latent space in general.
Learning to Reason in Large Theories without Imitation
May 25, 2019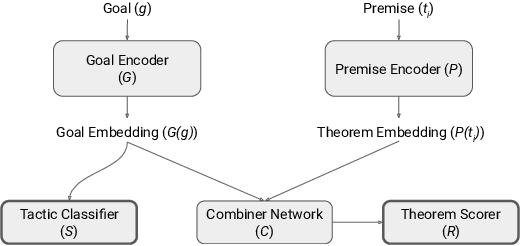

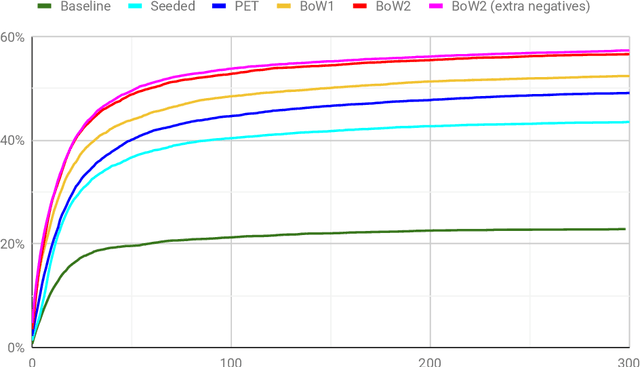

Abstract:Automated theorem proving in large theories can be learned via reinforcement learning over an indefinitely growing action space. In order to select actions, one performs nearest neighbor lookups in the knowledge base to find premises to be applied. Here we address the exploration for reinforcement learning in this space. Approaches (like epsilon-greedy strategy) that sample actions uniformly do not scale to this scenario as most actions lead to dead ends and unsuccessful proofs which are not useful for training our models. In this paper, we compare approaches that select premises using randomly initialized similarity measures and mixing them with the proposals of the learned model. We evaluate these on the HOList benchmark for tactics based higher order theorem proving. We implement an automated theorem prover named DeepHOL-Zero that does not use any of the human proofs and show that our improved exploration method manages to expand the training set continuously. DeepHOL-Zero outperforms the best theorem prover trained by imitation learning alone.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge