LIME: Learning Inductive Bias for Primitives of Mathematical Reasoning

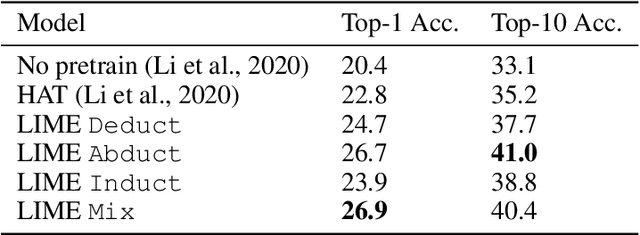
While designing inductive bias in neural architectures has been widely studied, we hypothesize that transformer networks are flexible enough to learn inductive bias from suitable generic tasks. Here, we replace architecture engineering by encoding inductive bias in the form of datasets. Inspired by Peirce's view that deduction, induction, and abduction form an irreducible set of reasoning primitives, we design three synthetic tasks that are intended to require the model to have these three abilities. We specifically design these synthetic tasks in a way that they are devoid of mathematical knowledge to ensure that only the fundamental reasoning biases can be learned from these tasks. This defines a new pre-training methodology called "LIME" (Learning Inductive bias for Mathematical rEasoning). Models trained with LIME significantly outperform vanilla transformers on three very different large mathematical reasoning benchmarks. Unlike dominating the computation cost as traditional pre-training approaches, LIME requires only a small fraction of the computation cost of the typical downstream task.

Graph Representations for Higher-Order Logic and Theorem Proving

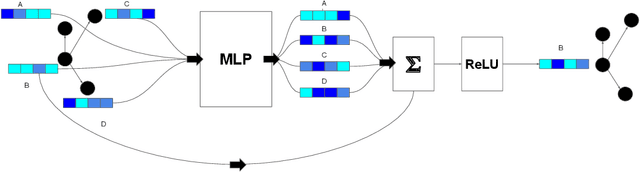
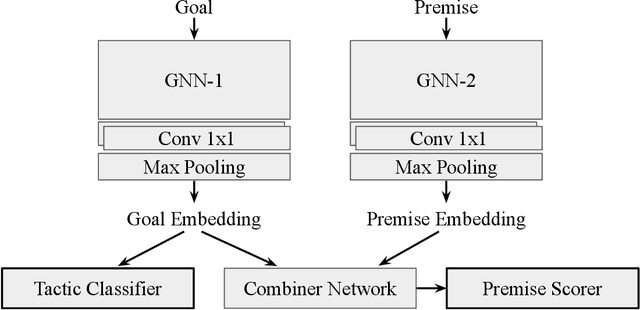
This paper presents the first use of graph neural networks (GNNs) for higher-order proof search and demonstrates that GNNs can improve upon state-of-the-art results in this domain. Interactive, higher-order theorem provers allow for the formalization of most mathematical theories and have been shown to pose a significant challenge for deep learning. Higher-order logic is highly expressive and, even though it is well-structured with a clearly defined grammar and semantics, there still remains no well-established method to convert formulas into graph-based representations. In this paper, we consider several graphical representations of higher-order logic and evaluate them against the HOList benchmark for higher-order theorem proving.