Sarah Loos
Graph Representations for Higher-Order Logic and Theorem Proving
May 24, 2019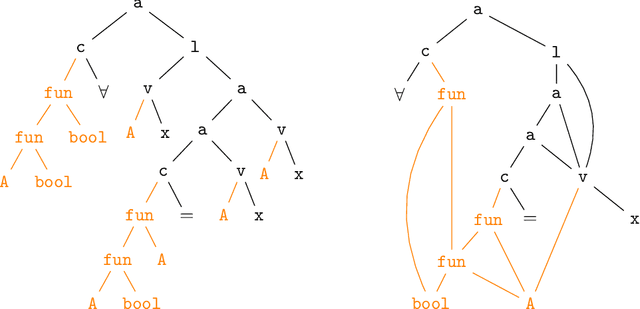
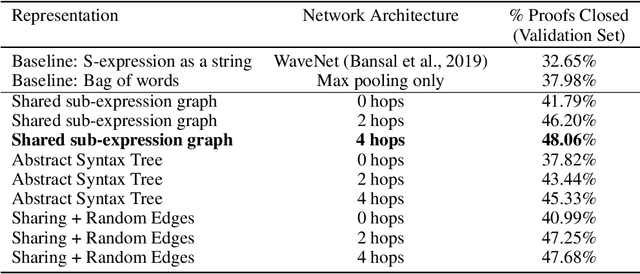
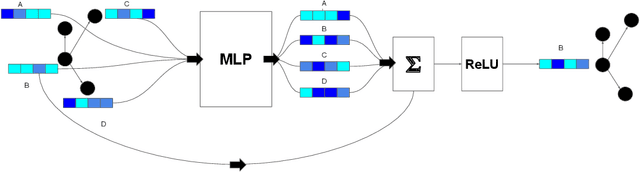
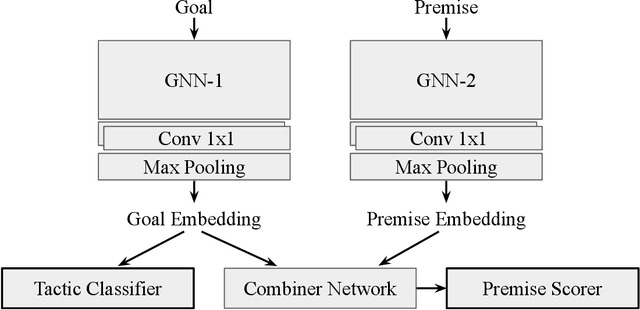
Abstract:This paper presents the first use of graph neural networks (GNNs) for higher-order proof search and demonstrates that GNNs can improve upon state-of-the-art results in this domain. Interactive, higher-order theorem provers allow for the formalization of most mathematical theories and have been shown to pose a significant challenge for deep learning. Higher-order logic is highly expressive and, even though it is well-structured with a clearly defined grammar and semantics, there still remains no well-established method to convert formulas into graph-based representations. In this paper, we consider several graphical representations of higher-order logic and evaluate them against the HOList benchmark for higher-order theorem proving.
Deep Network Guided Proof Search
Jan 24, 2017



Abstract:Deep learning techniques lie at the heart of several significant AI advances in recent years including object recognition and detection, image captioning, machine translation, speech recognition and synthesis, and playing the game of Go. Automated first-order theorem provers can aid in the formalization and verification of mathematical theorems and play a crucial role in program analysis, theory reasoning, security, interpolation, and system verification. Here we suggest deep learning based guidance in the proof search of the theorem prover E. We train and compare several deep neural network models on the traces of existing ATP proofs of Mizar statements and use them to select processed clauses during proof search. We give experimental evidence that with a hybrid, two-phase approach, deep learning based guidance can significantly reduce the average number of proof search steps while increasing the number of theorems proved. Using a few proof guidance strategies that leverage deep neural networks, we have found first-order proofs of 7.36% of the first-order logic translations of the Mizar Mathematical Library theorems that did not previously have ATP generated proofs. This increases the ratio of statements in the corpus with ATP generated proofs from 56% to 59%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge