PySCIPOpt-ML: Embedding Trained Machine Learning Models into Mixed-Integer Programs

A standard tool for modelling real-world optimisation problems is mixed-integer programming (MIP). However, for many of these problems there is either incomplete information describing variable relations, or the relations between variables are highly complex. To overcome both these hurdles, machine learning (ML) models are often used and embedded in the MIP as surrogate models to represent these relations. Due to the large amount of available ML frameworks, formulating ML models into MIPs is highly non-trivial. In this paper we propose a tool for the automatic MIP formulation of trained ML models, allowing easy integration of ML constraints into MIPs. In addition, we introduce a library of MIP instances with embedded ML constraints. The project is available at https://github.com/Opt-Mucca/PySCIPOpt-ML.

Adaptive Cut Selection in Mixed-Integer Linear Programming

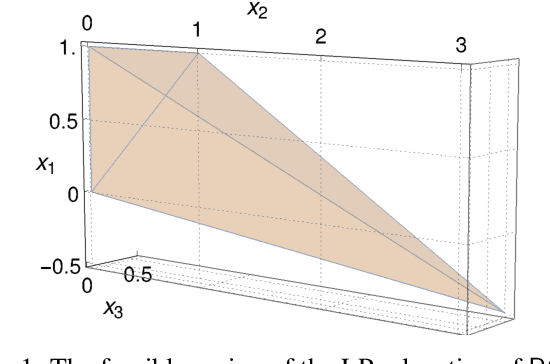
Cut selection is a subroutine used in all modern mixed-integer linear programming solvers with the goal of selecting a subset of generated cuts that induce optimal solver performance. These solvers have millions of parameter combinations, and so are excellent candidates for parameter tuning. Cut selection scoring rules are usually weighted sums of different measurements, where the weights are parameters. We present a parametric family of mixed-integer linear programs together with infinitely many family-wide valid cuts. Some of these cuts can induce integer optimal solutions directly after being applied, while others fail to do so even if an infinite amount are applied. We show for a specific cut selection rule, that any finite grid search of the parameter space will always miss all parameter values, which select integer optimal inducing cuts in an infinite amount of our problems. We propose a variation on the design of existing graph convolutional neural networks, adapting them to learn cut selection rule parameters. We present a reinforcement learning framework for selecting cuts, and train our design using said framework over MIPLIB 2017. Our framework and design show that adaptive cut selection does substantially improve performance over a diverse set of instances, but that finding a single function describing such a rule is difficult. Code for reproducing all experiments is available at https://github.com/Opt-Mucca/Adaptive-Cutsel-MILP.