PySCIPOpt-ML: Embedding Trained Machine Learning Models into Mixed-Integer Programs

A standard tool for modelling real-world optimisation problems is mixed-integer programming (MIP). However, for many of these problems there is either incomplete information describing variable relations, or the relations between variables are highly complex. To overcome both these hurdles, machine learning (ML) models are often used and embedded in the MIP as surrogate models to represent these relations. Due to the large amount of available ML frameworks, formulating ML models into MIPs is highly non-trivial. In this paper we propose a tool for the automatic MIP formulation of trained ML models, allowing easy integration of ML constraints into MIPs. In addition, we introduce a library of MIP instances with embedded ML constraints. The project is available at https://github.com/Opt-Mucca/PySCIPOpt-ML.

A Context-Aware Cutting Plane Selection Algorithm for Mixed-Integer Programming

The current cut selection algorithm used in mixed-integer programming solvers has remained largely unchanged since its creation. In this paper, we propose a set of new cut scoring measures, cut filtering techniques, and stopping criteria, extending the current state-of-the-art algorithm and obtaining a 5\% performance improvement for SCIP over the MIPLIB 2017 benchmark set.

Cutting Plane Selection with Analytic Centers and Multiregression

Cutting planes are a crucial component of state-of-the-art mixed-integer programming solvers, with the choice of which subset of cuts to add being vital for solver performance. We propose new distance-based measures to qualify the value of a cut by quantifying the extent to which it separates relevant parts of the relaxed feasible set. For this purpose, we use the analytic centers of the relaxation polytope or of its optimal face, as well as alternative optimal solutions of the linear programming relaxation. We assess the impact of the choice of distance measure on root node performance and throughout the whole branch-and-bound tree, comparing our measures against those prevalent in the literature. Finally, by a multi-output regression, we predict the relative performance of each measure, using static features readily available before the separation process. Our results indicate that analytic center-based methods help to significantly reduce the number of branch-and-bound nodes needed to explore the search space and that our multiregression approach can further improve on any individual method.

Adaptive Cut Selection in Mixed-Integer Linear Programming

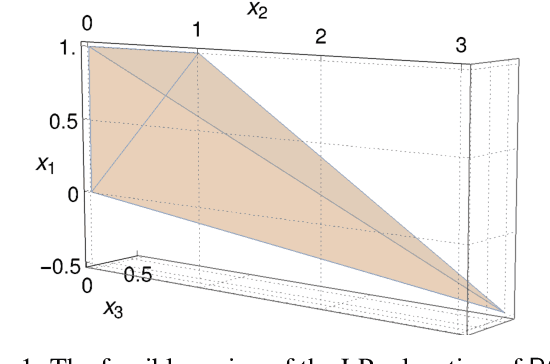
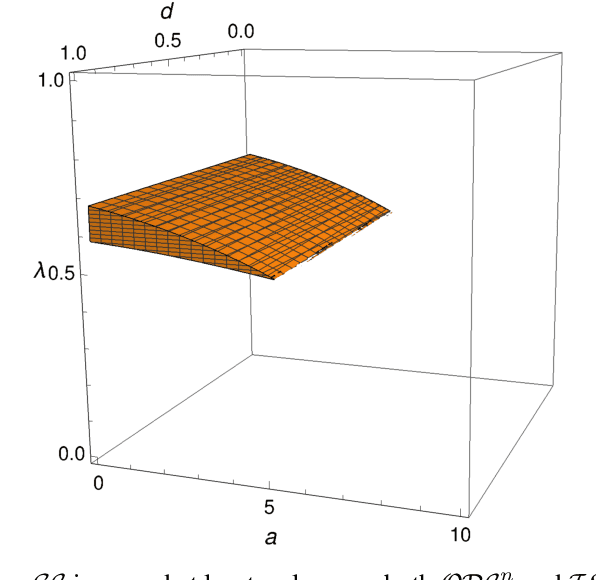
Cut selection is a subroutine used in all modern mixed-integer linear programming solvers with the goal of selecting a subset of generated cuts that induce optimal solver performance. These solvers have millions of parameter combinations, and so are excellent candidates for parameter tuning. Cut selection scoring rules are usually weighted sums of different measurements, where the weights are parameters. We present a parametric family of mixed-integer linear programs together with infinitely many family-wide valid cuts. Some of these cuts can induce integer optimal solutions directly after being applied, while others fail to do so even if an infinite amount are applied. We show for a specific cut selection rule, that any finite grid search of the parameter space will always miss all parameter values, which select integer optimal inducing cuts in an infinite amount of our problems. We propose a variation on the design of existing graph convolutional neural networks, adapting them to learn cut selection rule parameters. We present a reinforcement learning framework for selecting cuts, and train our design using said framework over MIPLIB 2017. Our framework and design show that adaptive cut selection does substantially improve performance over a diverse set of instances, but that finding a single function describing such a rule is difficult. Code for reproducing all experiments is available at https://github.com/Opt-Mucca/Adaptive-Cutsel-MILP.

Generative deep learning for decision making in gas networks

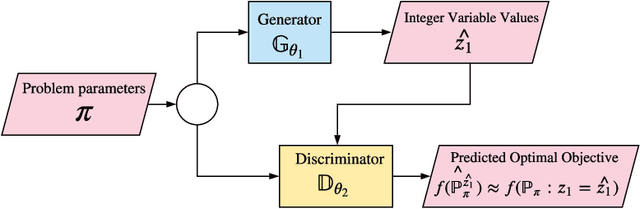
A decision support system relies on frequent re-solving of similar problem instances. While the general structure remains the same in corresponding applications, the input parameters are updated on a regular basis. We propose a generative neural network design for learning integer decision variables of mixed-integer linear programming (MILP) formulations of these problems. We utilise a deep neural network discriminator and a MILP solver as our oracle to train our generative neural network. In this article, we present the results of our design applied to the transient gas optimisation problem. With the trained network we produce a feasible solution in 2.5s, use it as a warm-start solution, and thereby decrease global optimal solution solve time by 60.5%.