A Context-Aware Cutting Plane Selection Algorithm for Mixed-Integer Programming

The current cut selection algorithm used in mixed-integer programming solvers has remained largely unchanged since its creation. In this paper, we propose a set of new cut scoring measures, cut filtering techniques, and stopping criteria, extending the current state-of-the-art algorithm and obtaining a 5\% performance improvement for SCIP over the MIPLIB 2017 benchmark set.

Cutting Plane Selection with Analytic Centers and Multiregression

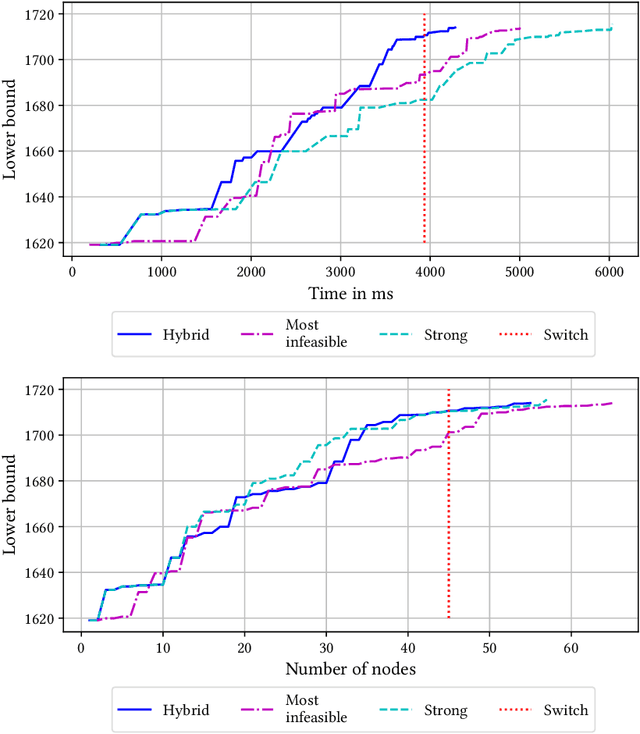
Cutting planes are a crucial component of state-of-the-art mixed-integer programming solvers, with the choice of which subset of cuts to add being vital for solver performance. We propose new distance-based measures to qualify the value of a cut by quantifying the extent to which it separates relevant parts of the relaxed feasible set. For this purpose, we use the analytic centers of the relaxation polytope or of its optimal face, as well as alternative optimal solutions of the linear programming relaxation. We assess the impact of the choice of distance measure on root node performance and throughout the whole branch-and-bound tree, comparing our measures against those prevalent in the literature. Finally, by a multi-output regression, we predict the relative performance of each measure, using static features readily available before the separation process. Our results indicate that analytic center-based methods help to significantly reduce the number of branch-and-bound nodes needed to explore the search space and that our multiregression approach can further improve on any individual method.

Convex integer optimization with Frank-Wolfe methods

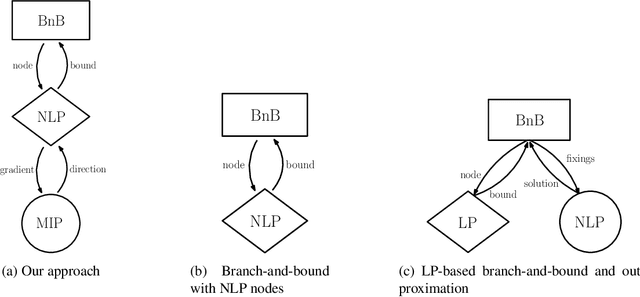
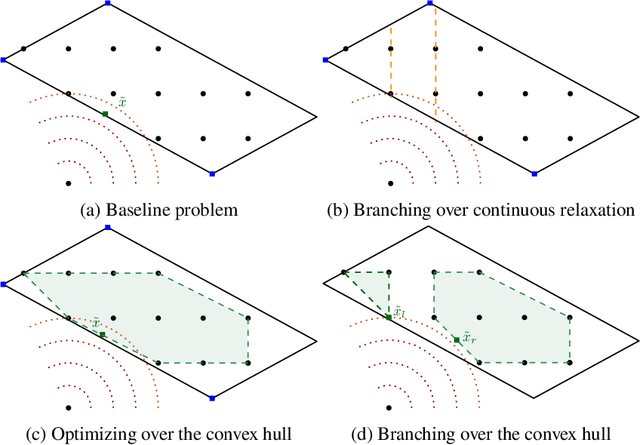
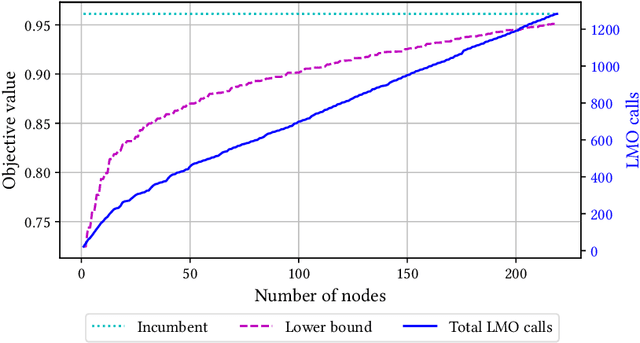
Mixed-integer nonlinear optimization is a broad class of problems that feature combinatorial structures and nonlinearities. Typical exact methods combine a branch-and-bound scheme with relaxation and separation subroutines. We investigate the properties and advantages of error-adaptive first-order methods based on the Frank-Wolfe algorithm for this setting, requiring only a gradient oracle for the objective function and linear optimization over the feasible set. In particular, we will study the algorithmic consequences of optimizing with a branch-and-bound approach where the subproblem is solved over the convex hull of the mixed-integer feasible set thanks to linear oracle calls, compared to solving the subproblems over the continuous relaxation of the same set. This novel approach computes feasible solutions while working on a single representation of the polyhedral constraints, leveraging the full extent of Mixed-Integer Programming (MIP) solvers without an outer approximation scheme.

Flexible Differentiable Optimization via Model Transformations

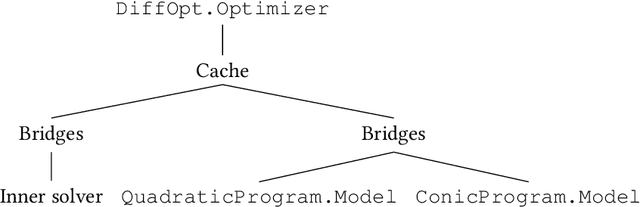
We introduce DiffOpt.jl, a Julia library to differentiate through the solution of convex optimization problems with respect to arbitrary parameters present in the objective and/or constraints. The library builds upon MathOptInterface, thus leveraging the rich ecosystem of solvers and composing well with modelling languages like JuMP. DiffOpt offers both forward and reverse differentiation modes, enabling multiple use cases from hyperparameter optimization to backpropagation and sensitivity analysis, bridging constrained optimization with end-to-end differentiable programming.

Interpretable Neural Networks with Frank-Wolfe: Sparse Relevance Maps and Relevance Orderings

We study the effects of constrained optimization formulations and Frank-Wolfe algorithms for obtaining interpretable neural network predictions. Reformulating the Rate-Distortion Explanations (RDE) method for relevance attribution as a constrained optimization problem provides precise control over the sparsity of relevance maps. This enables a novel multi-rate as well as a relevance-ordering variant of RDE that both empirically outperform standard RDE in a well-established comparison test. We showcase several deterministic and stochastic variants of the Frank-Wolfe algorithm and their effectiveness for RDE.

Simple steps are all you need: Frank-Wolfe and generalized self-concordant functions

Generalized self-concordance is a key property present in the objective function of many important learning problems. We establish the convergence rate of a simple Frank-Wolfe variant that uses the open-loop step size strategy $\gamma_t = 2/(t+2)$, obtaining a $\mathcal{O}(1/t)$ convergence rate for this class of functions in terms of primal gap and Frank-Wolfe gap, where $t$ is the iteration count. This avoids the use of second-order information or the need to estimate local smoothness parameters of previous work. We also show improved convergence rates for various common cases, e.g., when the feasible region under consideration is uniformly convex or polyhedral.