Meta-learning For Few-Shot Time Series Crop Type Classification: A Benchmark On The EuroCropsML Dataset

Spatial imbalances in crop type data pose significant challenges for accurate classification in remote sensing applications. Algorithms aiming at transferring knowledge from data-rich to data-scarce tasks have thus surged in popularity. However, despite their effectiveness in previous evaluations, their performance in challenging real-world applications is unclear and needs to be evaluated. This study benchmarks transfer learning and several meta-learning algorithms, including (First-Order) Model-Agnostic Meta-Learning ((FO)-MAML), Almost No Inner Loop (ANIL), and Task-Informed Meta-Learning (TIML), on the real-world EuroCropsML time series dataset, which combines farmer-reported crop data with Sentinel-2 satellite observations from Estonia, Latvia, and Portugal. Our findings indicate that MAML-based meta-learning algorithms achieve slightly higher accuracy compared to simpler transfer learning methods when applied to crop type classification tasks in Estonia after pre-training on data from Latvia. However, this improvement comes at the cost of increased computational demands and training time. Moreover, we find that the transfer of knowledge between geographically disparate regions, such as Estonia and Portugal, poses significant challenges to all investigated algorithms. These insights underscore the trade-offs between accuracy and computational resource requirements in selecting machine learning methods for real-world crop type classification tasks and highlight the difficulties of transferring knowledge between different regions of the Earth. To facilitate future research in this domain, we present the first comprehensive benchmark for evaluating transfer and meta-learning methods for crop type classification under real-world conditions. The corresponding code is publicly available at https://github.com/dida-do/eurocrops-meta-learning.

EuroCropsML: A Time Series Benchmark Dataset For Few-Shot Crop Type Classification

We introduce EuroCropsML, an analysis-ready remote sensing machine learning dataset for time series crop type classification of agricultural parcels in Europe. It is the first dataset designed to benchmark transnational few-shot crop type classification algorithms that supports advancements in algorithmic development and research comparability. It comprises 706 683 multi-class labeled data points across 176 classes, featuring annual time series of per-parcel median pixel values from Sentinel-2 L1C data for 2021, along with crop type labels and spatial coordinates. Based on the open-source EuroCrops collection, EuroCropsML is publicly available on Zenodo.

Let's Enhance: A Deep Learning Approach to Extreme Deblurring of Text Images

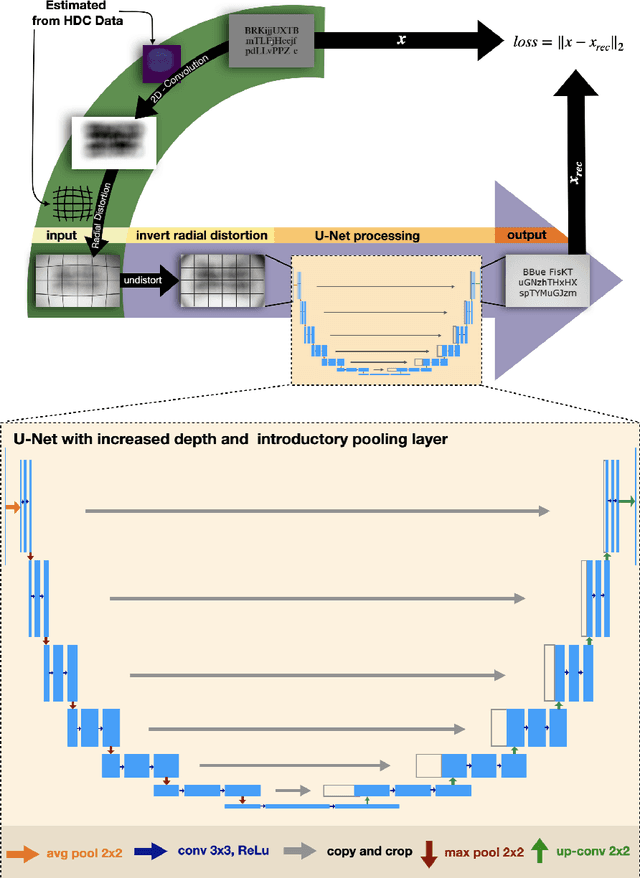
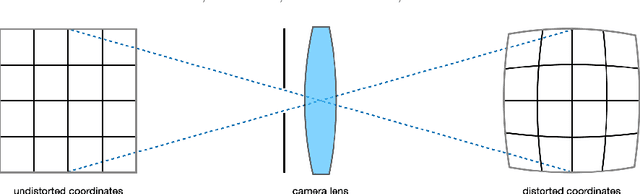
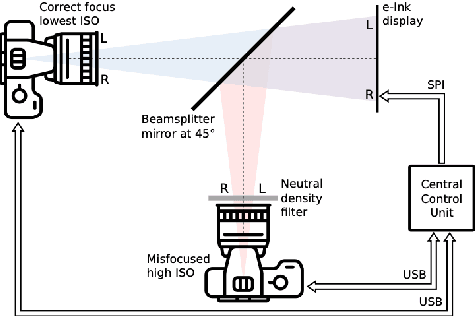
This work presents a novel deep-learning-based pipeline for the inverse problem of image deblurring, leveraging augmentation and pre-training with synthetic data. Our results build on our winning submission to the recent Helsinki Deblur Challenge 2021, whose goal was to explore the limits of state-of-the-art deblurring algorithms in a real-world data setting. The task of the challenge was to deblur out-of-focus images of random text, thereby in a downstream task, maximizing an optical-character-recognition-based score function. A key step of our solution is the data-driven estimation of the physical forward model describing the blur process. This enables a stream of synthetic data, generating pairs of ground-truth and blurry images on-the-fly, which is used for an extensive augmentation of the small amount of challenge data provided. The actual deblurring pipeline consists of an approximate inversion of the radial lens distortion (determined by the estimated forward model) and a U-Net architecture, which is trained end-to-end. Our algorithm was the only one passing the hardest challenge level, achieving over 70% character recognition accuracy. Our findings are well in line with the paradigm of data-centric machine learning, and we demonstrate its effectiveness in the context of inverse problems. Apart from a detailed presentation of our methodology, we also analyze the importance of several design choices in a series of ablation studies. The code of our challenge submission is available under https://github.com/theophil-trippe/HDC_TUBerlin_version_1.

Near-Exact Recovery for Tomographic Inverse Problems via Deep Learning

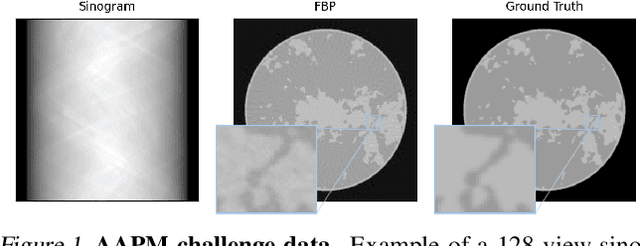
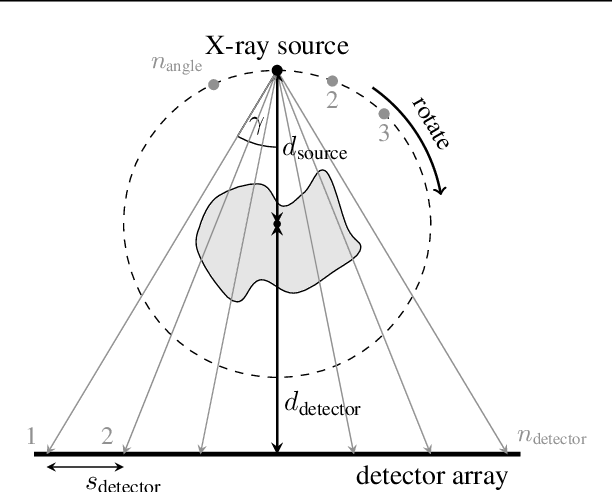
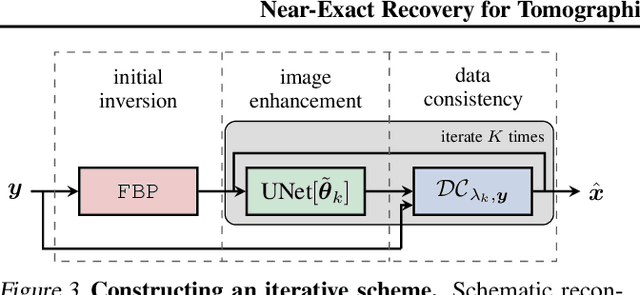
This work is concerned with the following fundamental question in scientific machine learning: Can deep-learning-based methods solve noise-free inverse problems to near-perfect accuracy? Positive evidence is provided for the first time, focusing on a prototypical computed tomography (CT) setup. We demonstrate that an iterative end-to-end network scheme enables reconstructions close to numerical precision, comparable to classical compressed sensing strategies. Our results build on our winning submission to the recent AAPM DL-Sparse-View CT Challenge. Its goal was to identify the state-of-the-art in solving the sparse-view CT inverse problem with data-driven techniques. A specific difficulty of the challenge setup was that the precise forward model remained unknown to the participants. Therefore, a key feature of our approach was to initially estimate the unknown fanbeam geometry in a data-driven calibration step. Apart from an in-depth analysis of our methodology, we also demonstrate its state-of-the-art performance on the open-access real-world dataset LoDoPaB CT.

A Complete Characterisation of ReLU-Invariant Distributions

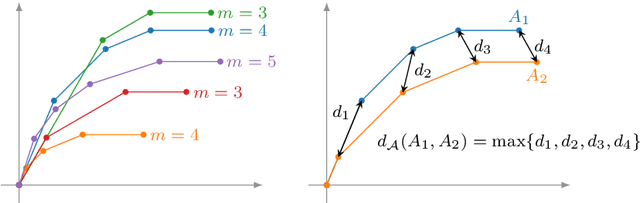
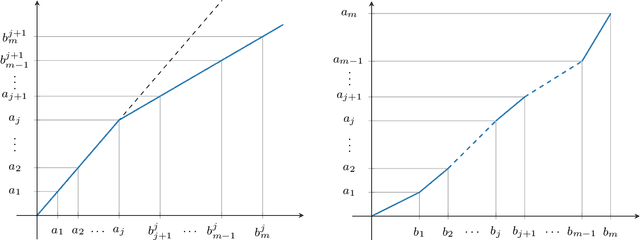
We give a complete characterisation of families of probability distributions that are invariant under the action of ReLU neural network layers. The need for such families arises during the training of Bayesian networks or the analysis of trained neural networks, e.g., in the context of uncertainty quantification (UQ) or explainable artificial intelligence (XAI). We prove that no invariant parametrised family of distributions can exist unless at least one of the following three restrictions holds: First, the network layers have a width of one, which is unreasonable for practical neural networks. Second, the probability measures in the family have finite support, which basically amounts to sampling distributions. Third, the parametrisation of the family is not locally Lipschitz continuous, which excludes all computationally feasible families. Finally, we show that these restrictions are individually necessary. For each of the three cases we can construct an invariant family exploiting exactly one of the restrictions but not the other two.

Interpretable Neural Networks with Frank-Wolfe: Sparse Relevance Maps and Relevance Orderings

We study the effects of constrained optimization formulations and Frank-Wolfe algorithms for obtaining interpretable neural network predictions. Reformulating the Rate-Distortion Explanations (RDE) method for relevance attribution as a constrained optimization problem provides precise control over the sparsity of relevance maps. This enables a novel multi-rate as well as a relevance-ordering variant of RDE that both empirically outperform standard RDE in a well-established comparison test. We showcase several deterministic and stochastic variants of the Frank-Wolfe algorithm and their effectiveness for RDE.

AAPM DL-Sparse-View CT Challenge Submission Report: Designing an Iterative Network for Fanbeam-CT with Unknown Geometry

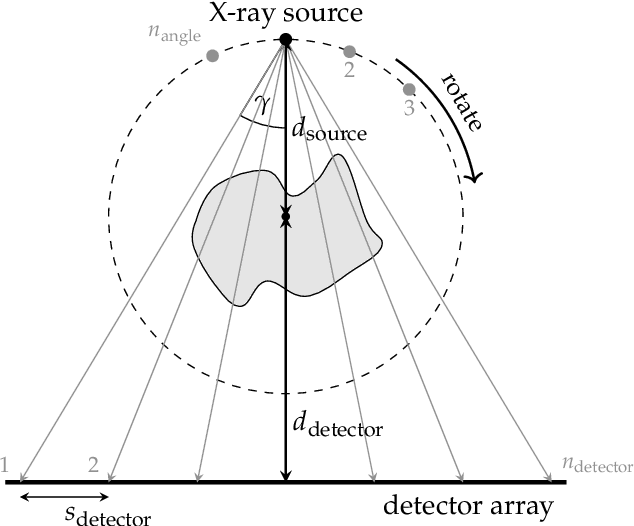
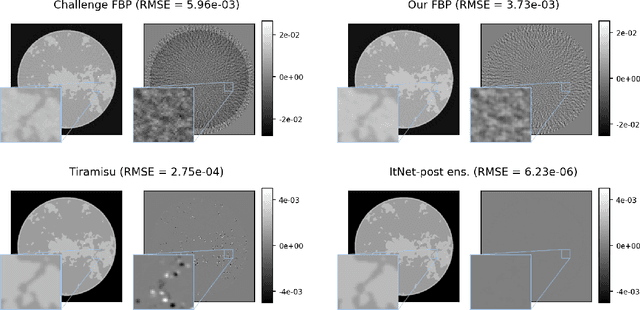
This report is dedicated to a short motivation and description of our contribution to the AAPM DL-Sparse-View CT Challenge (team name: "robust-and-stable"). The task is to recover breast model phantom images from limited view fanbeam measurements using data-driven reconstruction techniques. The challenge is distinctive in the sense that participants are provided with a collection of ground truth images and their noiseless, subsampled sinograms (as well as the associated limited view filtered backprojection images), but not with the actual forward model. Therefore, our approach first estimates the fanbeam geometry in a data-driven geometric calibration step. In a subsequent two-step procedure, we design an iterative end-to-end network that enables the computation of near-exact solutions.

Solving Inverse Problems With Deep Neural Networks -- Robustness Included?

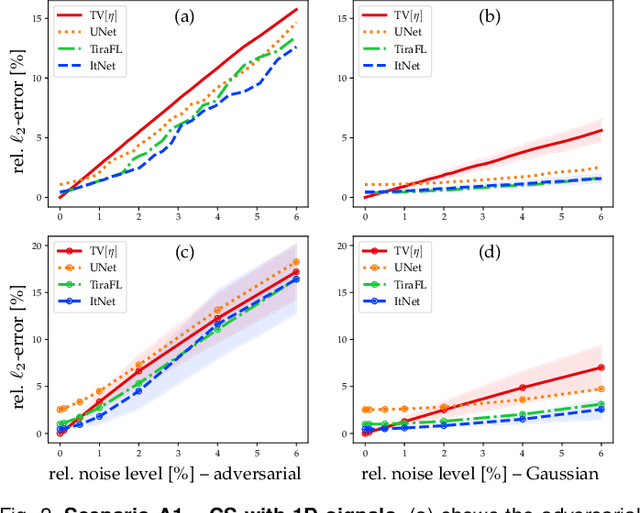
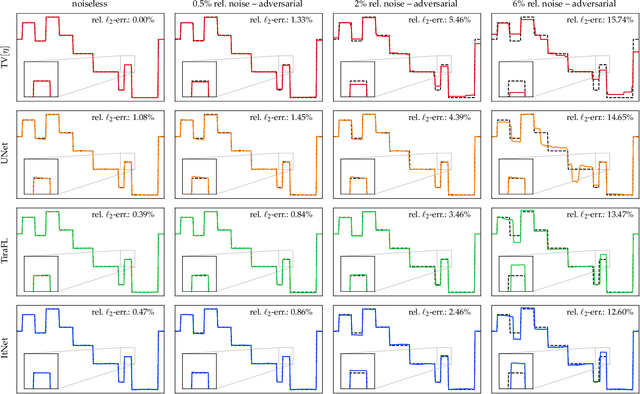
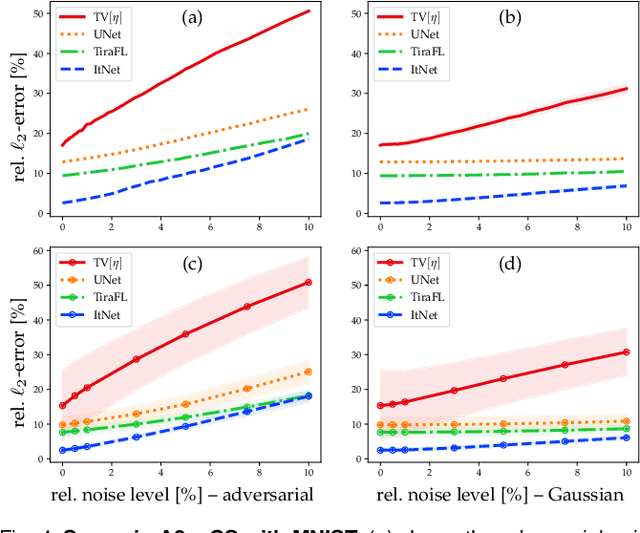
In the past five years, deep learning methods have become state-of-the-art in solving various inverse problems. Before such approaches can find application in safety-critical fields, a verification of their reliability appears mandatory. Recent works have pointed out instabilities of deep neural networks for several image reconstruction tasks. In analogy to adversarial attacks in classification, it was shown that slight distortions in the input domain may cause severe artifacts. The present article sheds new light on this concern, by conducting an extensive study of the robustness of deep-learning-based algorithms for solving underdetermined inverse problems. This covers compressed sensing with Gaussian measurements as well as image recovery from Fourier and Radon measurements, including a real-world scenario for magnetic resonance imaging (using the NYU-fastMRI dataset). Our main focus is on computing adversarial perturbations of the measurements that maximize the reconstruction error. A distinctive feature of our approach is the quantitative and qualitative comparison with total-variation minimization, which serves as a provably robust reference method. In contrast to previous findings, our results reveal that standard end-to-end network architectures are not only resilient against statistical noise, but also against adversarial perturbations. All considered networks are trained by common deep learning techniques, without sophisticated defense strategies.

Interval Neural Networks as Instability Detectors for Image Reconstructions

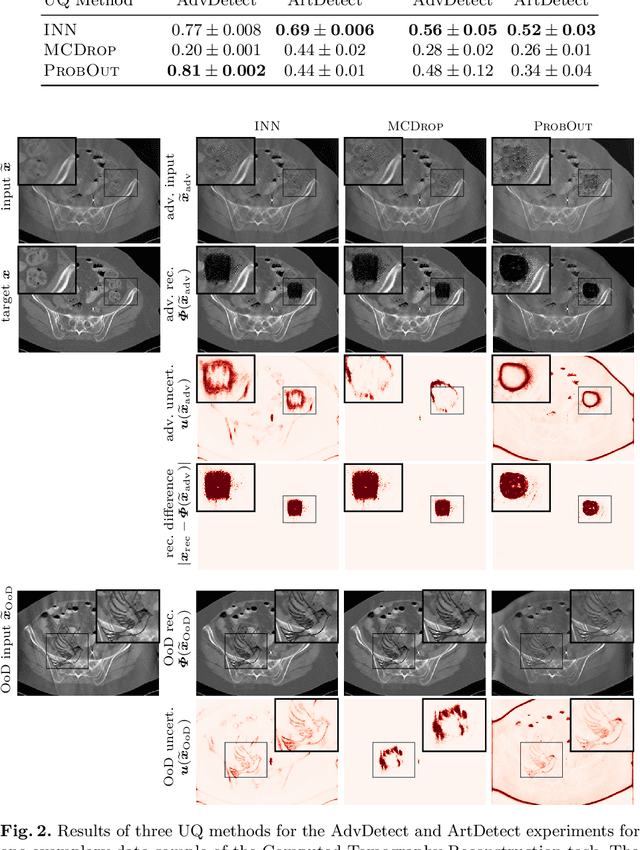
This work investigates the detection of instabilities that may occur when utilizing deep learning models for image reconstruction tasks. Although neural networks often empirically outperform traditional reconstruction methods, their usage for sensitive medical applications remains controversial. Indeed, in a recent series of works, it has been demonstrated that deep learning approaches are susceptible to various types of instabilities, caused for instance by adversarial noise or out-of-distribution features. It is argued that this phenomenon can be observed regardless of the underlying architecture and that there is no easy remedy. Based on this insight, the present work demonstrates on two use cases how uncertainty quantification methods can be employed as instability detectors. In particular, it is shown that the recently proposed Interval Neural Networks are highly effective in revealing instabilities of reconstructions. Such an ability is crucial to ensure a safe use of deep learning-based methods for medical image reconstruction.

Interval Neural Networks: Uncertainty Scores

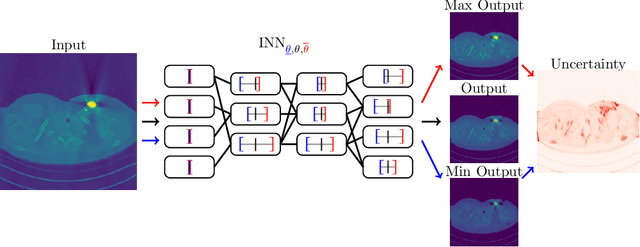
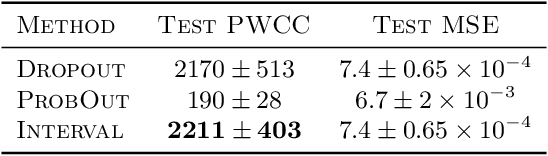
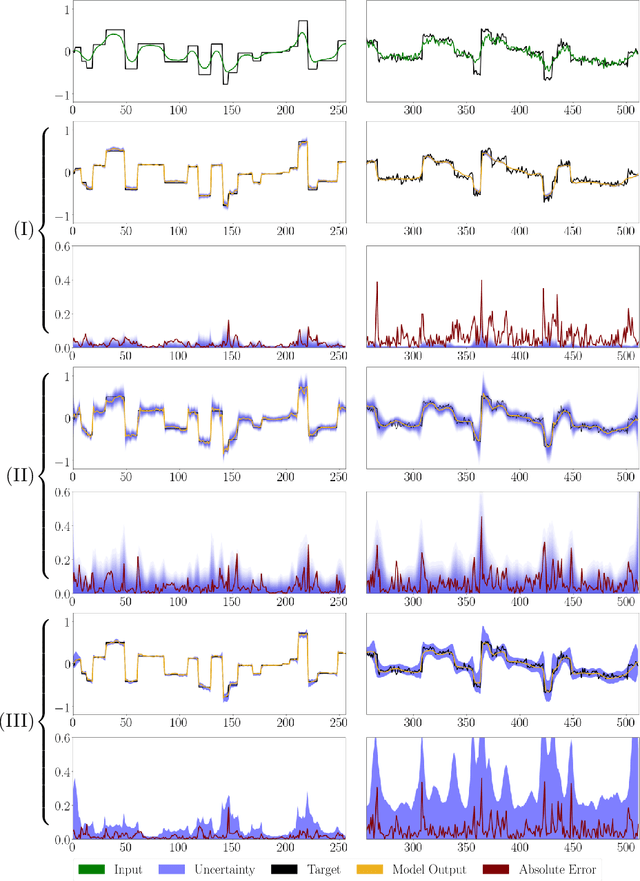
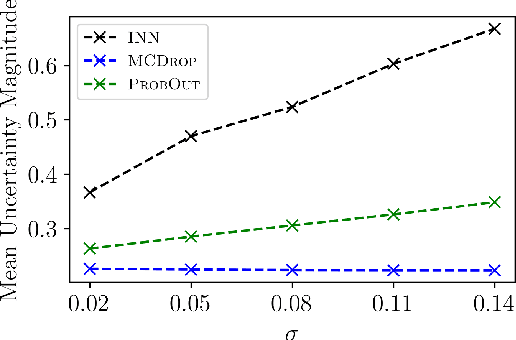
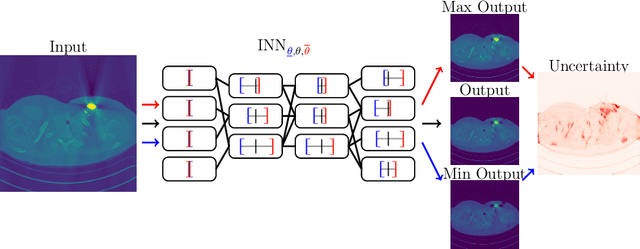
We propose a fast, non-Bayesian method for producing uncertainty scores in the output of pre-trained deep neural networks (DNNs) using a data-driven interval propagating network. This interval neural network (INN) has interval valued parameters and propagates its input using interval arithmetic. The INN produces sensible lower and upper bounds encompassing the ground truth. We provide theoretical justification for the validity of these bounds. Furthermore, its asymmetric uncertainty scores offer additional, directional information beyond what Gaussian-based, symmetric variance estimation can provide. We find that noise in the data is adequately captured by the intervals produced with our method. In numerical experiments on an image reconstruction task, we demonstrate the practical utility of INNs as a proxy for the prediction error in comparison to two state-of-the-art uncertainty quantification methods. In summary, INNs produce fast, theoretically justified uncertainty scores for DNNs that are easy to interpret, come with added information and pose as improved error proxies - features that may prove useful in advancing the usability of DNNs especially in sensitive applications such as health care.