Cosmas Heiß
Multi-level Neural Networks for high-dimensional parametric obstacle problems
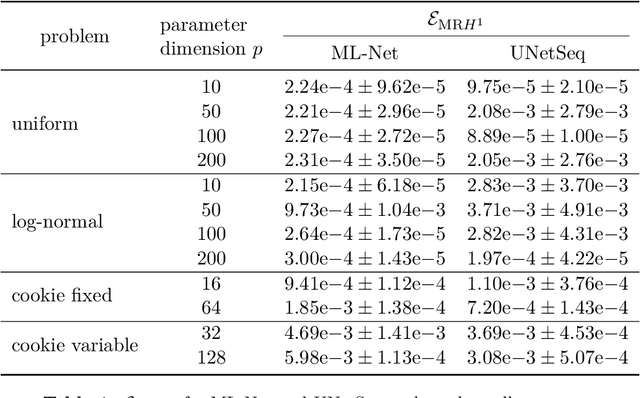
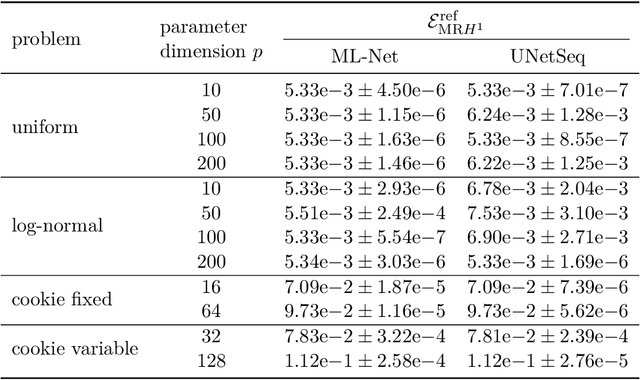
Apr 07, 2025Abstract:A new method to solve computationally challenging (random) parametric obstacle problems is developed and analyzed, where the parameters can influence the related partial differential equation (PDE) and determine the position and surface structure of the obstacle. As governing equation, a stationary elliptic diffusion problem is assumed. The high-dimensional solution of the obstacle problem is approximated by a specifically constructed convolutional neural network (CNN). This novel algorithm is inspired by a finite element constrained multigrid algorithm to represent the parameter to solution map. This has two benefits: First, it allows for efficient practical computations since multi-level data is used as an explicit output of the NN thanks to an appropriate data preprocessing. This improves the efficacy of the training process and subsequently leads to small errors in the natural energy norm. Second, the comparison of the CNN to a multigrid algorithm provides means to carry out a complete a priori convergence and complexity analysis of the proposed NN architecture. Numerical experiments illustrate a state-of-the-art performance for this challenging problem.
Multilevel CNNs for Parametric PDEs
Apr 04, 2023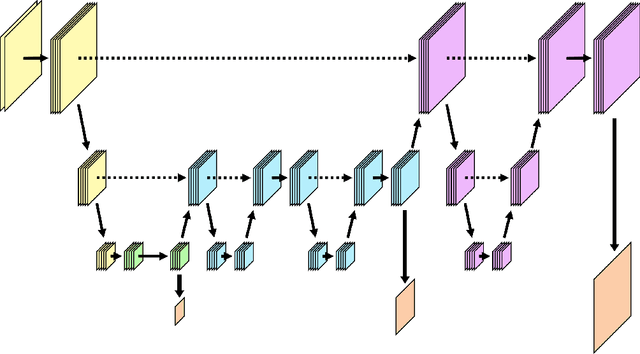

Abstract:We combine concepts from multilevel solvers for partial differential equations (PDEs) with neural network based deep learning and propose a new methodology for the efficient numerical solution of high-dimensional parametric PDEs. An in-depth theoretical analysis shows that the proposed architecture is able to approximate multigrid V-cycles to arbitrary precision with the number of weights only depending logarithmically on the resolution of the finest mesh. As a consequence, approximation bounds for the solution of parametric PDEs by neural networks that are independent on the (stochastic) parameter dimension can be derived. The performance of the proposed method is illustrated on high-dimensional parametric linear elliptic PDEs that are common benchmark problems in uncertainty quantification. We find substantial improvements over state-of-the-art deep learning-based solvers. As particularly challenging examples, random conductivity with high-dimensional non-affine Gaussian fields in 100 parameter dimensions and a random cookie problem are examined. Due to the multilevel structure of our method, the amount of training samples can be reduced on finer levels, hence significantly lowering the generation time for training data and the training time of our method.
Self-Supervised Equivariant Scene Synthesis from Video
Feb 01, 2021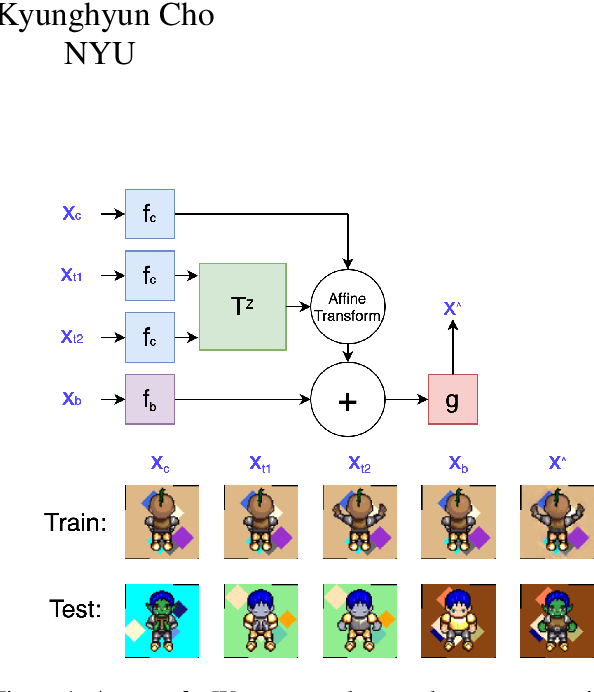
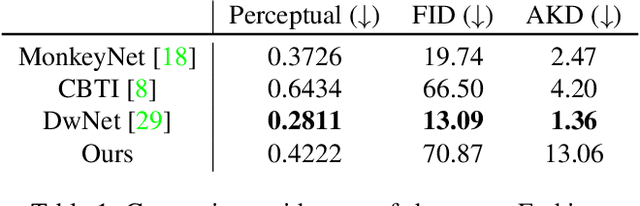
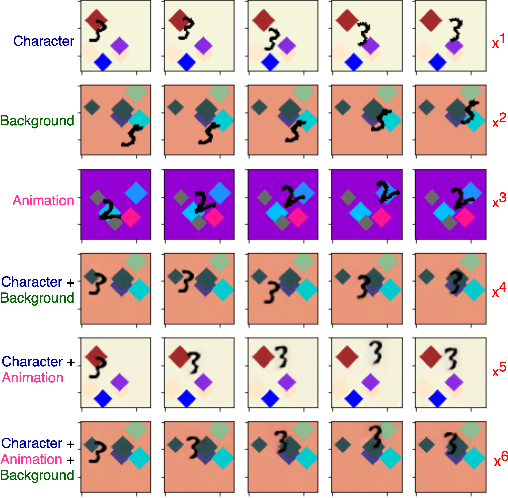
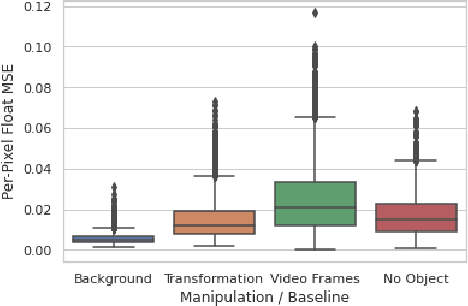
Abstract:We propose a self-supervised framework to learn scene representations from video that are automatically delineated into background, characters, and their animations. Our method capitalizes on moving characters being equivariant with respect to their transformation across frames and the background being constant with respect to that same transformation. After training, we can manipulate image encodings in real time to create unseen combinations of the delineated components. As far as we know, we are the first method to perform unsupervised extraction and synthesis of interpretable background, character, and animation. We demonstrate results on three datasets: Moving MNIST with backgrounds, 2D video game sprites, and Fashion Modeling.
In-Distribution Interpretability for Challenging Modalities
Jul 07, 2020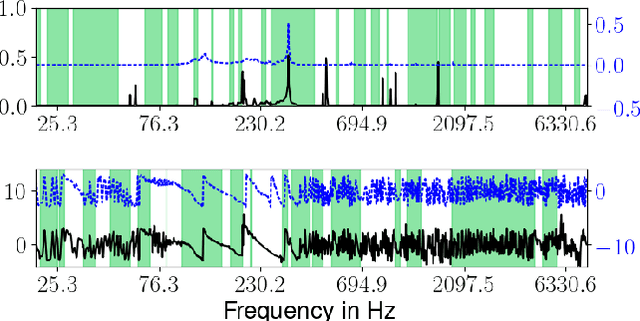
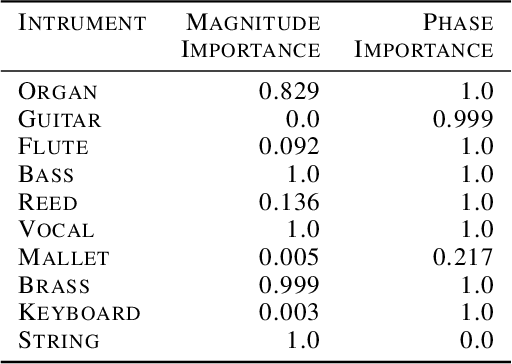
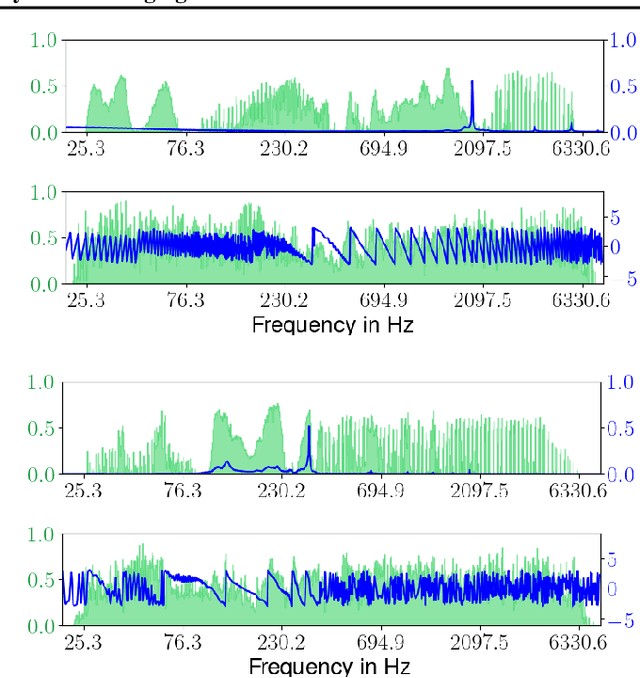
Abstract:It is widely recognized that the predictions of deep neural networks are difficult to parse relative to simpler approaches. However, the development of methods to investigate the mode of operation of such models has advanced rapidly in the past few years. Recent work introduced an intuitive framework which utilizes generative models to improve on the meaningfulness of such explanations. In this work, we display the flexibility of this method to interpret diverse and challenging modalities: music and physical simulations of urban environments.
Interval Neural Networks: Uncertainty Scores
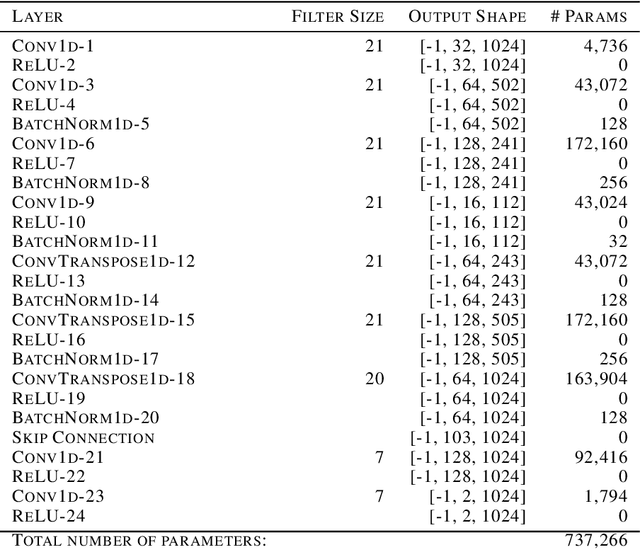
Mar 25, 2020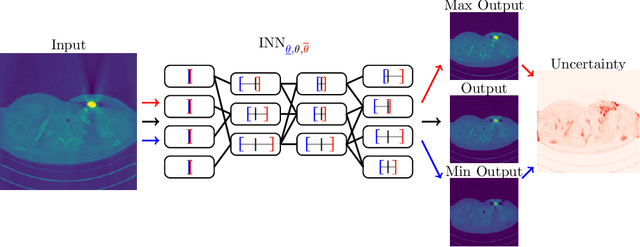
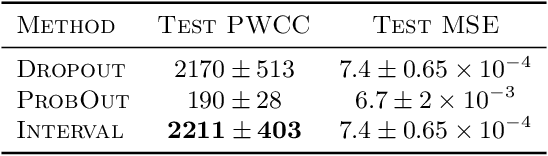
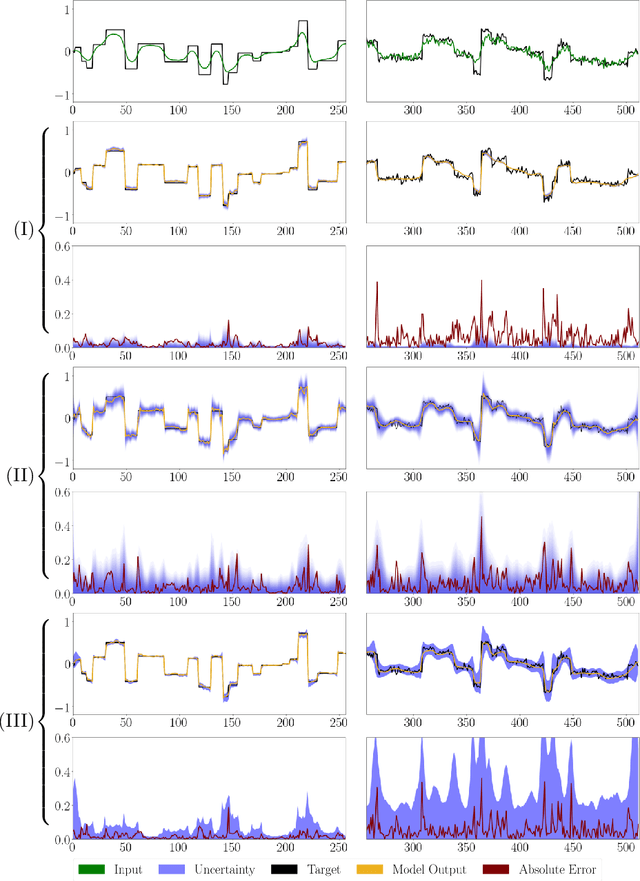
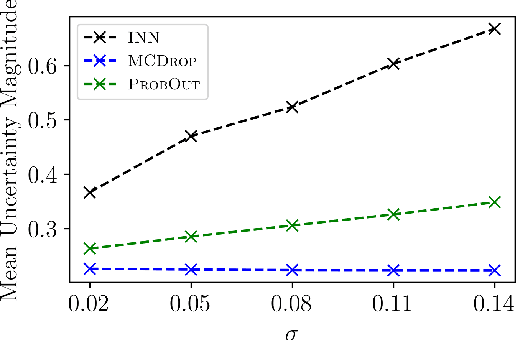
Abstract:We propose a fast, non-Bayesian method for producing uncertainty scores in the output of pre-trained deep neural networks (DNNs) using a data-driven interval propagating network. This interval neural network (INN) has interval valued parameters and propagates its input using interval arithmetic. The INN produces sensible lower and upper bounds encompassing the ground truth. We provide theoretical justification for the validity of these bounds. Furthermore, its asymmetric uncertainty scores offer additional, directional information beyond what Gaussian-based, symmetric variance estimation can provide. We find that noise in the data is adequately captured by the intervals produced with our method. In numerical experiments on an image reconstruction task, we demonstrate the practical utility of INNs as a proxy for the prediction error in comparison to two state-of-the-art uncertainty quantification methods. In summary, INNs produce fast, theoretically justified uncertainty scores for DNNs that are easy to interpret, come with added information and pose as improved error proxies - features that may prove useful in advancing the usability of DNNs especially in sensitive applications such as health care.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge