Multilevel CNNs for Parametric PDEs

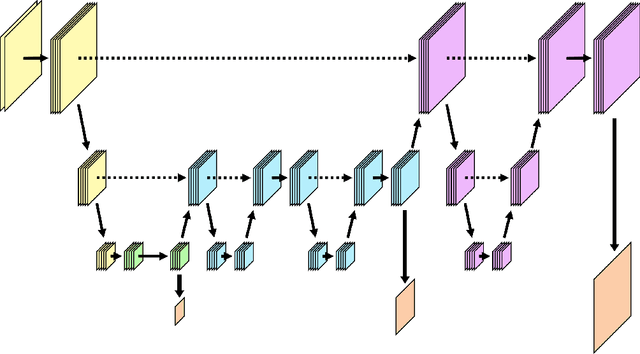
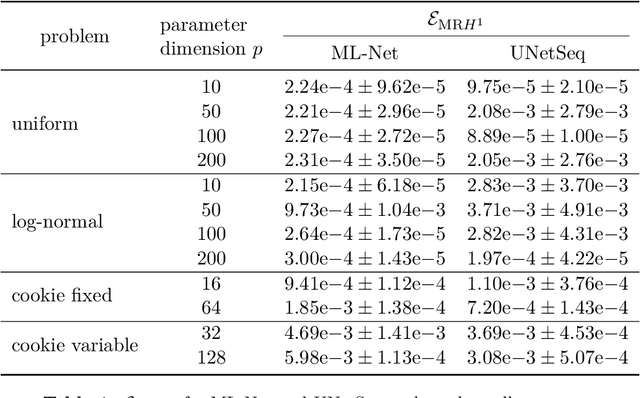
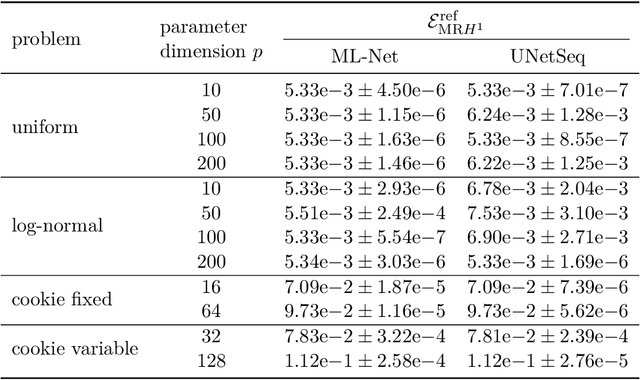
We combine concepts from multilevel solvers for partial differential equations (PDEs) with neural network based deep learning and propose a new methodology for the efficient numerical solution of high-dimensional parametric PDEs. An in-depth theoretical analysis shows that the proposed architecture is able to approximate multigrid V-cycles to arbitrary precision with the number of weights only depending logarithmically on the resolution of the finest mesh. As a consequence, approximation bounds for the solution of parametric PDEs by neural networks that are independent on the (stochastic) parameter dimension can be derived. The performance of the proposed method is illustrated on high-dimensional parametric linear elliptic PDEs that are common benchmark problems in uncertainty quantification. We find substantial improvements over state-of-the-art deep learning-based solvers. As particularly challenging examples, random conductivity with high-dimensional non-affine Gaussian fields in 100 parameter dimensions and a random cookie problem are examined. Due to the multilevel structure of our method, the amount of training samples can be reduced on finer levels, hence significantly lowering the generation time for training data and the training time of our method.

Near-Exact Recovery for Tomographic Inverse Problems via Deep Learning

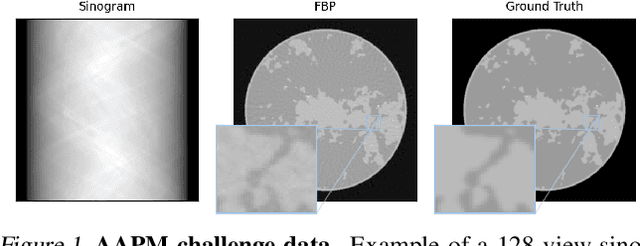
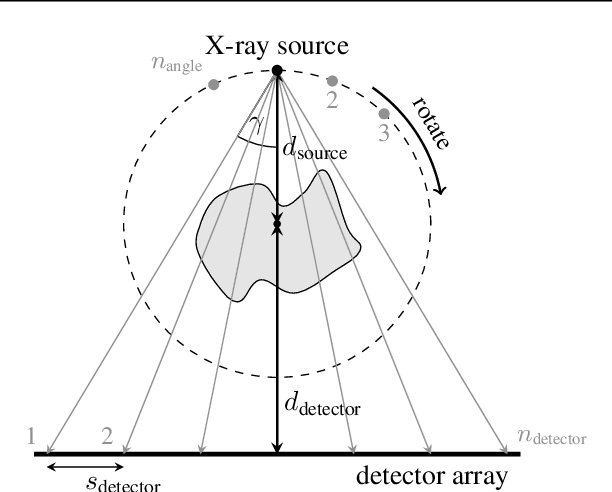
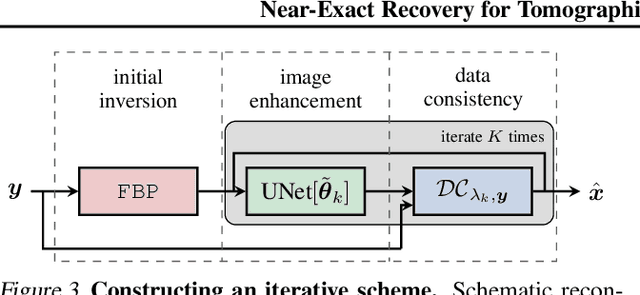
This work is concerned with the following fundamental question in scientific machine learning: Can deep-learning-based methods solve noise-free inverse problems to near-perfect accuracy? Positive evidence is provided for the first time, focusing on a prototypical computed tomography (CT) setup. We demonstrate that an iterative end-to-end network scheme enables reconstructions close to numerical precision, comparable to classical compressed sensing strategies. Our results build on our winning submission to the recent AAPM DL-Sparse-View CT Challenge. Its goal was to identify the state-of-the-art in solving the sparse-view CT inverse problem with data-driven techniques. A specific difficulty of the challenge setup was that the precise forward model remained unknown to the participants. Therefore, a key feature of our approach was to initially estimate the unknown fanbeam geometry in a data-driven calibration step. Apart from an in-depth analysis of our methodology, we also demonstrate its state-of-the-art performance on the open-access real-world dataset LoDoPaB CT.

Expressivity of Deep Neural Networks

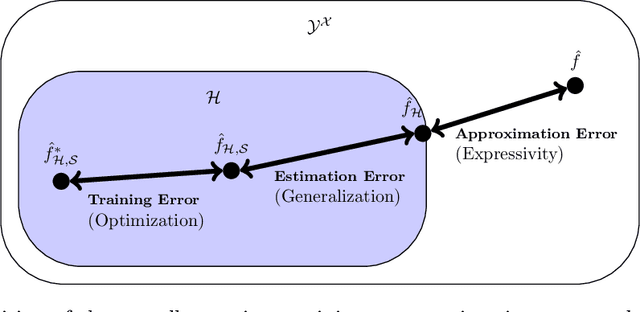
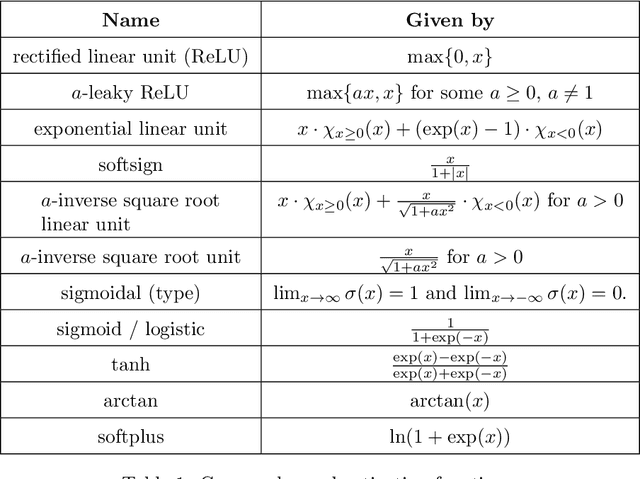
In this review paper, we give a comprehensive overview of the large variety of approximation results for neural networks. Approximation rates for classical function spaces as well as benefits of deep neural networks over shallow ones for specifically structured function classes are discussed. While the mainbody of existing results is for general feedforward architectures, we also depict approximation results for convolutional, residual and recurrent neural networks.

Error bounds for approximations with deep ReLU neural networks in $W^{s,p}$ norms

We analyze approximation rates of deep ReLU neural networks for Sobolev-regular functions with respect to weaker Sobolev norms. First, we construct, based on a calculus of ReLU networks, artificial neural networks with ReLU activation functions that achieve certain approximation rates. Second, we establish lower bounds for the approximation by ReLU neural networks for classes of Sobolev-regular functions. Our results extend recent advances in the approximation theory of ReLU networks to the regime that is most relevant for applications in the numerical analysis of partial differential equations.