Deep Learning based Forecasting: a case study from the online fashion industry

Demand forecasting in the online fashion industry is particularly amendable to global, data-driven forecasting models because of the industry's set of particular challenges. These include the volume of data, the irregularity, the high amount of turn-over in the catalog and the fixed inventory assumption. While standard deep learning forecasting approaches cater for many of these, the fixed inventory assumption requires a special treatment via controlling the relationship between price and demand closely. In this case study, we describe the data and our modelling approach for this forecasting problem in detail and present empirical results that highlight the effectiveness of our approach.

Expressivity of Deep Neural Networks

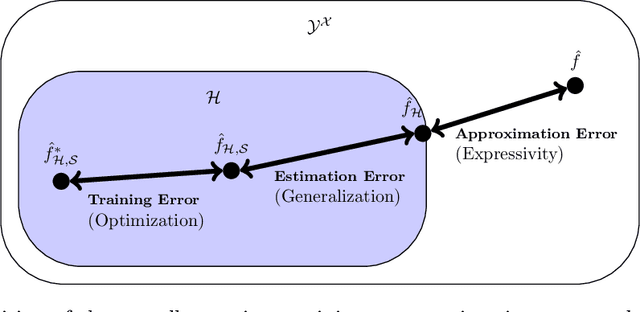
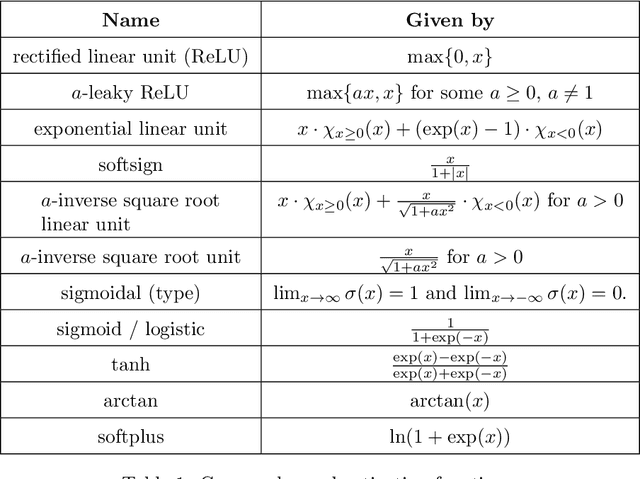
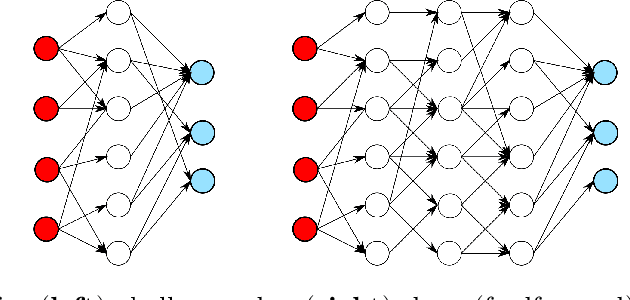
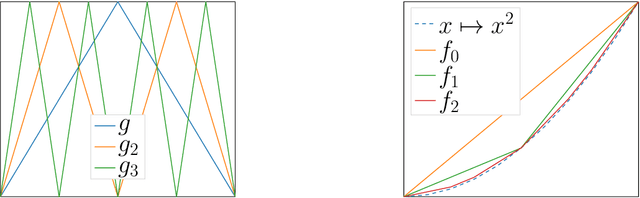
In this review paper, we give a comprehensive overview of the large variety of approximation results for neural networks. Approximation rates for classical function spaces as well as benefits of deep neural networks over shallow ones for specifically structured function classes are discussed. While the mainbody of existing results is for general feedforward architectures, we also depict approximation results for convolutional, residual and recurrent neural networks.

Numerical Solution of the Parametric Diffusion Equation by Deep Neural Networks

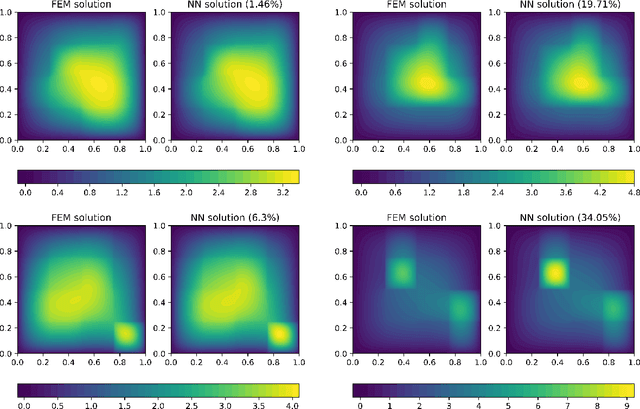
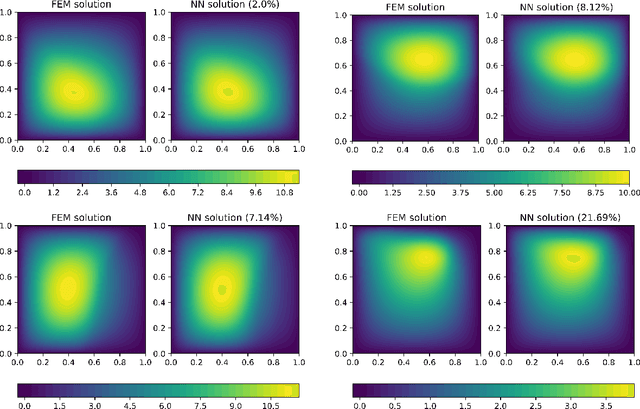
We perform a comprehensive numerical study of the effect of approximation-theoretical results for neural networks on practical learning problems in the context of numerical analysis. As the underlying model, we study the machine-learning-based solution of parametric partial differential equations. Here, approximation theory predicts that the performance of the model should depend only very mildly on the dimension of the parameter space and is determined by the intrinsic dimension of the solution manifold of the parametric partial differential equation. We use various methods to establish comparability between test-cases by minimizing the effect of the choice of test-cases on the optimization and sampling aspects of the learning problem. We find strong support for the hypothesis that approximation-theoretical effects heavily influence the practical behavior of learning problems in numerical analysis.

A Theoretical Analysis of Deep Neural Networks and Parametric PDEs

We derive upper bounds on the complexity of ReLU neural networks approximating the solution maps of parametric partial differential equations. In particular, without any knowledge of its concrete shape, we use the inherent low-dimensionality of the solution manifold to obtain approximation rates which are significantly superior to those provided by classical approximation results. We use this low dimensionality to guarantee the existence of a reduced basis. Then, for a large variety of parametric partial differential equations, we construct neural networks that yield approximations of the parametric maps not suffering from a curse of dimension and essentially only depending on the size of the reduced basis.