A block-sparse Tensor Train Format for sample-efficient high-dimensional Polynomial Regression

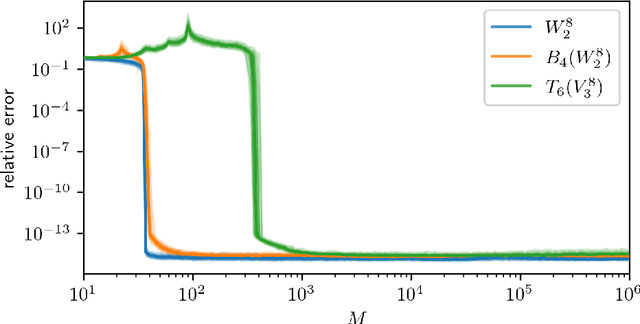
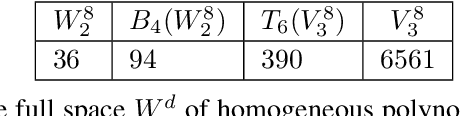
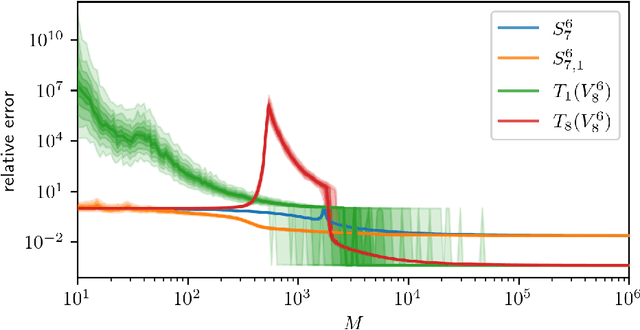
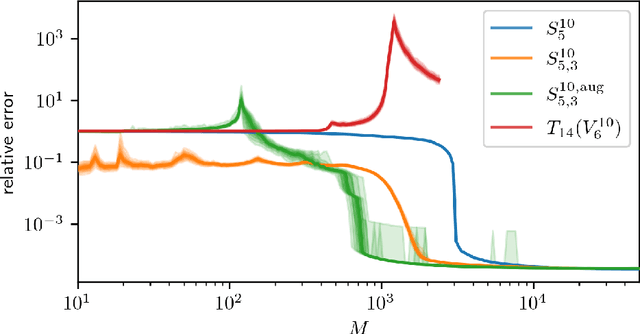
Low-rank tensors are an established framework for high-dimensional least-squares problems. We propose to extend this framework by including the concept of block-sparsity. In the context of polynomial regression each sparsity pattern corresponds to some subspace of homogeneous multivariate polynomials. This allows us to adapt the ansatz space to align better with known sample complexity results. The resulting method is tested in numerical experiments and demonstrates improved computational resource utilization and sample efficiency.

Numerical Solution of the Parametric Diffusion Equation by Deep Neural Networks

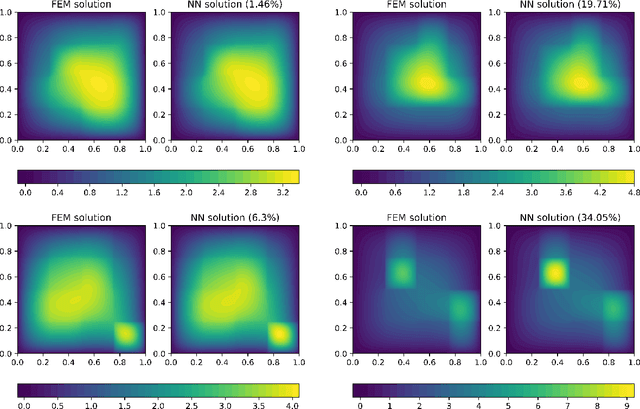
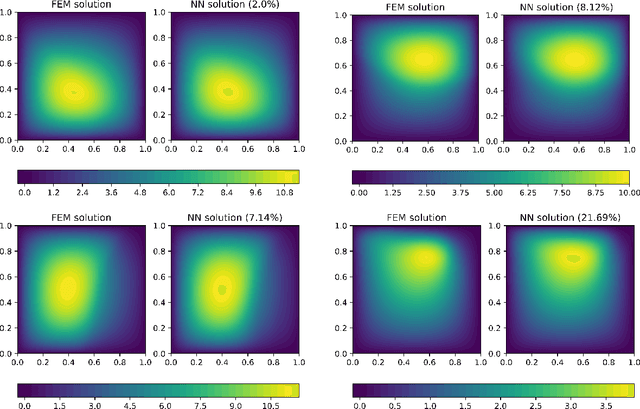
We perform a comprehensive numerical study of the effect of approximation-theoretical results for neural networks on practical learning problems in the context of numerical analysis. As the underlying model, we study the machine-learning-based solution of parametric partial differential equations. Here, approximation theory predicts that the performance of the model should depend only very mildly on the dimension of the parameter space and is determined by the intrinsic dimension of the solution manifold of the parametric partial differential equation. We use various methods to establish comparability between test-cases by minimizing the effect of the choice of test-cases on the optimization and sampling aspects of the learning problem. We find strong support for the hypothesis that approximation-theoretical effects heavily influence the practical behavior of learning problems in numerical analysis.

A Theoretical Analysis of Deep Neural Networks and Parametric PDEs

We derive upper bounds on the complexity of ReLU neural networks approximating the solution maps of parametric partial differential equations. In particular, without any knowledge of its concrete shape, we use the inherent low-dimensionality of the solution manifold to obtain approximation rates which are significantly superior to those provided by classical approximation results. We use this low dimensionality to guarantee the existence of a reduced basis. Then, for a large variety of parametric partial differential equations, we construct neural networks that yield approximations of the parametric maps not suffering from a curse of dimension and essentially only depending on the size of the reduced basis.

Convergence results for projected line-search methods on varieties of low-rank matrices via Łojasiewicz inequality

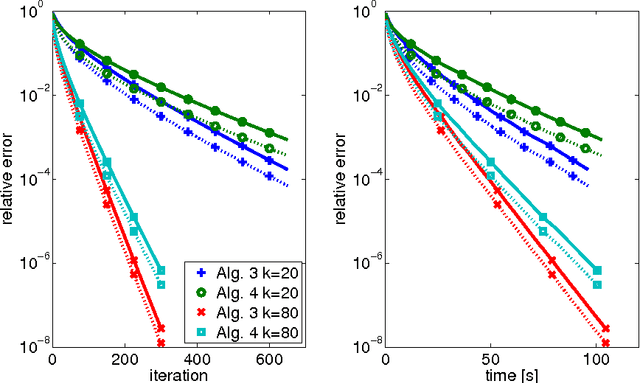
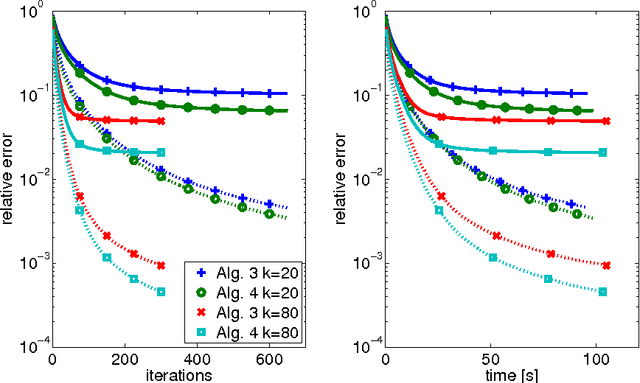
The aim of this paper is to derive convergence results for projected line-search methods on the real-algebraic variety $\mathcal{M}_{\le k}$ of real $m \times n$ matrices of rank at most $k$. Such methods extend Riemannian optimization methods, which are successfully used on the smooth manifold $\mathcal{M}_k$ of rank-$k$ matrices, to its closure by taking steps along gradient-related directions in the tangent cone, and afterwards projecting back to $\mathcal{M}_{\le k}$. Considering such a method circumvents the difficulties which arise from the nonclosedness and the unbounded curvature of $\mathcal{M}_k$. The pointwise convergence is obtained for real-analytic functions on the basis of a \L{}ojasiewicz inequality for the projection of the antigradient to the tangent cone. If the derived limit point lies on the smooth part of $\mathcal{M}_{\le k}$, i.e. in $\mathcal{M}_k$, this boils down to more or less known results, but with the benefit that asymptotic convergence rate estimates (for specific step-sizes) can be obtained without an a priori curvature bound, simply from the fact that the limit lies on a smooth manifold. At the same time, one can give a convincing justification for assuming critical points to lie in $\mathcal{M}_k$: if $X$ is a critical point of $f$ on $\mathcal{M}_{\le k}$, then either $X$ has rank $k$, or $\nabla f(X) = 0$.