High-dimensional classification problems with Barron regular boundaries under margin conditions

We prove that a classifier with a Barron-regular decision boundary can be approximated with a rate of high polynomial degree by ReLU neural networks with three hidden layers when a margin condition is assumed. In particular, for strong margin conditions, high-dimensional discontinuous classifiers can be approximated with a rate that is typically only achievable when approximating a low-dimensional smooth function. We demonstrate how these expression rate bounds imply fast-rate learning bounds that are close to $n^{-1}$ where $n$ is the number of samples. In addition, we carry out comprehensive numerical experimentation on binary classification problems with various margins. We study three different dimensions, with the highest dimensional problem corresponding to images from the MNIST data set.

The sampling complexity of learning invertible residual neural networks

In recent work it has been shown that determining a feedforward ReLU neural network to within high uniform accuracy from point samples suffers from the curse of dimensionality in terms of the number of samples needed. As a consequence, feedforward ReLU neural networks are of limited use for applications where guaranteed high uniform accuracy is required. We consider the question of whether the sampling complexity can be improved by restricting the specific neural network architecture. To this end, we investigate invertible residual neural networks which are foundational architectures in deep learning and are widely employed in models that power modern generative methods. Our main result shows that the residual neural network architecture and invertibility do not help overcome the complexity barriers encountered with simpler feedforward architectures. Specifically, we demonstrate that the computational complexity of approximating invertible residual neural networks from point samples in the uniform norm suffers from the curse of dimensionality. Similar results are established for invertible convolutional Residual neural networks.

Dimension-independent learning rates for high-dimensional classification problems

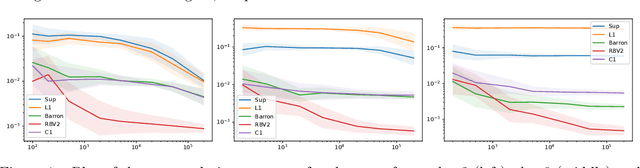
We study the problem of approximating and estimating classification functions that have their decision boundary in the $RBV^2$ space. Functions of $RBV^2$ type arise naturally as solutions of regularized neural network learning problems and neural networks can approximate these functions without the curse of dimensionality. We modify existing results to show that every $RBV^2$ function can be approximated by a neural network with bounded weights. Thereafter, we prove the existence of a neural network with bounded weights approximating a classification function. And we leverage these bounds to quantify the estimation rates. Finally, we present a numerical study that analyzes the effect of different regularity conditions on the decision boundaries.

Mathematical theory of deep learning

This book provides an introduction to the mathematical analysis of deep learning. It covers fundamental results in approximation theory, optimization theory, and statistical learning theory, which are the three main pillars of deep neural network theory. Serving as a guide for students and researchers in mathematics and related fields, the book aims to equip readers with foundational knowledge on the topic. It prioritizes simplicity over generality, and presents rigorous yet accessible results to help build an understanding of the essential mathematical concepts underpinning deep learning.

Large Language Models for Mathematicians

Large language models (LLMs) such as ChatGPT have received immense interest for their general-purpose language understanding and, in particular, their ability to generate high-quality text or computer code. For many professions, LLMs represent an invaluable tool that can speed up and improve the quality of work. In this note, we discuss to what extent they can aid professional mathematicians. We first provide a mathematical description of the transformer model used in all modern language models. Based on recent studies, we then outline best practices and potential issues and report on the mathematical abilities of language models. Finally, we shed light on the potential of LMMs to change how mathematicians work.

Optimal learning of high-dimensional classification problems using deep neural networks

We study the problem of learning classification functions from noiseless training samples, under the assumption that the decision boundary is of a certain regularity. We establish universal lower bounds for this estimation problem, for general classes of continuous decision boundaries. For the class of locally Barron-regular decision boundaries, we find that the optimal estimation rates are essentially independent of the underlying dimension and can be realized by empirical risk minimization methods over a suitable class of deep neural networks. These results are based on novel estimates of the $L^1$ and $L^\infty$ entropies of the class of Barron-regular functions.

Deep Microlocal Reconstruction for Limited-Angle Tomography

We present a deep learning-based algorithm to jointly solve a reconstruction problem and a wavefront set extraction problem in tomographic imaging. The algorithm is based on a recently developed digital wavefront set extractor as well as the well-known microlocal canonical relation for the Radon transform. We use the wavefront set information about x-ray data to improve the reconstruction by requiring that the underlying neural networks simultaneously extract the correct ground truth wavefront set and ground truth image. As a necessary theoretical step, we identify the digital microlocal canonical relations for deep convolutional residual neural networks. We find strong numerical evidence for the effectiveness of this approach.

The Modern Mathematics of Deep Learning

We describe the new field of mathematical analysis of deep learning. This field emerged around a list of research questions that were not answered within the classical framework of learning theory. These questions concern: the outstanding generalization power of overparametrized neural networks, the role of depth in deep architectures, the apparent absence of the curse of dimensionality, the surprisingly successful optimization performance despite the non-convexity of the problem, understanding what features are learned, why deep architectures perform exceptionally well in physical problems, and which fine aspects of an architecture affect the behavior of a learning task in which way. We present an overview of modern approaches that yield partial answers to these questions. For selected approaches, we describe the main ideas in more detail.

Neural network approximation and estimation of classifiers with classification boundary in a Barron class

We prove bounds for the approximation and estimation of certain classification functions using ReLU neural networks. Our estimation bounds provide a priori performance guarantees for empirical risk minimization using networks of a suitable size, depending on the number of training samples available. The obtained approximation and estimation rates are independent of the dimension of the input, showing that the curse of dimension can be overcome in this setting; in fact, the input dimension only enters in the form of a polynomial factor. Regarding the regularity of the target classification function, we assume the interfaces between the different classes to be locally of Barron-type. We complement our results by studying the relations between various Barron-type spaces that have been proposed in the literature. These spaces differ substantially more from each other than the current literature suggests.

Numerical Solution of the Parametric Diffusion Equation by Deep Neural Networks

We perform a comprehensive numerical study of the effect of approximation-theoretical results for neural networks on practical learning problems in the context of numerical analysis. As the underlying model, we study the machine-learning-based solution of parametric partial differential equations. Here, approximation theory predicts that the performance of the model should depend only very mildly on the dimension of the parameter space and is determined by the intrinsic dimension of the solution manifold of the parametric partial differential equation. We use various methods to establish comparability between test-cases by minimizing the effect of the choice of test-cases on the optimization and sampling aspects of the learning problem. We find strong support for the hypothesis that approximation-theoretical effects heavily influence the practical behavior of learning problems in numerical analysis.