Dispelling the Curse of Singularities in Neural Network Optimizations

This work investigates the optimization instability of deep neural networks from a less-explored yet insightful perspective: the emergence and amplification of singularities in the parametric space. Our analysis reveals that parametric singularities inevitably grow with gradient updates and further intensify alignment with representations, leading to increased singularities in the representation space. We show that the gradient Frobenius norms are bounded by the top singular values of the weight matrices, and as training progresses, the mutually reinforcing growth of weight and representation singularities, termed the curse of singularities, relaxes these bounds, escalating the risk of sharp loss explosions. To counter this, we propose Parametric Singularity Smoothing (PSS), a lightweight, flexible, and effective method for smoothing the singular spectra of weight matrices. Extensive experiments across diverse datasets, architectures, and optimizers demonstrate that PSS mitigates instability, restores trainability even after failure, and improves both training efficiency and generalization.

On the Spectral Flattening of Quantized Embeddings

Training Large Language Models (LLMs) at ultra-low precision is critically impeded by instability rooted in the conflict between discrete quantization constraints and the intrinsic heavy-tailed spectral nature of linguistic data. By formalizing the connection between Zipfian statistics and random matrix theory, we prove that the power-law decay in the singular value spectra of embeddings is a fundamental requisite for semantic encoding. We derive theoretical bounds showing that uniform quantization introduces a noise floor that disproportionately truncates this spectral tail, which induces spectral flattening and a strictly provable increase in the stable rank of representations. Empirical validation across diverse architectures including GPT-2 and TinyLlama corroborates that this geometric degradation precipitates representational collapse. This work not only quantifies the spectral sensitivity of LLMs but also establishes spectral fidelity as a necessary condition for stable low-bit optimization.

LAMP: Look-Ahead Mixed-Precision Inference of Large Language Models

Mixed-precision computations are a hallmark of the current stage of AI, driving the progress in large language models towards efficient, locally deployable solutions. This article addresses the floating-point computation of compositionally-rich functions, concentrating on transformer inference. Based on the rounding error analysis of a composition $f(g(\mathrm{x}))$, we provide an adaptive strategy that selects a small subset of components of $g(\mathrm{x})$ to be computed more accurately while all other computations can be carried out with lower accuracy. We then explain how this strategy can be applied to different compositions within a transformer and illustrate its overall effect on transformer inference. We study the effectiveness of this algorithm numerically on GPT-2 models and demonstrate that already very low recomputation rates allow for improvements of up to two orders of magnitude in accuracy.

Transferable text data distillation by trajectory matching

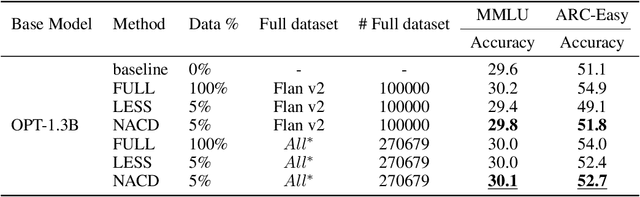
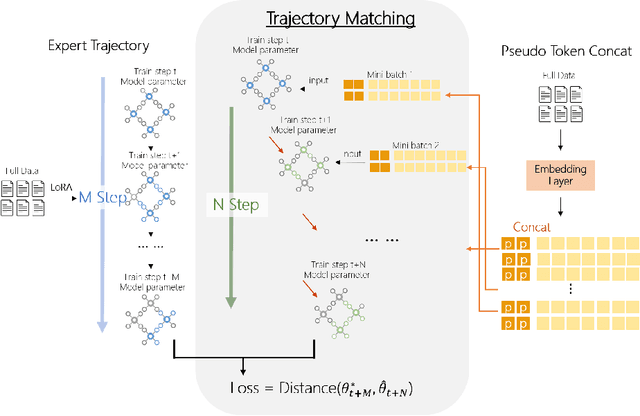
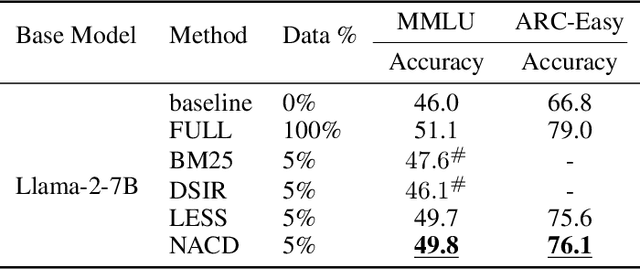
In the realm of large language model (LLM), as the size of large models increases, it also brings higher training costs. There is a urgent need to minimize the data size in LLM training. Compared with data selection method, the data distillation method aims to synthesize a small number of data samples to achieve the training effect of the full data set and has better flexibility. Despite its successes in computer vision, the discreteness of text data has hitherto stymied its exploration in natural language processing (NLP). In this work, we proposed a method that involves learning pseudo prompt data based on trajectory matching and finding its nearest neighbor ID to achieve cross-architecture transfer. During the distillation process, we introduce a regularization loss to improve the robustness of our distilled data. To our best knowledge, this is the first data distillation work suitable for text generation tasks such as instruction tuning. Evaluations on two benchmarks, including ARC-Easy and MMLU instruction tuning datasets, established the superiority of our distillation approach over the SOTA data selection method LESS. Furthermore, our method demonstrates a good transferability over LLM structures (i.e., OPT to Llama).

Numerical Error Analysis of Large Language Models

Large language models based on transformer architectures have become integral to state-of-the-art natural language processing applications. However, their training remains computationally expensive and exhibits instabilities, some of which are expected to be caused by finite-precision computations. We provide a theoretical analysis of the impact of round-off errors within the forward pass of a transformer architecture which yields fundamental bounds for these effects. In addition, we conduct a series of numerical experiments which demonstrate the practical relevance of our bounds. Our results yield concrete guidelines for choosing hyperparameters that mitigate round-off errors, leading to more robust and stable inference.

PLPP: Prompt Learning with Perplexity Is Self-Distillation for Vision-Language Models

Pre-trained Vision-Language (VL) models such as CLIP have demonstrated their excellent performance across numerous downstream tasks. A recent method, Context Optimization (CoOp), further improves the performance of VL models on downstream tasks by introducing prompt learning. CoOp optimizes a set of learnable vectors, aka prompt, and freezes the whole CLIP model. However, relying solely on CLIP loss to fine-tune prompts can lead to models that are prone to overfitting on downstream task. To address this issue, we propose a plug-in prompt-regularization method called PLPP (Prompt Learning with PerPlexity), which use perplexity loss to regularize prompt learning. PLPP designs a two-step operation to compute the perplexity for prompts: (a) calculating cosine similarity between the weight of the embedding layer and prompts to get labels, (b) introducing a language model (LM) head that requires no training behind text encoder to output word probability distribution. Meanwhile, we unveil that the essence of PLPP is inherently a form of self-distillation. To further prevent overfitting as well as to reduce the additional computation introduced by PLPP, we turn the hard label to soft label and choose top-$k$ values for calculating the perplexity loss. For accelerating model convergence, we introduce mutual self-distillation learning, that is perplexity and inverted perplexity loss. The experiments conducted on four classification tasks indicate that PLPP exhibits superior performance compared to existing methods.

Training Overhead Ratio: A Practical Reliability Metric for Large Language Model Training Systems

Large Language Models (LLMs) are revolutionizing the AI industry with their superior capabilities. Training these models requires large-scale GPU clusters and significant computing time, leading to frequent failures that significantly increase training costs. Despite its significance, this field lacks a metric for evaluating reliability. In this work, we introduce a novel reliability metric called \emph{Training Overhead Ratio} (TOR) to evaluate the reliability of fault-tolerant LLM training systems. TOR is defined as the ratio of optimal training time to the observed training time of a system, serving as a practical tool for users to estimate the actual time required to train an LLM on a given system. Furthermore, our investigation identifies the key factor for enhancing reliability and present TOR equations for various types of failures encountered in practice.