Adaptive Kernel Selection for Stein Variational Gradient Descent

A central challenge in Bayesian inference is efficiently approximating posterior distributions. Stein Variational Gradient Descent (SVGD) is a popular variational inference method which transports a set of particles to approximate a target distribution. The SVGD dynamics are governed by a reproducing kernel Hilbert space (RKHS) and are highly sensitive to the choice of the kernel function, which directly influences both convergence and approximation quality. The commonly used median heuristic offers a simple approach for setting kernel bandwidths but lacks flexibility and often performs poorly, particularly in high-dimensional settings. In this work, we propose an alternative strategy for adaptively choosing kernel parameters over an abstract family of kernels. Recent convergence analyses based on the kernelized Stein discrepancy (KSD) suggest that optimizing the kernel parameters by maximizing the KSD can improve performance. Building on this insight, we introduce Adaptive SVGD (Ad-SVGD), a method that alternates between updating the particles via SVGD and adaptively tuning kernel bandwidths through gradient ascent on the KSD. We provide a simplified theoretical analysis that extends existing results on minimizing the KSD for fixed kernels to our adaptive setting, showing convergence properties for the maximal KSD over our kernel class. Our empirical results further support this intuition: Ad-SVGD consistently outperforms standard heuristics in a variety of tasks.

Optimal Scheduling of Dynamic Transport

Flow-based methods for sampling and generative modeling use continuous-time dynamical systems to represent a {transport map} that pushes forward a source measure to a target measure. The introduction of a time axis provides considerable design freedom, and a central question is how to exploit this freedom. Though many popular methods seek straight line (i.e., zero acceleration) trajectories, we show here that a specific class of ``curved'' trajectories can significantly improve approximation and learning. In particular, we consider the unit-time interpolation of any given transport map $T$ and seek the schedule $\tau: [0,1] \to [0,1]$ that minimizes the spatial Lipschitz constant of the corresponding velocity field over all times $t \in [0,1]$. This quantity is crucial as it allows for control of the approximation error when the velocity field is learned from data. We show that, for a broad class of source/target measures and transport maps $T$, the \emph{optimal schedule} can be computed in closed form, and that the resulting optimal Lipschitz constant is \emph{exponentially smaller} than that induced by an identity schedule (corresponding to, for instance, the Wasserstein geodesic). Our proof technique relies on the calculus of variations and $\Gamma$-convergence, allowing us to approximate the aforementioned degenerate objective by a family of smooth, tractable problems.

Low Stein Discrepancy via Message-Passing Monte Carlo

Message-Passing Monte Carlo (MPMC) was recently introduced as a novel low-discrepancy sampling approach leveraging tools from geometric deep learning. While originally designed for generating uniform point sets, we extend this framework to sample from general multivariate probability distributions with known probability density function. Our proposed method, Stein-Message-Passing Monte Carlo (Stein-MPMC), minimizes a kernelized Stein discrepancy, ensuring improved sample quality. Finally, we show that Stein-MPMC outperforms competing methods, such as Stein Variational Gradient Descent and (greedy) Stein Points, by achieving a lower Stein discrepancy.

Mathematical theory of deep learning

This book provides an introduction to the mathematical analysis of deep learning. It covers fundamental results in approximation theory, optimization theory, and statistical learning theory, which are the three main pillars of deep neural network theory. Serving as a guide for students and researchers in mathematics and related fields, the book aims to equip readers with foundational knowledge on the topic. It prioritizes simplicity over generality, and presents rigorous yet accessible results to help build an understanding of the essential mathematical concepts underpinning deep learning.

Distribution learning via neural differential equations: a nonparametric statistical perspective

Ordinary differential equations (ODEs), via their induced flow maps, provide a powerful framework to parameterize invertible transformations for the purpose of representing complex probability distributions. While such models have achieved enormous success in machine learning, particularly for generative modeling and density estimation, little is known about their statistical properties. This work establishes the first general nonparametric statistical convergence analysis for distribution learning via ODE models trained through likelihood maximization. We first prove a convergence theorem applicable to arbitrary velocity field classes $\mathcal{F}$ satisfying certain simple boundary constraints. This general result captures the trade-off between approximation error (`bias') and the complexity of the ODE model (`variance'). We show that the latter can be quantified via the $C^1$-metric entropy of the class $\mathcal F$. We then apply this general framework to the setting of $C^k$-smooth target densities, and establish nearly minimax-optimal convergence rates for two relevant velocity field classes $\mathcal F$: $C^k$ functions and neural networks. The latter is the practically important case of neural ODEs. Our proof techniques require a careful synthesis of (i) analytical stability results for ODEs, (ii) classical theory for sieved M-estimators, and (iii) recent results on approximation rates and metric entropies of neural network classes. The results also provide theoretical insight on how the choice of velocity field class, and the dependence of this choice on sample size $n$ (e.g., the scaling of width, depth, and sparsity of neural network classes), impacts statistical performance.

Deep Operator Network Approximation Rates for Lipschitz Operators

We establish universality and expression rate bounds for a class of neural Deep Operator Networks (DON) emulating Lipschitz (or H\"older) continuous maps $\mathcal G:\mathcal X\to\mathcal Y$ between (subsets of) separable Hilbert spaces $\mathcal X$, $\mathcal Y$. The DON architecture considered uses linear encoders $\mathcal E$ and decoders $\mathcal D$ via (biorthogonal) Riesz bases of $\mathcal X$, $\mathcal Y$, and an approximator network of an infinite-dimensional, parametric coordinate map that is Lipschitz continuous on the sequence space $\ell^2(\mathbb N)$. Unlike previous works ([Herrmann, Schwab and Zech: Neural and Spectral operator surrogates: construction and expression rate bounds, SAM Report, 2022], [Marcati and Schwab: Exponential Convergence of Deep Operator Networks for Elliptic Partial Differential Equations, SAM Report, 2022]), which required for example $\mathcal G$ to be holomorphic, the present expression rate results require mere Lipschitz (or H\"older) continuity of $\mathcal G$. Key in the proof of the present expression rate bounds is the use of either super-expressive activations (e.g. [Yarotski: Elementary superexpressive activations, Int. Conf. on ML, 2021], [Shen, Yang and Zhang: Neural network approximation: Three hidden layers are enough, Neural Networks, 2021], and the references there) which are inspired by the Kolmogorov superposition theorem, or of nonstandard NN architectures with standard (ReLU) activations as recently proposed in [Zhang, Shen and Yang: Neural Network Architecture Beyond Width and Depth, Adv. in Neural Inf. Proc. Sys., 2022]. We illustrate the abstract results by approximation rate bounds for emulation of a) solution operators for parametric elliptic variational inequalities, and b) Lipschitz maps of Hilbert-Schmidt operators.

Neural and gpc operator surrogates: construction and expression rate bounds

Approximation rates are analyzed for deep surrogates of maps between infinite-dimensional function spaces, arising e.g. as data-to-solution maps of linear and nonlinear partial differential equations. Specifically, we study approximation rates for Deep Neural Operator and Generalized Polynomial Chaos (gpc) Operator surrogates for nonlinear, holomorphic maps between infinite-dimensional, separable Hilbert spaces. Operator in- and outputs from function spaces are assumed to be parametrized by stable, affine representation systems. Admissible representation systems comprise orthonormal bases, Riesz bases or suitable tight frames of the spaces under consideration. Algebraic expression rate bounds are established for both, deep neural and gpc operator surrogates acting in scales of separable Hilbert spaces containing domain and range of the map to be expressed, with finite Sobolev or Besov regularity. We illustrate the abstract concepts by expression rate bounds for the coefficient-to-solution map for a linear elliptic PDE on the torus.

De Rham compatible Deep Neural Networks

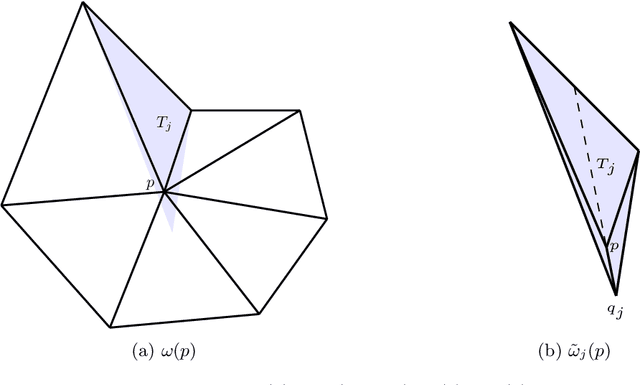
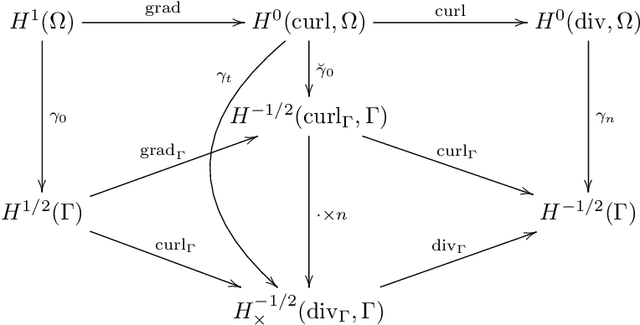
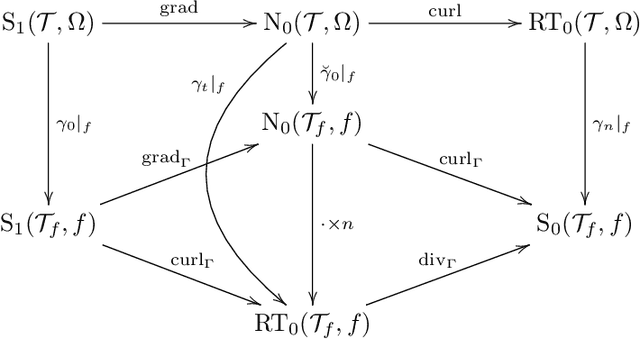
We construct several classes of neural networks with ReLU and BiSU (Binary Step Unit) activations, which exactly emulate the lowest order Finite Element (FE) spaces on regular, simplicial partitions of polygonal and polyhedral domains $\Omega \subset \mathbb{R}^d$, $d=2,3$. For continuous, piecewise linear (CPwL) functions, our constructions generalize previous results in that arbitrary, regular simplicial partitions of $\Omega$ are admitted, also in arbitrary dimension $d\geq 2$. Vector-valued elements emulated include the classical Raviart-Thomas and the first family of N\'{e}d\'{e}lec edge elements on triangles and tetrahedra. Neural Networks emulating these FE spaces are required in the correct approximation of boundary value problems of electromagnetism in nonconvex polyhedra $\Omega \subset \mathbb{R}^3$, thereby constituting an essential ingredient in the application of e.g. the methodology of ``physics-informed NNs'' or ``deep Ritz methods'' to electromagnetic field simulation via deep learning techniques. They satisfy exact (De Rham) sequence properties, and also spawn discrete boundary complexes on $\partial\Omega$ which satisfy exact sequence properties for the surface divergence and curl operators $\mathrm{div}_\Gamma$ and $\mathrm{curl}_\Gamma$, respectively, thereby enabling ``neural boundary elements'' for computational electromagnetism. We indicate generalizations of our constructions to higher-order compatible spaces and other, non-compatible classes of discretizations in particular the Crouzeix-Raviart elements and Hybridized, Higher Order (HHO) methods.

Deep Learning in High Dimension: Neural Network Approximation of Analytic Functions in $L^2(\mathbb{R}^d,γ_d)$

For artificial deep neural networks, we prove expression rates for analytic functions $f:\mathbb{R}^d\to\mathbb{R}$ in the norm of $L^2(\mathbb{R}^d,\gamma_d)$ where $d\in {\mathbb{N}}\cup\{ \infty \}$. Here $\gamma_d$ denotes the Gaussian product probability measure on $\mathbb{R}^d$. We consider in particular ReLU and ReLU${}^k$ activations for integer $k\geq 2$. For $d\in\mathbb{N}$, we show exponential convergence rates in $L^2(\mathbb{R}^d,\gamma_d)$. In case $d=\infty$, under suitable smoothness and sparsity assumptions on $f:\mathbb{R}^{\mathbb{N}}\to\mathbb{R}$, with $\gamma_\infty$ denoting an infinite (Gaussian) product measure on $\mathbb{R}^{\mathbb{N}}$, we prove dimension-independent expression rate bounds in the norm of $L^2(\mathbb{R}^{\mathbb{N}},\gamma_\infty)$. The rates only depend on quantified holomorphy of (an analytic continuation of) the map $f$ to a product of strips in $\mathbb{C}^d$. As an application, we prove expression rate bounds of deep ReLU-NNs for response surfaces of elliptic PDEs with log-Gaussian random field inputs.