Embarrassingly Simple Scribble Supervision for 3D Medical Segmentation

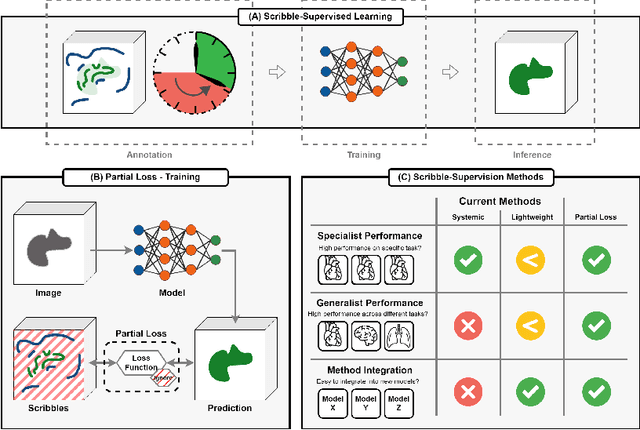
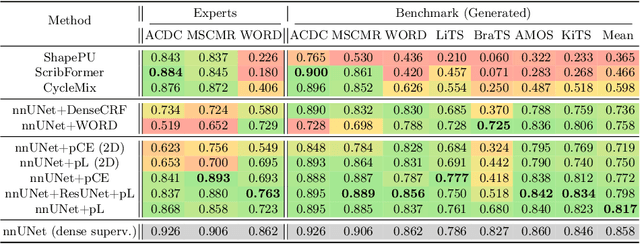
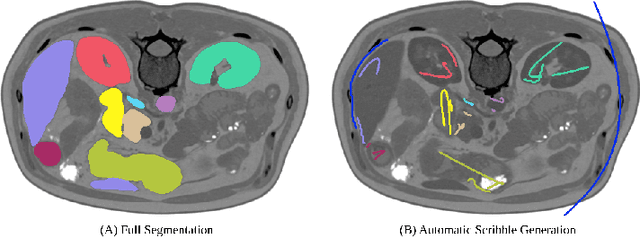
Traditionally, segmentation algorithms require dense annotations for training, demanding significant annotation efforts, particularly within the 3D medical imaging field. Scribble-supervised learning emerges as a possible solution to this challenge, promising a reduction in annotation efforts when creating large-scale datasets. Recently, a plethora of methods for optimized learning from scribbles have been proposed, but have so far failed to position scribble annotation as a beneficial alternative. We relate this shortcoming to two major issues: 1) the complex nature of many methods which deeply ties them to the underlying segmentation model, thus preventing a migration to more powerful state-of-the-art models as the field progresses and 2) the lack of a systematic evaluation to validate consistent performance across the broader medical domain, resulting in a lack of trust when applying these methods to new segmentation problems. To address these issues, we propose a comprehensive scribble supervision benchmark consisting of seven datasets covering a diverse set of anatomies and pathologies imaged with varying modalities. We furthermore propose the systematic use of partial losses, i.e. losses that are only computed on annotated voxels. Contrary to most existing methods, these losses can be seamlessly integrated into state-of-the-art segmentation methods, enabling them to learn from scribble annotations while preserving their original loss formulations. Our evaluation using nnU-Net reveals that while most existing methods suffer from a lack of generalization, the proposed approach consistently delivers state-of-the-art performance. Thanks to its simplicity, our approach presents an embarrassingly simple yet effective solution to the challenges of scribble supervision. Source code as well as our extensive scribble benchmarking suite will be made publicly available upon publication.

Benchmarking the CoW with the TopCoW Challenge: Topology-Aware Anatomical Segmentation of the Circle of Willis for CTA and MRA

The Circle of Willis (CoW) is an important network of arteries connecting major circulations of the brain. Its vascular architecture is believed to affect the risk, severity, and clinical outcome of serious neuro-vascular diseases. However, characterizing the highly variable CoW anatomy is still a manual and time-consuming expert task. The CoW is usually imaged by two angiographic imaging modalities, magnetic resonance angiography (MRA) and computed tomography angiography (CTA), but there exist limited public datasets with annotations on CoW anatomy, especially for CTA. Therefore we organized the TopCoW Challenge in 2023 with the release of an annotated CoW dataset and invited submissions worldwide for the CoW segmentation task, which attracted over 140 registered participants from four continents. TopCoW dataset was the first public dataset with voxel-level annotations for CoW's 13 vessel components, made possible by virtual-reality (VR) technology. It was also the first dataset with paired MRA and CTA from the same patients. TopCoW challenge aimed to tackle the CoW characterization problem as a multiclass anatomical segmentation task with an emphasis on topological metrics. The top performing teams managed to segment many CoW components to Dice scores around 90%, but with lower scores for communicating arteries and rare variants. There were also topological mistakes for predictions with high Dice scores. Additional topological analysis revealed further areas for improvement in detecting certain CoW components and matching CoW variant's topology accurately. TopCoW represented a first attempt at benchmarking the CoW anatomical segmentation task for MRA and CTA, both morphologically and topologically.

SAM.MD: Zero-shot medical image segmentation capabilities of the Segment Anything Model

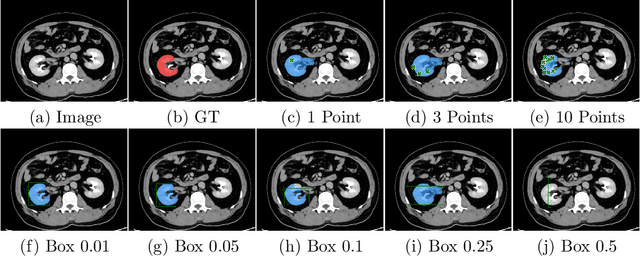
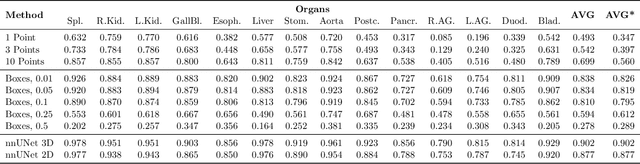
Foundation models have taken over natural language processing and image generation domains due to the flexibility of prompting. With the recent introduction of the Segment Anything Model (SAM), this prompt-driven paradigm has entered image segmentation with a hitherto unexplored abundance of capabilities. The purpose of this paper is to conduct an initial evaluation of the out-of-the-box zero-shot capabilities of SAM for medical image segmentation, by evaluating its performance on an abdominal CT organ segmentation task, via point or bounding box based prompting. We show that SAM generalizes well to CT data, making it a potential catalyst for the advancement of semi-automatic segmentation tools for clinicians. We believe that this foundation model, while not reaching state-of-the-art segmentation performance in our investigations, can serve as a highly potent starting point for further adaptations of such models to the intricacies of the medical domain. Keywords: medical image segmentation, SAM, foundation models, zero-shot learning

De Rham compatible Deep Neural Networks

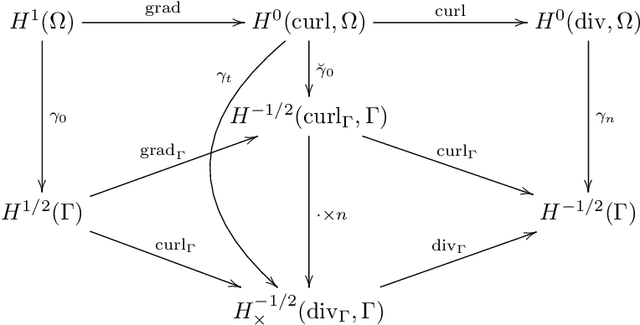
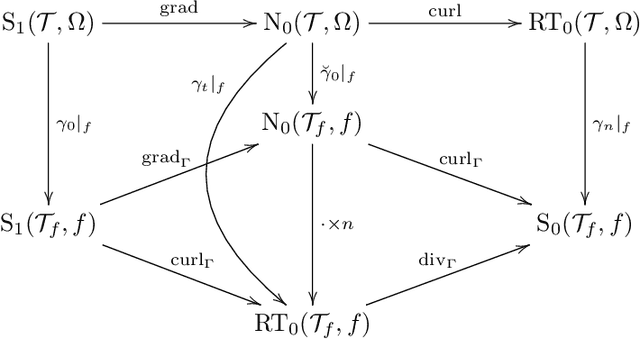
We construct several classes of neural networks with ReLU and BiSU (Binary Step Unit) activations, which exactly emulate the lowest order Finite Element (FE) spaces on regular, simplicial partitions of polygonal and polyhedral domains $\Omega \subset \mathbb{R}^d$, $d=2,3$. For continuous, piecewise linear (CPwL) functions, our constructions generalize previous results in that arbitrary, regular simplicial partitions of $\Omega$ are admitted, also in arbitrary dimension $d\geq 2$. Vector-valued elements emulated include the classical Raviart-Thomas and the first family of N\'{e}d\'{e}lec edge elements on triangles and tetrahedra. Neural Networks emulating these FE spaces are required in the correct approximation of boundary value problems of electromagnetism in nonconvex polyhedra $\Omega \subset \mathbb{R}^3$, thereby constituting an essential ingredient in the application of e.g. the methodology of ``physics-informed NNs'' or ``deep Ritz methods'' to electromagnetic field simulation via deep learning techniques. They satisfy exact (De Rham) sequence properties, and also spawn discrete boundary complexes on $\partial\Omega$ which satisfy exact sequence properties for the surface divergence and curl operators $\mathrm{div}_\Gamma$ and $\mathrm{curl}_\Gamma$, respectively, thereby enabling ``neural boundary elements'' for computational electromagnetism. We indicate generalizations of our constructions to higher-order compatible spaces and other, non-compatible classes of discretizations in particular the Crouzeix-Raviart elements and Hybridized, Higher Order (HHO) methods.