First Order System Least Squares Neural Networks

We introduce a conceptual framework for numerically solving linear elliptic, parabolic, and hyperbolic PDEs on bounded, polytopal domains in euclidean spaces by deep neural networks. The PDEs are recast as minimization of a least-squares (LSQ for short) residual of an equivalent, well-posed first-order system, over parametric families of deep neural networks. The associated LSQ residual is a) equal or proportional to a weak residual of the PDE, b) additive in terms of contributions from localized subnetworks, indicating locally ``out-of-equilibrium'' of neural networks with respect to the PDE residual, c) serves as numerical loss function for neural network training, and d) constitutes, even with incomplete training, a computable, (quasi-)optimal numerical error estimator in the context of adaptive LSQ finite element methods. In addition, an adaptive neural network growth strategy is proposed which, assuming exact numerical minimization of the LSQ loss functional, yields sequences of neural networks with realizations that converge rate-optimally to the exact solution of the first order system LSQ formulation.

Exponential Expressivity of ReLU$^k$ Neural Networks on Gevrey Classes with Point Singularities

We analyze deep Neural Network emulation rates of smooth functions with point singularities in bounded, polytopal domains $\mathrm{D} \subset \mathbb{R}^d$, $d=2,3$. We prove exponential emulation rates in Sobolev spaces in terms of the number of neurons and in terms of the number of nonzero coefficients for Gevrey-regular solution classes defined in terms of weighted Sobolev scales in $\mathrm{D}$, comprising the countably-normed spaces of I.M. Babu\v{s}ka and B.Q. Guo. As intermediate result, we prove that continuous, piecewise polynomial high order (``$p$-version'') finite elements with elementwise polynomial degree $p\in\mathbb{N}$ on arbitrary, regular, simplicial partitions of polyhedral domains $\mathrm{D} \subset \mathbb{R}^d$, $d\geq 2$ can be exactly emulated by neural networks combining ReLU and ReLU$^2$ activations. On shape-regular, simplicial partitions of polytopal domains $\mathrm{D}$, both the number of neurons and the number of nonzero parameters are proportional to the number of degrees of freedom of the finite element space, in particular for the $hp$-Finite Element Method of I.M. Babu\v{s}ka and B.Q. Guo.

Neural Networks for Singular Perturbations

We prove deep neural network (DNN for short) expressivity rate bounds for solution sets of a model class of singularly perturbed, elliptic two-point boundary value problems, in Sobolev norms, on the bounded interval $(-1,1)$. We assume that the given source term and reaction coefficient are analytic in $[-1,1]$. We establish expression rate bounds in Sobolev norms in terms of the NN size which are uniform with respect to the singular perturbation parameter for several classes of DNN architectures. In particular, ReLU NNs, spiking NNs, and $\tanh$- and sigmoid-activated NNs. The latter activations can represent ``exponential boundary layer solution features'' explicitly, in the last hidden layer of the DNN, i.e. in a shallow subnetwork, and afford improved robust expression rate bounds in terms of the NN size. We prove that all DNN architectures allow robust exponential solution expression in so-called `energy' as well as in `balanced' Sobolev norms, for analytic input data.

Deep ReLU networks and high-order finite element methods II: Chebyshev emulation

Expression rates and stability in Sobolev norms of deep ReLU neural networks (NNs) in terms of the number of parameters defining the NN for continuous, piecewise polynomial functions, on arbitrary, finite partitions $\mathcal{T}$ of a bounded interval $(a,b)$ are addressed. Novel constructions of ReLU NN surrogates encoding the approximated functions in terms of Chebyshev polynomial expansion coefficients are developed. Chebyshev coefficients can be computed easily from the values of the function in the Clenshaw--Curtis points using the inverse fast Fourier transform. Bounds on expression rates and stability that are superior to those of constructions based on ReLU NN emulations of monomials considered in [Opschoor, Petersen, Schwab, 2020] are obtained. All emulation bounds are explicit in terms of the (arbitrary) partition of the interval, the target emulation accuracy and the polynomial degree in each element of the partition. ReLU NN emulation error estimates are provided for various classes of functions and norms, commonly encountered in numerical analysis. In particular, we show exponential ReLU emulation rate bounds for analytic functions with point singularities and develop an interface between Chebfun approximations and constructive ReLU NN emulations.

Deep Operator Network Approximation Rates for Lipschitz Operators

We establish universality and expression rate bounds for a class of neural Deep Operator Networks (DON) emulating Lipschitz (or H\"older) continuous maps $\mathcal G:\mathcal X\to\mathcal Y$ between (subsets of) separable Hilbert spaces $\mathcal X$, $\mathcal Y$. The DON architecture considered uses linear encoders $\mathcal E$ and decoders $\mathcal D$ via (biorthogonal) Riesz bases of $\mathcal X$, $\mathcal Y$, and an approximator network of an infinite-dimensional, parametric coordinate map that is Lipschitz continuous on the sequence space $\ell^2(\mathbb N)$. Unlike previous works ([Herrmann, Schwab and Zech: Neural and Spectral operator surrogates: construction and expression rate bounds, SAM Report, 2022], [Marcati and Schwab: Exponential Convergence of Deep Operator Networks for Elliptic Partial Differential Equations, SAM Report, 2022]), which required for example $\mathcal G$ to be holomorphic, the present expression rate results require mere Lipschitz (or H\"older) continuity of $\mathcal G$. Key in the proof of the present expression rate bounds is the use of either super-expressive activations (e.g. [Yarotski: Elementary superexpressive activations, Int. Conf. on ML, 2021], [Shen, Yang and Zhang: Neural network approximation: Three hidden layers are enough, Neural Networks, 2021], and the references there) which are inspired by the Kolmogorov superposition theorem, or of nonstandard NN architectures with standard (ReLU) activations as recently proposed in [Zhang, Shen and Yang: Neural Network Architecture Beyond Width and Depth, Adv. in Neural Inf. Proc. Sys., 2022]. We illustrate the abstract results by approximation rate bounds for emulation of a) solution operators for parametric elliptic variational inequalities, and b) Lipschitz maps of Hilbert-Schmidt operators.

Neural and gpc operator surrogates: construction and expression rate bounds

Approximation rates are analyzed for deep surrogates of maps between infinite-dimensional function spaces, arising e.g. as data-to-solution maps of linear and nonlinear partial differential equations. Specifically, we study approximation rates for Deep Neural Operator and Generalized Polynomial Chaos (gpc) Operator surrogates for nonlinear, holomorphic maps between infinite-dimensional, separable Hilbert spaces. Operator in- and outputs from function spaces are assumed to be parametrized by stable, affine representation systems. Admissible representation systems comprise orthonormal bases, Riesz bases or suitable tight frames of the spaces under consideration. Algebraic expression rate bounds are established for both, deep neural and gpc operator surrogates acting in scales of separable Hilbert spaces containing domain and range of the map to be expressed, with finite Sobolev or Besov regularity. We illustrate the abstract concepts by expression rate bounds for the coefficient-to-solution map for a linear elliptic PDE on the torus.

De Rham compatible Deep Neural Networks

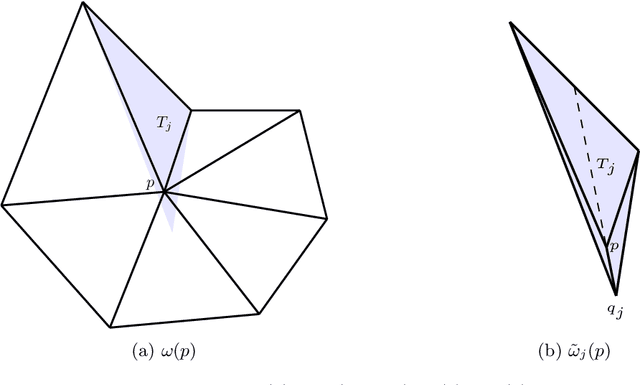
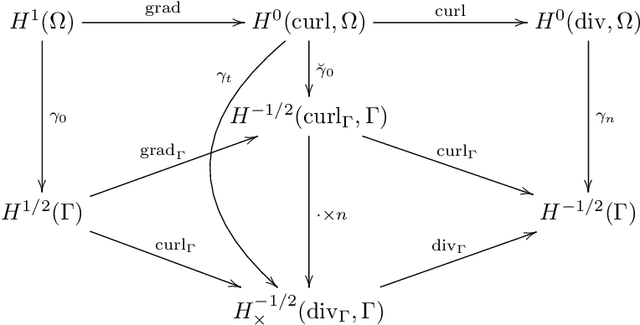
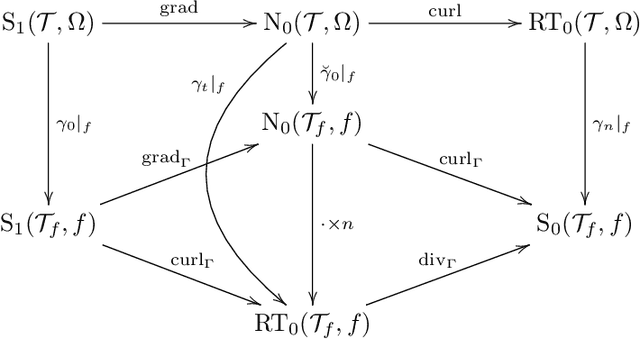
We construct several classes of neural networks with ReLU and BiSU (Binary Step Unit) activations, which exactly emulate the lowest order Finite Element (FE) spaces on regular, simplicial partitions of polygonal and polyhedral domains $\Omega \subset \mathbb{R}^d$, $d=2,3$. For continuous, piecewise linear (CPwL) functions, our constructions generalize previous results in that arbitrary, regular simplicial partitions of $\Omega$ are admitted, also in arbitrary dimension $d\geq 2$. Vector-valued elements emulated include the classical Raviart-Thomas and the first family of N\'{e}d\'{e}lec edge elements on triangles and tetrahedra. Neural Networks emulating these FE spaces are required in the correct approximation of boundary value problems of electromagnetism in nonconvex polyhedra $\Omega \subset \mathbb{R}^3$, thereby constituting an essential ingredient in the application of e.g. the methodology of ``physics-informed NNs'' or ``deep Ritz methods'' to electromagnetic field simulation via deep learning techniques. They satisfy exact (De Rham) sequence properties, and also spawn discrete boundary complexes on $\partial\Omega$ which satisfy exact sequence properties for the surface divergence and curl operators $\mathrm{div}_\Gamma$ and $\mathrm{curl}_\Gamma$, respectively, thereby enabling ``neural boundary elements'' for computational electromagnetism. We indicate generalizations of our constructions to higher-order compatible spaces and other, non-compatible classes of discretizations in particular the Crouzeix-Raviart elements and Hybridized, Higher Order (HHO) methods.

Exponential Convergence of Deep Operator Networks for Elliptic Partial Differential Equations

We construct deep operator networks (ONets) between infinite-dimensional spaces that emulate with an exponential rate of convergence the coefficient-to-solution map of elliptic second-order PDEs. In particular, we consider problems set in $d$-dimensional periodic domains, $d=1, 2, \dots$, and with analytic right-hand sides and coefficients. Our analysis covers diffusion-reaction problems, parametric diffusion equations, and elliptic systems such as linear isotropic elastostatics in heterogeneous materials. We leverage the exponential convergence of spectral collocation methods for boundary value problems whose solutions are analytic. In the present periodic and analytic setting, this follows from classical elliptic regularity. Within the ONet branch and trunk construction of [Chen and Chen, 1993] and of [Lu et al., 2021], we show the existence of deep ONets which emulate the coefficient-to-solution map to accuracy $\varepsilon>0$ in the $H^1$ norm, uniformly over the coefficient set. We prove that the neural networks in the ONet have size $\mathcal{O}(\left|\log(\varepsilon)\right|^\kappa)$ for some $\kappa>0$ depending on the physical space dimension.

Deep Learning in High Dimension: Neural Network Approximation of Analytic Functions in $L^2(\mathbb{R}^d,γ_d)$

For artificial deep neural networks, we prove expression rates for analytic functions $f:\mathbb{R}^d\to\mathbb{R}$ in the norm of $L^2(\mathbb{R}^d,\gamma_d)$ where $d\in {\mathbb{N}}\cup\{ \infty \}$. Here $\gamma_d$ denotes the Gaussian product probability measure on $\mathbb{R}^d$. We consider in particular ReLU and ReLU${}^k$ activations for integer $k\geq 2$. For $d\in\mathbb{N}$, we show exponential convergence rates in $L^2(\mathbb{R}^d,\gamma_d)$. In case $d=\infty$, under suitable smoothness and sparsity assumptions on $f:\mathbb{R}^{\mathbb{N}}\to\mathbb{R}$, with $\gamma_\infty$ denoting an infinite (Gaussian) product measure on $\mathbb{R}^{\mathbb{N}}$, we prove dimension-independent expression rate bounds in the norm of $L^2(\mathbb{R}^{\mathbb{N}},\gamma_\infty)$. The rates only depend on quantified holomorphy of (an analytic continuation of) the map $f$ to a product of strips in $\mathbb{C}^d$. As an application, we prove expression rate bounds of deep ReLU-NNs for response surfaces of elliptic PDEs with log-Gaussian random field inputs.

Exponential ReLU Neural Network Approximation Rates for Point and Edge Singularities

We prove exponential expressivity with stable ReLU Neural Networks (ReLU NNs) in $H^1(\Omega)$ for weighted analytic function classes in certain polytopal domains $\Omega$, in space dimension $d=2,3$. Functions in these classes are locally analytic on open subdomains $D\subset \Omega$, but may exhibit isolated point singularities in the interior of $\Omega$ or corner and edge singularities at the boundary $\partial \Omega$. The exponential expression rate bounds proved here imply uniform exponential expressivity by ReLU NNs of solution families for several elliptic boundary and eigenvalue problems with analytic data. The exponential approximation rates are shown to hold in space dimension $d = 2$ on Lipschitz polygons with straight sides, and in space dimension $d=3$ on Fichera-type polyhedral domains with plane faces. The constructive proofs indicate in particular that NN depth and size increase poly-logarithmically with respect to the target NN approximation accuracy $\varepsilon>0$ in $H^1(\Omega)$. The results cover in particular solution sets of linear, second order elliptic PDEs with analytic data and certain nonlinear elliptic eigenvalue problems with analytic nonlinearities and singular, weighted analytic potentials as arise in electron structure models. In the latter case, the functions correspond to electron densities that exhibit isolated point singularities at the positions of the nuclei. Our findings provide in particular mathematical foundation of recently reported, successful uses of deep neural networks in variational electron structure algorithms.