Marcello Longo
De Rham compatible Deep Neural Networks
Jan 14, 2022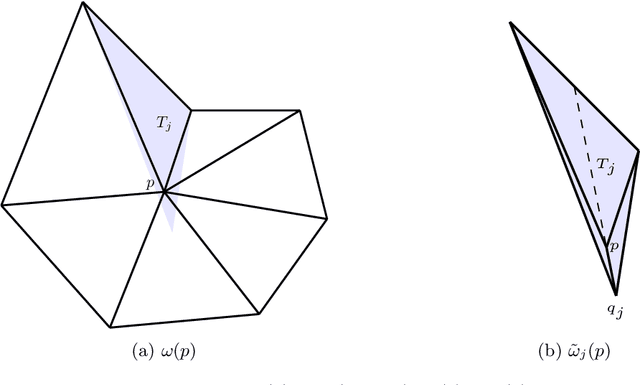
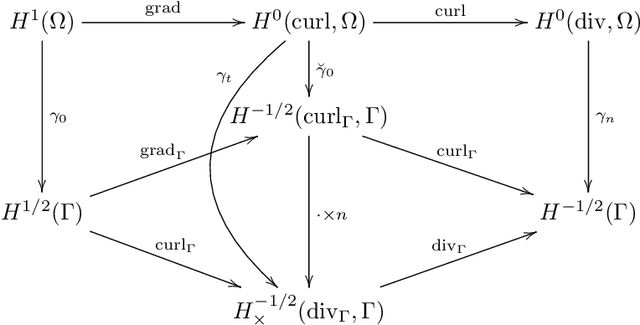
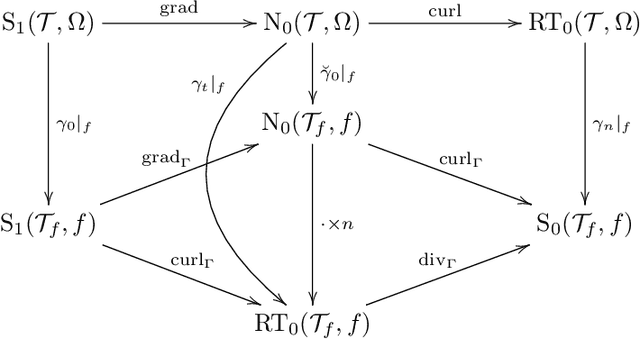
Abstract:We construct several classes of neural networks with ReLU and BiSU (Binary Step Unit) activations, which exactly emulate the lowest order Finite Element (FE) spaces on regular, simplicial partitions of polygonal and polyhedral domains $\Omega \subset \mathbb{R}^d$, $d=2,3$. For continuous, piecewise linear (CPwL) functions, our constructions generalize previous results in that arbitrary, regular simplicial partitions of $\Omega$ are admitted, also in arbitrary dimension $d\geq 2$. Vector-valued elements emulated include the classical Raviart-Thomas and the first family of N\'{e}d\'{e}lec edge elements on triangles and tetrahedra. Neural Networks emulating these FE spaces are required in the correct approximation of boundary value problems of electromagnetism in nonconvex polyhedra $\Omega \subset \mathbb{R}^3$, thereby constituting an essential ingredient in the application of e.g. the methodology of ``physics-informed NNs'' or ``deep Ritz methods'' to electromagnetic field simulation via deep learning techniques. They satisfy exact (De Rham) sequence properties, and also spawn discrete boundary complexes on $\partial\Omega$ which satisfy exact sequence properties for the surface divergence and curl operators $\mathrm{div}_\Gamma$ and $\mathrm{curl}_\Gamma$, respectively, thereby enabling ``neural boundary elements'' for computational electromagnetism. We indicate generalizations of our constructions to higher-order compatible spaces and other, non-compatible classes of discretizations in particular the Crouzeix-Raviart elements and Hybridized, Higher Order (HHO) methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge