Convergence results for projected line-search methods on varieties of low-rank matrices via Łojasiewicz inequality
Paper and Code
Apr 22, 2015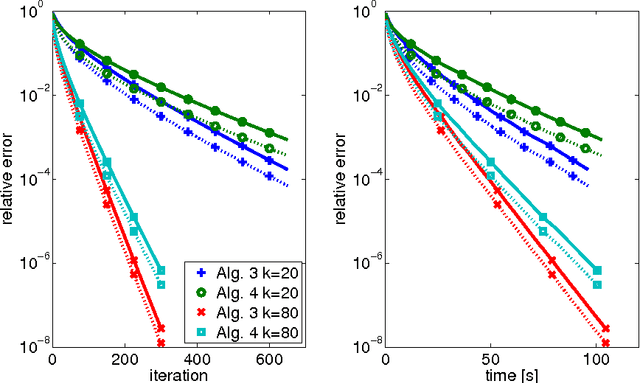
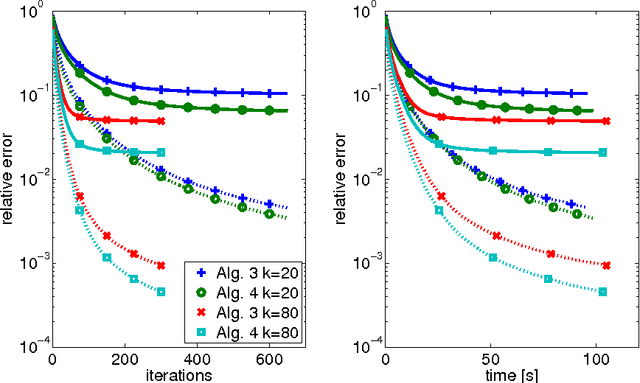
The aim of this paper is to derive convergence results for projected line-search methods on the real-algebraic variety $\mathcal{M}_{\le k}$ of real $m \times n$ matrices of rank at most $k$. Such methods extend Riemannian optimization methods, which are successfully used on the smooth manifold $\mathcal{M}_k$ of rank-$k$ matrices, to its closure by taking steps along gradient-related directions in the tangent cone, and afterwards projecting back to $\mathcal{M}_{\le k}$. Considering such a method circumvents the difficulties which arise from the nonclosedness and the unbounded curvature of $\mathcal{M}_k$. The pointwise convergence is obtained for real-analytic functions on the basis of a \L{}ojasiewicz inequality for the projection of the antigradient to the tangent cone. If the derived limit point lies on the smooth part of $\mathcal{M}_{\le k}$, i.e. in $\mathcal{M}_k$, this boils down to more or less known results, but with the benefit that asymptotic convergence rate estimates (for specific step-sizes) can be obtained without an a priori curvature bound, simply from the fact that the limit lies on a smooth manifold. At the same time, one can give a convincing justification for assuming critical points to lie in $\mathcal{M}_k$: if $X$ is a critical point of $f$ on $\mathcal{M}_{\le k}$, then either $X$ has rank $k$, or $\nabla f(X) = 0$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge