Hardness of Deceptive Certificate Selection

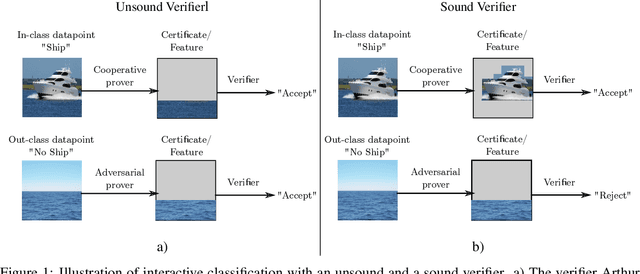
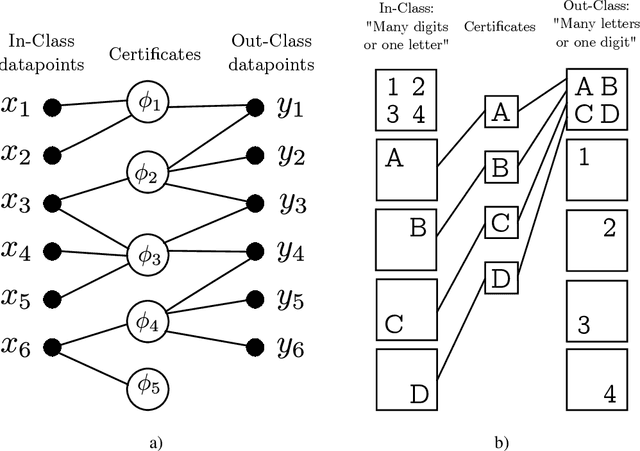
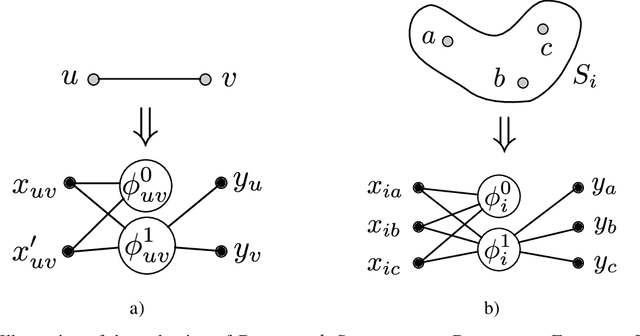
Recent progress towards theoretical interpretability guarantees for AI has been made with classifiers that are based on interactive proof systems. A prover selects a certificate from the datapoint and sends it to a verifier who decides the class. In the context of machine learning, such a certificate can be a feature that is informative of the class. For a setup with high soundness and completeness, the exchanged certificates must have a high mutual information with the true class of the datapoint. However, this guarantee relies on a bound on the Asymmetric Feature Correlation of the dataset, a property that so far is difficult to estimate for high-dimensional data. It was conjectured in W\"aldchen et al. that it is computationally hard to exploit the AFC, which is what we prove here. We consider a malicious prover-verifier duo that aims to exploit the AFC to achieve high completeness and soundness while using uninformative certificates. We show that this task is $\mathsf{NP}$-hard and cannot be approximated better than $\mathcal{O}(m^{1/8 - \epsilon})$, where $m$ is the number of possible certificates, for $\epsilon>0$ under the Dense-vs-Random conjecture. This is some evidence that AFC should not prevent the use of interactive classification for real-world tasks, as it is computationally hard to be exploited.

Merlin-Arthur Classifiers: Formal Interpretability with Interactive Black Boxes

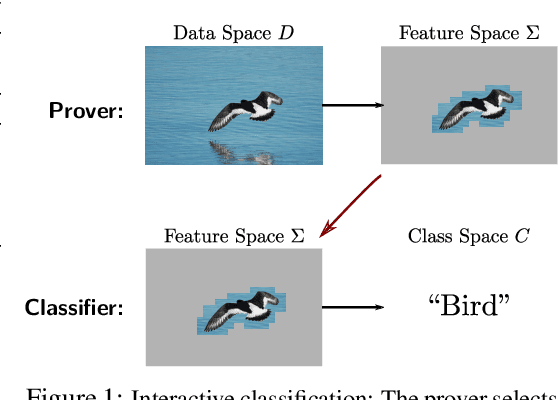
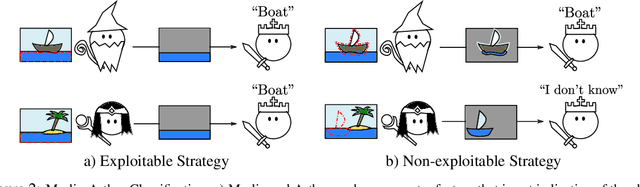
We present a new theoretical framework for making black box classifiers such as Neural Networks interpretable, basing our work on clear assumptions and guarantees. In our setting, which is inspired by the Merlin-Arthur protocol from Interactive Proof Systems, two functions cooperate to achieve a classification together: the \emph{prover} selects a small set of features as a certificate and presents it to the \emph{classifier}. Including a second, adversarial prover allows us to connect a game-theoretic equilibrium to information-theoretic guarantees on the exchanged features. We define notions of completeness and soundness that enable us to lower bound the mutual information between features and class. To demonstrate good agreement between theory and practice, we support our framework by providing numerical experiments for Neural Network classifiers, explicitly calculating the mutual information of features with respect to the class.

Training Characteristic Functions with Reinforcement Learning: XAI-methods play Connect Four

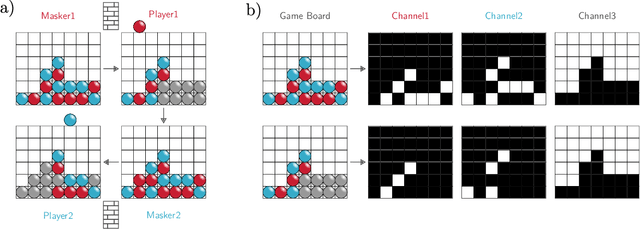
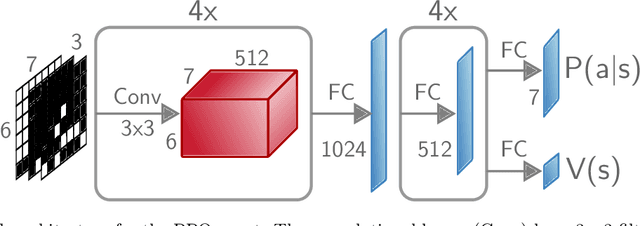
One of the goals of Explainable AI (XAI) is to determine which input components were relevant for a classifier decision. This is commonly know as saliency attribution. Characteristic functions (from cooperative game theory) are able to evaluate partial inputs and form the basis for theoretically "fair" attribution methods like Shapley values. Given only a standard classifier function, it is unclear how partial input should be realised. Instead, most XAI-methods for black-box classifiers like neural networks consider counterfactual inputs that generally lie off-manifold. This makes them hard to evaluate and easy to manipulate. We propose a setup to directly train characteristic functions in the form of neural networks to play simple two-player games. We apply this to the game of Connect Four by randomly hiding colour information from our agents during training. This has three advantages for comparing XAI-methods: It alleviates the ambiguity about how to realise partial input, makes off-manifold evaluation unnecessary and allows us to compare the methods by letting them play against each other.

A Complete Characterisation of ReLU-Invariant Distributions

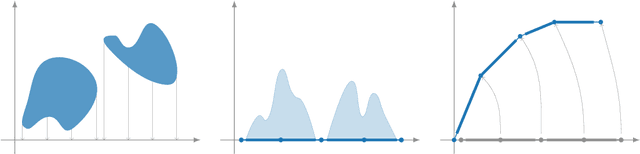
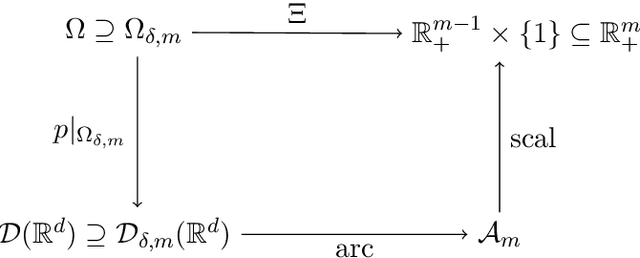
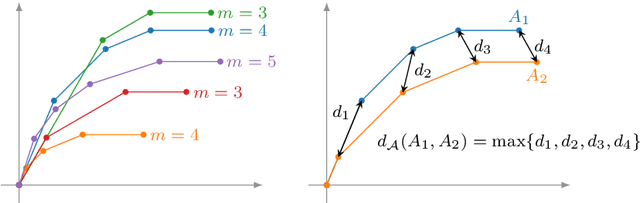
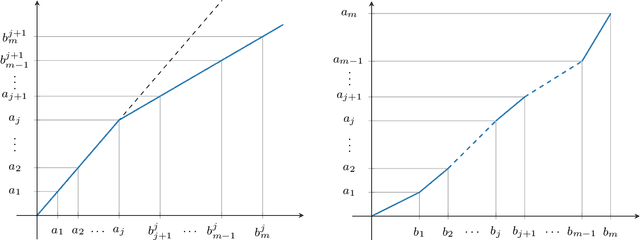
We give a complete characterisation of families of probability distributions that are invariant under the action of ReLU neural network layers. The need for such families arises during the training of Bayesian networks or the analysis of trained neural networks, e.g., in the context of uncertainty quantification (UQ) or explainable artificial intelligence (XAI). We prove that no invariant parametrised family of distributions can exist unless at least one of the following three restrictions holds: First, the network layers have a width of one, which is unreasonable for practical neural networks. Second, the probability measures in the family have finite support, which basically amounts to sampling distributions. Third, the parametrisation of the family is not locally Lipschitz continuous, which excludes all computationally feasible families. Finally, we show that these restrictions are individually necessary. For each of the three cases we can construct an invariant family exploiting exactly one of the restrictions but not the other two.

A Rate-Distortion Framework for Explaining Neural Network Decisions

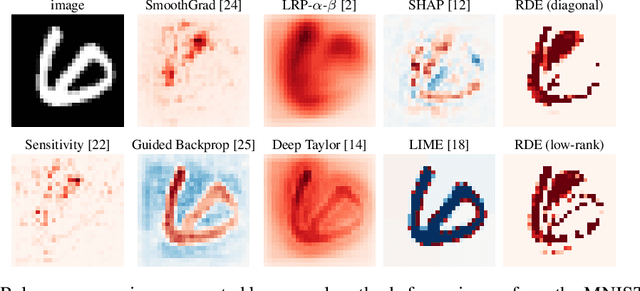
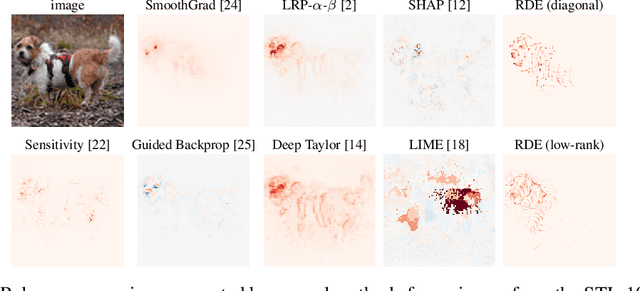
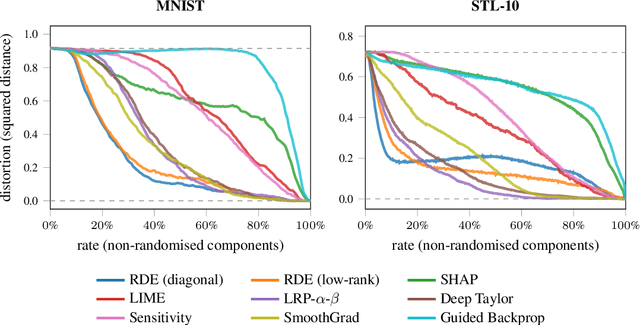
We formalise the widespread idea of interpreting neural network decisions as an explicit optimisation problem in a rate-distortion framework. A set of input features is deemed relevant for a classification decision if the expected classifier score remains nearly constant when randomising the remaining features. We discuss the computational complexity of finding small sets of relevant features and show that the problem is complete for $\mathsf{NP}^\mathsf{PP}$, an important class of computational problems frequently arising in AI tasks. Furthermore, we show that it even remains $\mathsf{NP}$-hard to only approximate the optimal solution to within any non-trivial approximation factor. Finally, we consider a continuous problem relaxation and develop a heuristic solution strategy based on assumed density filtering for deep ReLU neural networks. We present numerical experiments for two image classification data sets where we outperform established methods in particular for sparse explanations of neural network decisions.

Unmasking Clever Hans Predictors and Assessing What Machines Really Learn

Current learning machines have successfully solved hard application problems, reaching high accuracy and displaying seemingly "intelligent" behavior. Here we apply recent techniques for explaining decisions of state-of-the-art learning machines and analyze various tasks from computer vision and arcade games. This showcases a spectrum of problem-solving behaviors ranging from naive and short-sighted, to well-informed and strategic. We observe that standard performance evaluation metrics can be oblivious to distinguishing these diverse problem solving behaviors. Furthermore, we propose our semi-automated Spectral Relevance Analysis that provides a practically effective way of characterizing and validating the behavior of nonlinear learning machines. This helps to assess whether a learned model indeed delivers reliably for the problem that it was conceived for. Furthermore, our work intends to add a voice of caution to the ongoing excitement about machine intelligence and pledges to evaluate and judge some of these recent successes in a more nuanced manner.