Feature-Based Interpretable Optimization

For optimization models to be used in practice, it is crucial that users trust the results. A key factor in this aspect is the interpretability of the solution process. A previous framework for inherently interpretable optimization models used decision trees to map instances to solutions of the underlying optimization model. Based on this work, we investigate how we can use more general optimization rules to further increase interpretability and at the same time give more freedom to the decision maker. The proposed rules do not map to a concrete solution but to a set of solutions characterized by common features. To find such optimization rules, we present an exact methodology using mixed-integer programming formulations as well as heuristics. We also outline the challenges and opportunities that these methods present. In particular, we demonstrate the improvement in solution quality that our approach offers compared to existing frameworks for interpretable optimization and we discuss the relationship between interpretability and performance. These findings are supported by experiments using both synthetic and real-world data.

Merlin-Arthur Classifiers: Formal Interpretability with Interactive Black Boxes

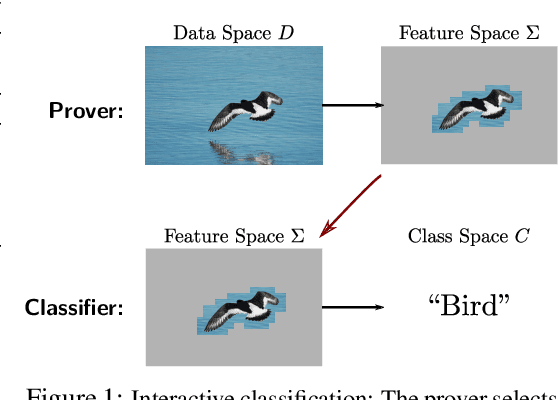
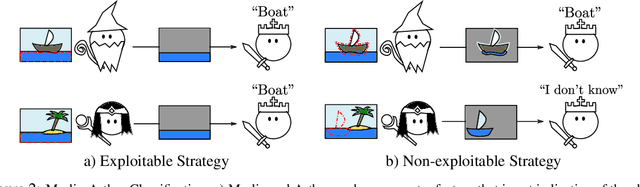
We present a new theoretical framework for making black box classifiers such as Neural Networks interpretable, basing our work on clear assumptions and guarantees. In our setting, which is inspired by the Merlin-Arthur protocol from Interactive Proof Systems, two functions cooperate to achieve a classification together: the \emph{prover} selects a small set of features as a certificate and presents it to the \emph{classifier}. Including a second, adversarial prover allows us to connect a game-theoretic equilibrium to information-theoretic guarantees on the exchanged features. We define notions of completeness and soundness that enable us to lower bound the mutual information between features and class. To demonstrate good agreement between theory and practice, we support our framework by providing numerical experiments for Neural Network classifiers, explicitly calculating the mutual information of features with respect to the class.