Towards Robust Interpretable Surrogates for Optimization

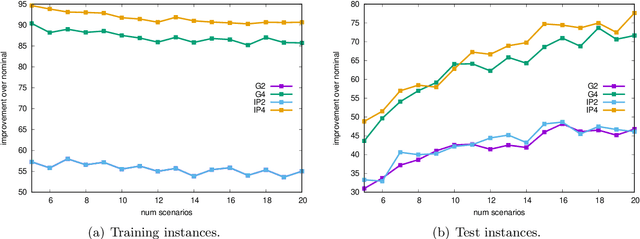
An important factor in the practical implementation of optimization models is the acceptance by the intended users. This is influenced among other factors by the interpretability of the solution process. Decision rules that meet this requirement can be generated using the framework for inherently interpretable optimization models. In practice, there is often uncertainty about the parameters of an optimization problem. An established way to deal with this challenge is the concept of robust optimization. The goal of our work is to combine both concepts: to create decision trees as surrogates for the optimization process that are more robust to perturbations and still inherently interpretable. For this purpose we present suitable models based on different variants to model uncertainty, and solution methods. Furthermore, the applicability of heuristic methods to perform this task is evaluated. Both approaches are compared with the existing framework for inherently interpretable optimization models.

Feature-Based Interpretable Optimization

For optimization models to be used in practice, it is crucial that users trust the results. A key factor in this aspect is the interpretability of the solution process. A previous framework for inherently interpretable optimization models used decision trees to map instances to solutions of the underlying optimization model. Based on this work, we investigate how we can use more general optimization rules to further increase interpretability and at the same time give more freedom to the decision maker. The proposed rules do not map to a concrete solution but to a set of solutions characterized by common features. To find such optimization rules, we present an exact methodology using mixed-integer programming formulations as well as heuristics. We also outline the challenges and opportunities that these methods present. In particular, we demonstrate the improvement in solution quality that our approach offers compared to existing frameworks for interpretable optimization and we discuss the relationship between interpretability and performance. These findings are supported by experiments using both synthetic and real-world data.

A Framework for Data-Driven Explainability in Mathematical Optimization

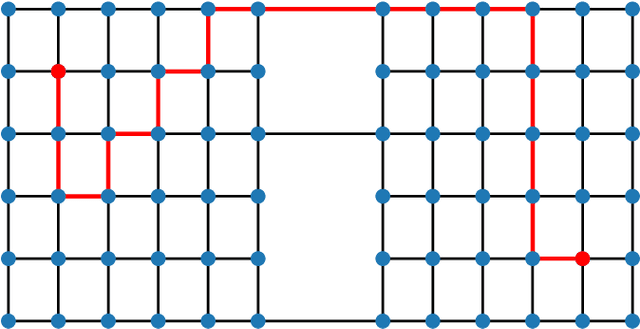
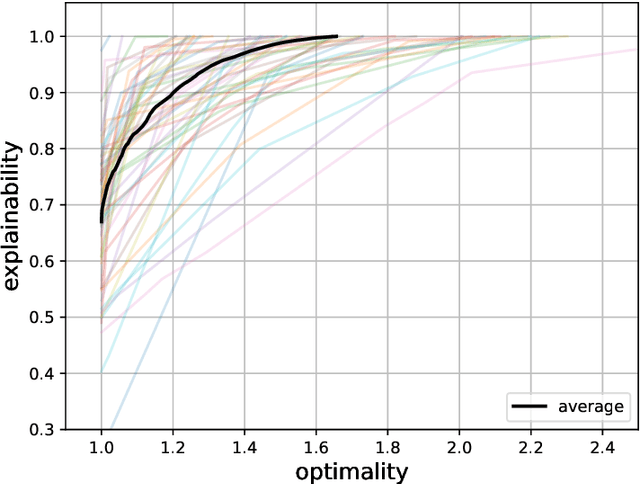
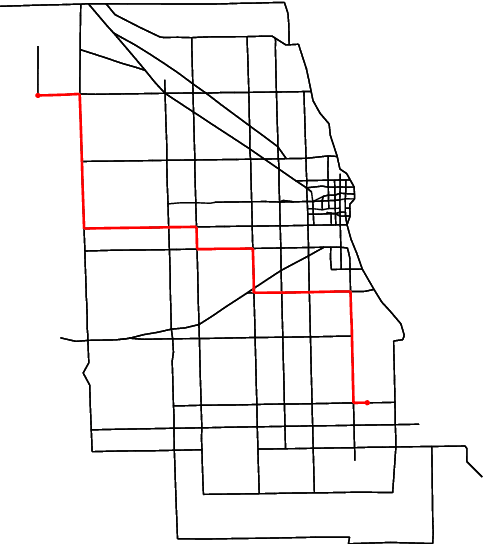
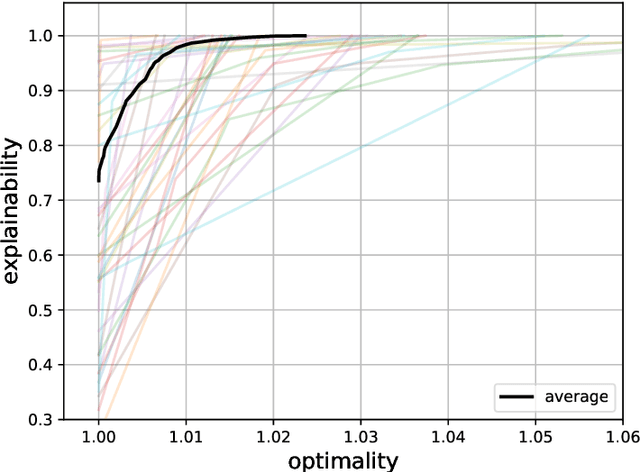
Advancements in mathematical programming have made it possible to efficiently tackle large-scale real-world problems that were deemed intractable just a few decades ago. However, provably optimal solutions may not be accepted due to the perception of optimization software as a black box. Although well understood by scientists, this lacks easy accessibility for practitioners. Hence, we advocate for introducing the explainability of a solution as another evaluation criterion, next to its objective value, which enables us to find trade-off solutions between these two criteria. Explainability is attained by comparing against (not necessarily optimal) solutions that were implemented in similar situations in the past. Thus, solutions are preferred that exhibit similar features. Although we prove that already in simple cases the explainable model is NP-hard, we characterize relevant polynomially solvable cases such as the explainable shortest-path problem. Our numerical experiments on both artificial as well as real-world road networks show the resulting Pareto front. It turns out that the cost of enforcing explainability can be very small.

A Framework for Inherently Interpretable Optimization Models

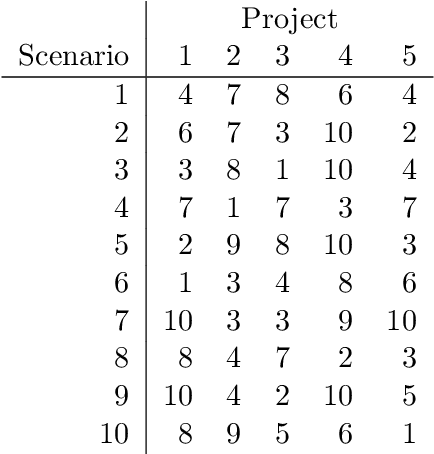
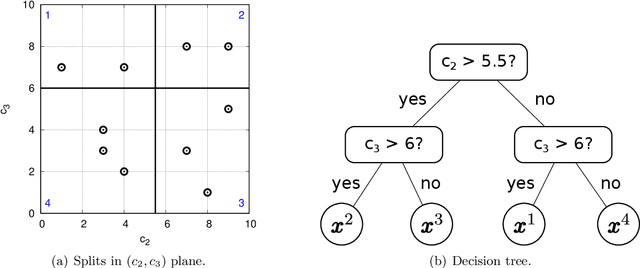
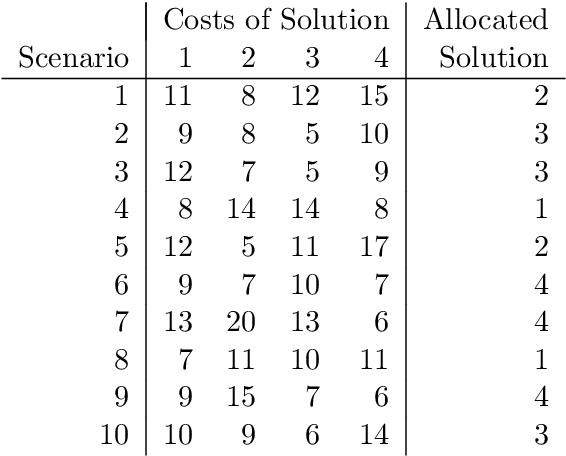
With dramatic improvements in optimization software, the solution of large-scale problems that seemed intractable decades ago are now a routine task. This puts even more real-world applications into the reach of optimizers. At the same time, solving optimization problems often turns out to be one of the smaller difficulties when putting solutions into practice. One major barrier is that the optimization software can be perceived as a black box, which may produce solutions of high quality, but can create completely different solutions when circumstances change leading to low acceptance of optimized solutions. Such issues of interpretability and explainability have seen significant attention in other areas, such as machine learning, but less so in optimization. In this paper we propose an optimization framework to derive solutions that inherently come with an easily comprehensible explanatory rule, under which circumstances which solution should be chosen. Focussing on decision trees to represent explanatory rules, we propose integer programming formulations as well as a heuristic method that ensure applicability of our approach even for large-scale problems. Computational experiments using random and real-world data indicate that the costs of inherent interpretability can be very small.

Game Tree Search in a Robust Multistage Optimization Framework: Exploiting Pruning Mechanisms

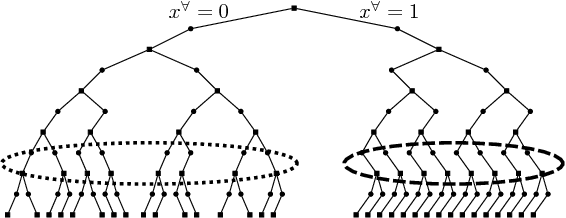
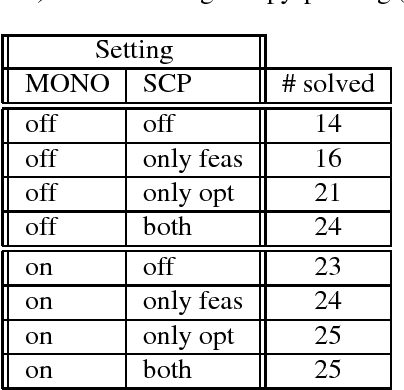
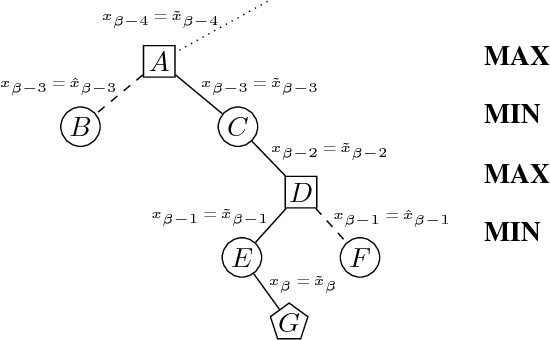
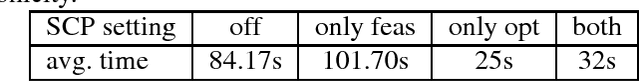
We investigate pruning in search trees of so-called quantified integer linear programs (QIPs). QIPs consist of a set of linear inequalities and a minimax objective function, where some variables are existentially and others are universally quantified. They can be interpreted as two-person zero-sum games between an existential and a universal player on the one hand, or multistage optimization problems under uncertainty on the other hand. Solutions are so-called winning strategies for the existential player that specify how to react on moves of the universal player - i.e. certain assignments of universally quantified variables - to certainly win the game. QIPs can be solved with the help of game tree search that is enhanced with non-chronological back-jumping. We develop and theoretically substantiate pruning techniques based upon (algebraic) properties similar to pruning mechanisms known from linear programming and quantified boolean formulas. The presented Strategic Copy-Pruning mechanism allows to \textit{implicitly} deduce the existence of a strategy in linear time (by static examination of the QIP-matrix) without explicitly traversing the strategy itself. We show that the implementation of our findings can massively speed up the search process.