A Framework for Inherently Interpretable Optimization Models
Paper and Code
Aug 26, 2022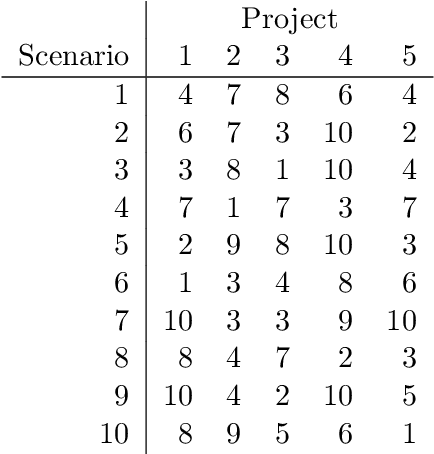
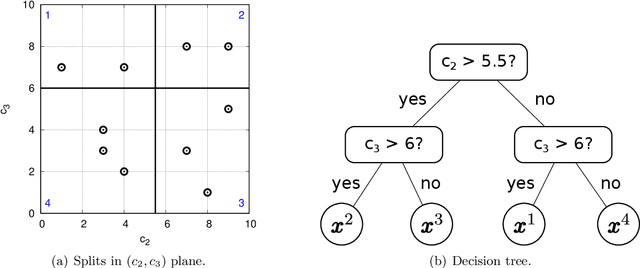
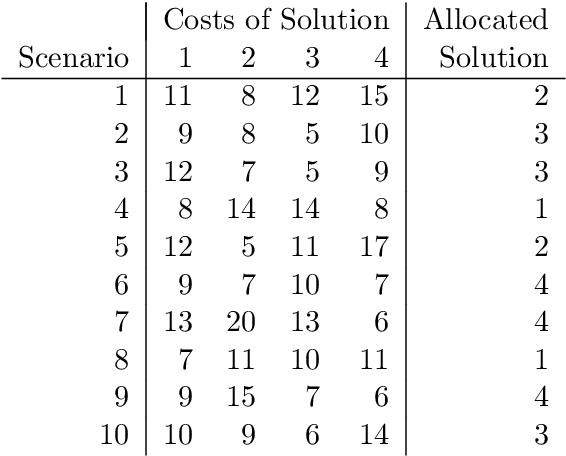
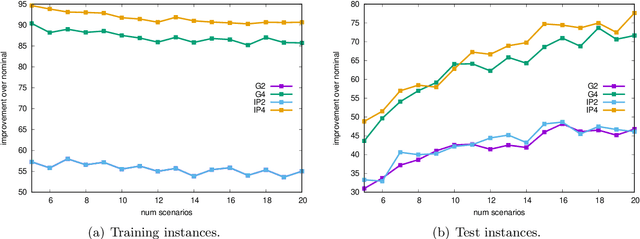
With dramatic improvements in optimization software, the solution of large-scale problems that seemed intractable decades ago are now a routine task. This puts even more real-world applications into the reach of optimizers. At the same time, solving optimization problems often turns out to be one of the smaller difficulties when putting solutions into practice. One major barrier is that the optimization software can be perceived as a black box, which may produce solutions of high quality, but can create completely different solutions when circumstances change leading to low acceptance of optimized solutions. Such issues of interpretability and explainability have seen significant attention in other areas, such as machine learning, but less so in optimization. In this paper we propose an optimization framework to derive solutions that inherently come with an easily comprehensible explanatory rule, under which circumstances which solution should be chosen. Focussing on decision trees to represent explanatory rules, we propose integer programming formulations as well as a heuristic method that ensure applicability of our approach even for large-scale problems. Computational experiments using random and real-world data indicate that the costs of inherent interpretability can be very small.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge