Towards Robust Interpretable Surrogates for Optimization

An important factor in the practical implementation of optimization models is the acceptance by the intended users. This is influenced among other factors by the interpretability of the solution process. Decision rules that meet this requirement can be generated using the framework for inherently interpretable optimization models. In practice, there is often uncertainty about the parameters of an optimization problem. An established way to deal with this challenge is the concept of robust optimization. The goal of our work is to combine both concepts: to create decision trees as surrogates for the optimization process that are more robust to perturbations and still inherently interpretable. For this purpose we present suitable models based on different variants to model uncertainty, and solution methods. Furthermore, the applicability of heuristic methods to perform this task is evaluated. Both approaches are compared with the existing framework for inherently interpretable optimization models.

Feature-Based Interpretable Optimization

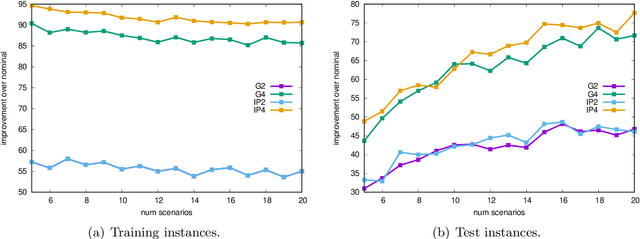
For optimization models to be used in practice, it is crucial that users trust the results. A key factor in this aspect is the interpretability of the solution process. A previous framework for inherently interpretable optimization models used decision trees to map instances to solutions of the underlying optimization model. Based on this work, we investigate how we can use more general optimization rules to further increase interpretability and at the same time give more freedom to the decision maker. The proposed rules do not map to a concrete solution but to a set of solutions characterized by common features. To find such optimization rules, we present an exact methodology using mixed-integer programming formulations as well as heuristics. We also outline the challenges and opportunities that these methods present. In particular, we demonstrate the improvement in solution quality that our approach offers compared to existing frameworks for interpretable optimization and we discuss the relationship between interpretability and performance. These findings are supported by experiments using both synthetic and real-world data.

A Framework for Data-Driven Explainability in Mathematical Optimization

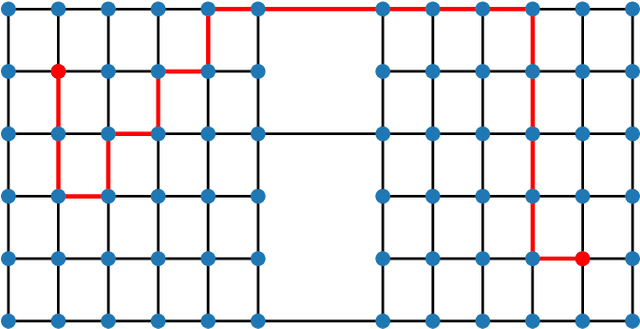
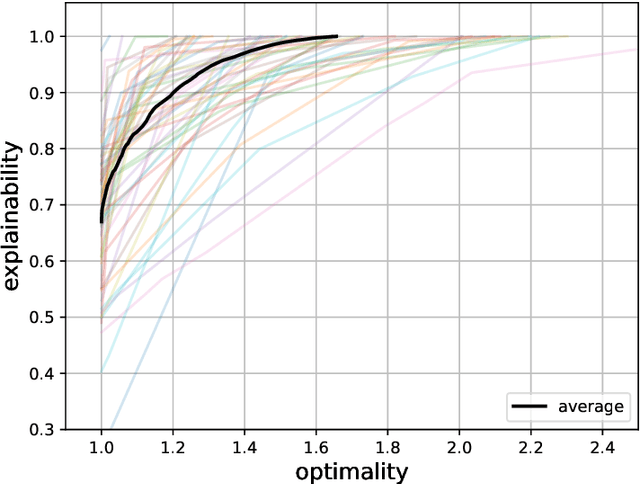
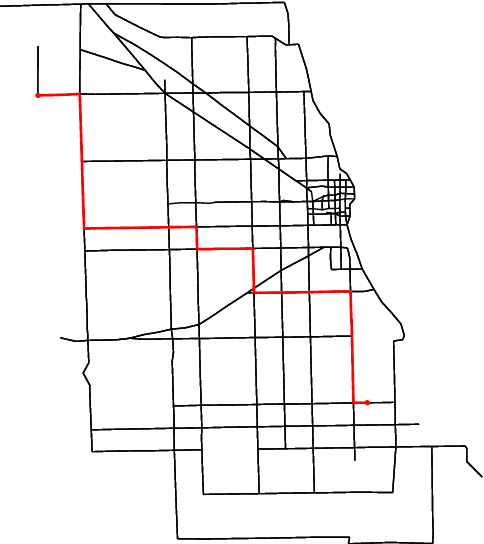
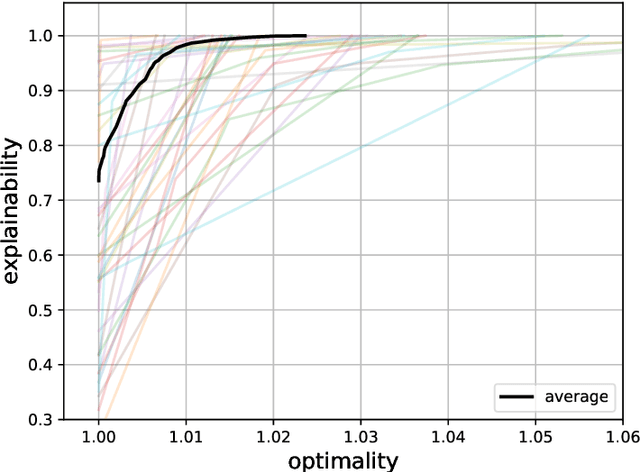
Advancements in mathematical programming have made it possible to efficiently tackle large-scale real-world problems that were deemed intractable just a few decades ago. However, provably optimal solutions may not be accepted due to the perception of optimization software as a black box. Although well understood by scientists, this lacks easy accessibility for practitioners. Hence, we advocate for introducing the explainability of a solution as another evaluation criterion, next to its objective value, which enables us to find trade-off solutions between these two criteria. Explainability is attained by comparing against (not necessarily optimal) solutions that were implemented in similar situations in the past. Thus, solutions are preferred that exhibit similar features. Although we prove that already in simple cases the explainable model is NP-hard, we characterize relevant polynomially solvable cases such as the explainable shortest-path problem. Our numerical experiments on both artificial as well as real-world road networks show the resulting Pareto front. It turns out that the cost of enforcing explainability can be very small.

A Framework for Inherently Interpretable Optimization Models

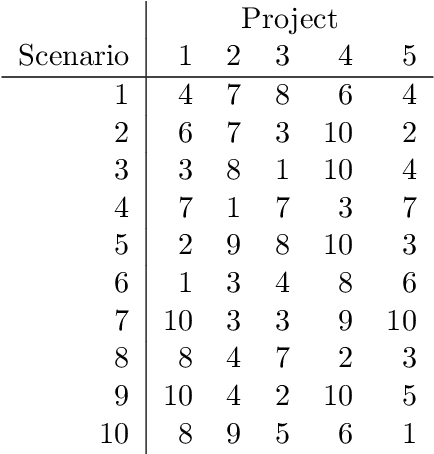
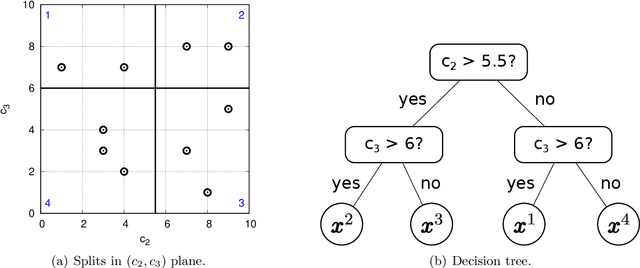
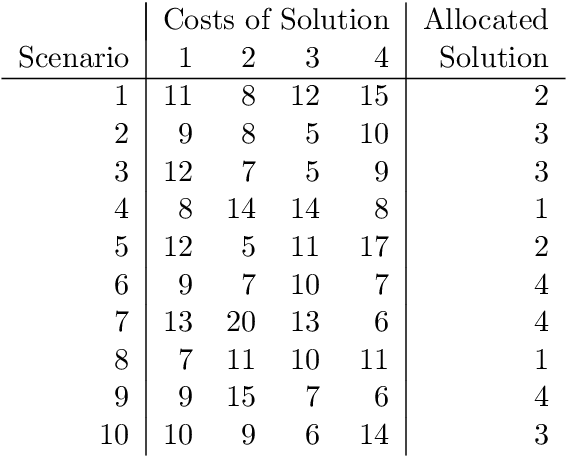
With dramatic improvements in optimization software, the solution of large-scale problems that seemed intractable decades ago are now a routine task. This puts even more real-world applications into the reach of optimizers. At the same time, solving optimization problems often turns out to be one of the smaller difficulties when putting solutions into practice. One major barrier is that the optimization software can be perceived as a black box, which may produce solutions of high quality, but can create completely different solutions when circumstances change leading to low acceptance of optimized solutions. Such issues of interpretability and explainability have seen significant attention in other areas, such as machine learning, but less so in optimization. In this paper we propose an optimization framework to derive solutions that inherently come with an easily comprehensible explanatory rule, under which circumstances which solution should be chosen. Focussing on decision trees to represent explanatory rules, we propose integer programming formulations as well as a heuristic method that ensure applicability of our approach even for large-scale problems. Computational experiments using random and real-world data indicate that the costs of inherent interpretability can be very small.

Data-driven Prediction of Relevant Scenarios for Robust Optimization

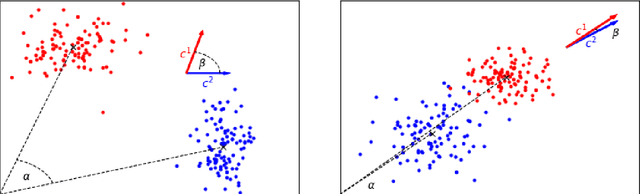
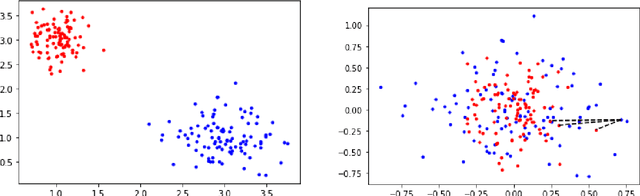
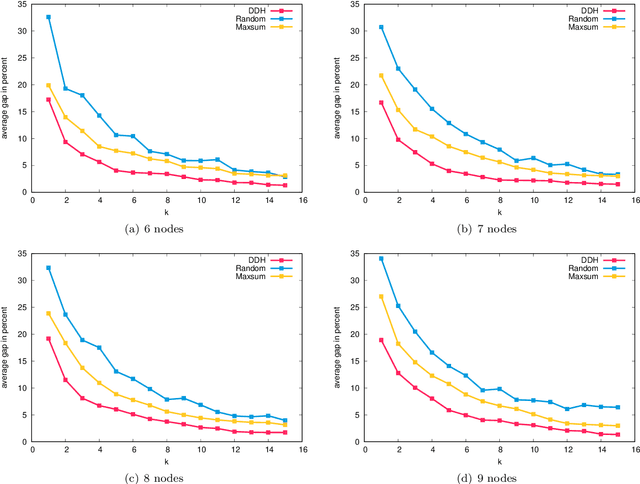
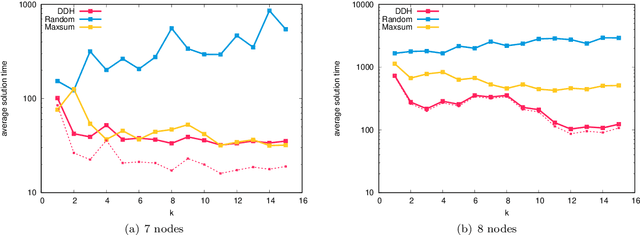
In this work we study robust one- and two-stage problems with discrete uncertainty sets which are known to be hard to solve even if the underlying deterministic problem is easy. Popular solution methods iteratively generate scenario constraints and possibly second-stage variables. This way, by solving a sequence of smaller problems, it is often possible to avoid the complexity of considering all scenarios simultaneously. A key ingredient for the performance of the iterative methods is a good selection of start scenarios. In this paper we propose a data-driven heuristic to seed the iterative solution method with a set of starting scenarios that provide a strong lower bound early in the process, and result in considerably smaller overall solution times compared to other benchmark methods. Our heuristic learns the relevance of a scenario by extracting information from training data based on a combined similarity measure between robust problem instances and single scenarios. Our experiments show that predicting even a small number of good start scenarios by our method can considerably reduce the computation time of the iterative methods.

Data-Driven Robust Optimization using Unsupervised Deep Learning

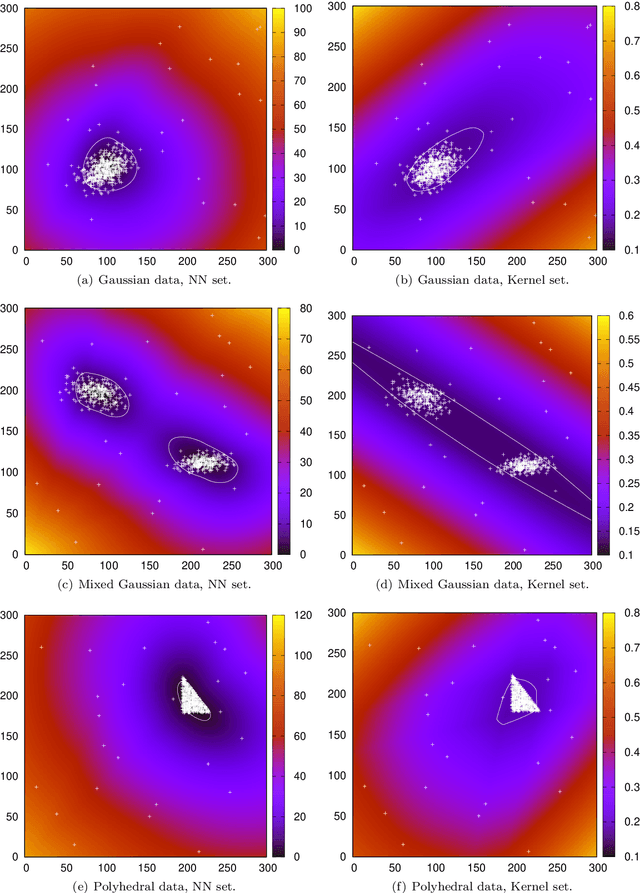
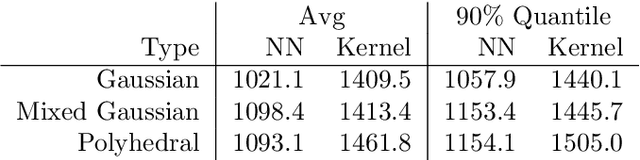
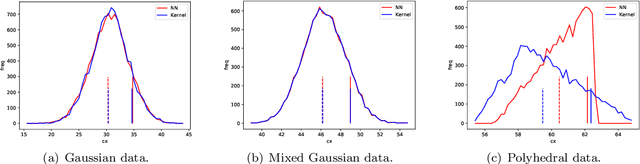
Robust optimization has been established as a leading methodology to approach decision problems under uncertainty. To derive a robust optimization model, a central ingredient is to identify a suitable model for uncertainty, which is called the uncertainty set, containing all scenarios against which we wish to protect. An ongoing challenge in the recent literature is to derive uncertainty sets from given historical data. In this paper we use an unsupervised deep learning method to construct non-convex uncertainty sets from data, which have a more complex structure than the typically considered sets. We show that the trained neural networks can be integrated into a robust optimization model by formulating the adversarial problem as a convex quadratic mixed-integer program. This allows us to derive robust solutions through an iterative scenario generation process. In extensive computational experiments, we compare this approach to a current state-of-the-art approach, which derives uncertainty sets by kernel-based support vector clustering. We find that uncertainty sets derived by the unsupervised deep learning method can give a better description of data, leading to robust solutions that considerably outperform the comparison method both with respect to objective value and feasibility.

Automatic Generation of Algorithms for Black-Box Robust Optimisation Problems

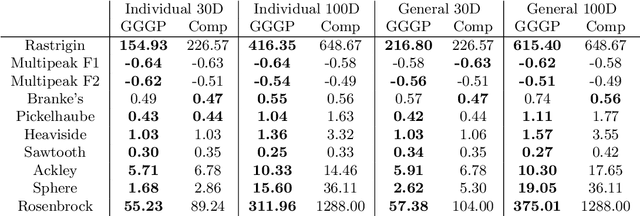
We develop algorithms capable of tackling robust black-box optimisation problems, where the number of model runs is limited. When a desired solution cannot be implemented exactly the aim is to find a robust one, where the worst case in an uncertainty neighbourhood around a solution still performs well. This requires a local maximisation within a global minimisation. To investigate improved optimisation methods for robust problems, and remove the need to manually determine an effective heuristic and parameter settings, we employ an automatic generation of algorithms approach: Grammar-Guided Genetic Programming. We develop algorithmic building blocks to be implemented in a Particle Swarm Optimisation framework, define the rules for constructing heuristics from these components, and evolve populations of search algorithms. Our algorithmic building blocks combine elements of existing techniques and new features, resulting in the investigation of a novel heuristic solution space. As a result of this evolutionary process we obtain algorithms which improve upon the current state of the art. We also analyse the component level breakdowns of the populations of algorithms developed against their performance, to identify high-performing heuristic components for robust problems.

Mixed Uncertainty Sets for Robust Combinatorial Optimization

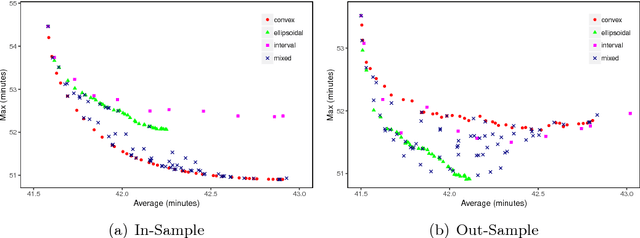
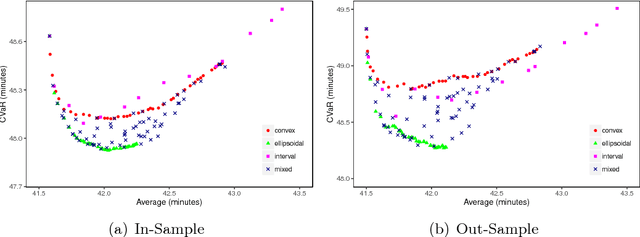
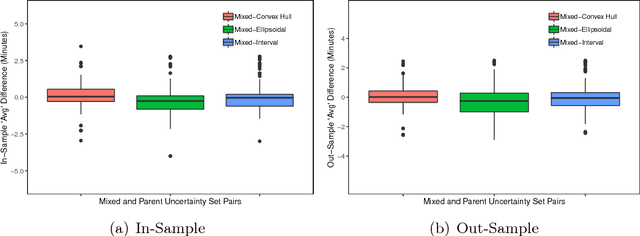
In robust optimization, the uncertainty set is used to model all possible outcomes of uncertain parameters. In the classic setting, one assumes that this set is provided by the decision maker based on the data available to her. Only recently it has been recognized that the process of building useful uncertainty sets is in itself a challenging task that requires mathematical support. In this paper, we propose an approach to go beyond the classic setting, by assuming multiple uncertainty sets to be prepared, each with a weight showing the degree of belief that the set is a "true" model of uncertainty. We consider theoretical aspects of this approach and show that it is as easy to model as the classic setting. In an extensive computational study using a shortest path problem based on real-world data, we auto-tune uncertainty sets to the available data, and show that with regard to out-sample performance, the combination of multiple sets can give better results than each set on its own.