Data-Driven Robust Optimization using Unsupervised Deep Learning
Paper and Code
Nov 19, 2020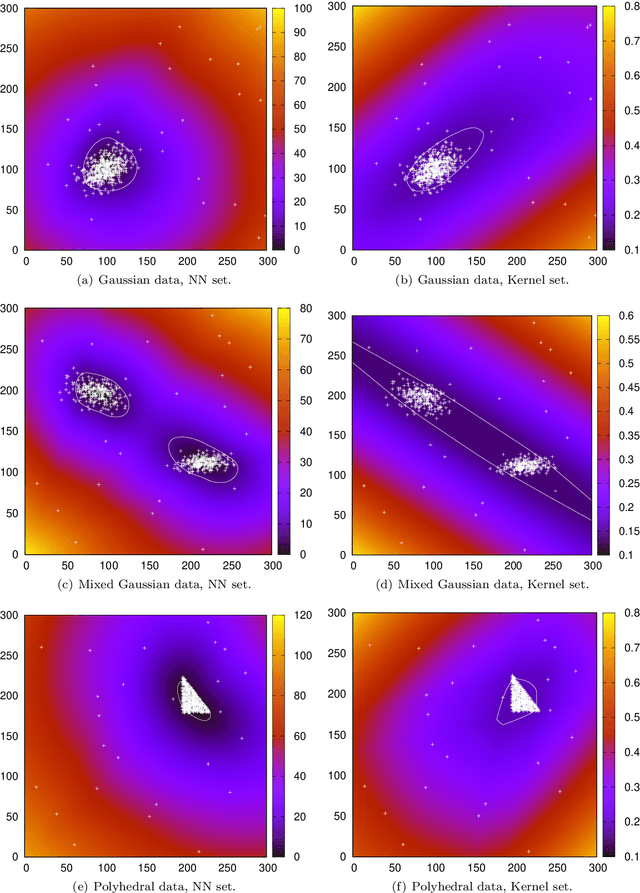
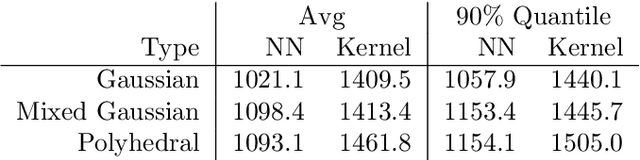
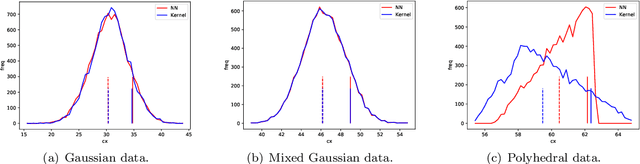

Robust optimization has been established as a leading methodology to approach decision problems under uncertainty. To derive a robust optimization model, a central ingredient is to identify a suitable model for uncertainty, which is called the uncertainty set, containing all scenarios against which we wish to protect. An ongoing challenge in the recent literature is to derive uncertainty sets from given historical data. In this paper we use an unsupervised deep learning method to construct non-convex uncertainty sets from data, which have a more complex structure than the typically considered sets. We show that the trained neural networks can be integrated into a robust optimization model by formulating the adversarial problem as a convex quadratic mixed-integer program. This allows us to derive robust solutions through an iterative scenario generation process. In extensive computational experiments, we compare this approach to a current state-of-the-art approach, which derives uncertainty sets by kernel-based support vector clustering. We find that uncertainty sets derived by the unsupervised deep learning method can give a better description of data, leading to robust solutions that considerably outperform the comparison method both with respect to objective value and feasibility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge