Automatic Generation of Algorithms for Black-Box Robust Optimisation Problems

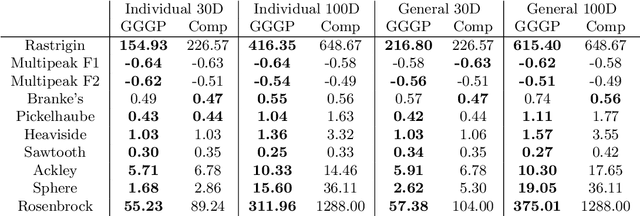
We develop algorithms capable of tackling robust black-box optimisation problems, where the number of model runs is limited. When a desired solution cannot be implemented exactly the aim is to find a robust one, where the worst case in an uncertainty neighbourhood around a solution still performs well. This requires a local maximisation within a global minimisation. To investigate improved optimisation methods for robust problems, and remove the need to manually determine an effective heuristic and parameter settings, we employ an automatic generation of algorithms approach: Grammar-Guided Genetic Programming. We develop algorithmic building blocks to be implemented in a Particle Swarm Optimisation framework, define the rules for constructing heuristics from these components, and evolve populations of search algorithms. Our algorithmic building blocks combine elements of existing techniques and new features, resulting in the investigation of a novel heuristic solution space. As a result of this evolutionary process we obtain algorithms which improve upon the current state of the art. We also analyse the component level breakdowns of the populations of algorithms developed against their performance, to identify high-performing heuristic components for robust problems.

Approximate policy iteration using neural networks for storage problems

We consider the stochastic single node energy storage problem (SNES) and revisit Approximate Policy Iteration (API) to solve SNES. We show that the performance of API can be boosted by using neural networks as an approximation architecture at the policy evaluation stage. To achieve this, we use a model different to that in literature with aggregate variables reducing the dimensionality of the decision vector, which in turn makes it viable to use neural network predictions in the policy improvement stage. We show that performance improvement by neural networks is even more significant in the case when charging efficiency of storage systems is low.

Mixed Uncertainty Sets for Robust Combinatorial Optimization

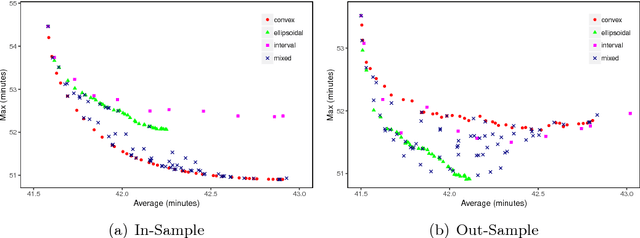
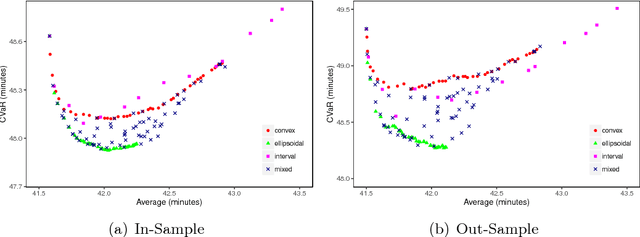
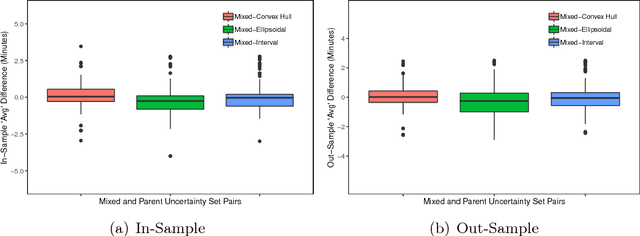
In robust optimization, the uncertainty set is used to model all possible outcomes of uncertain parameters. In the classic setting, one assumes that this set is provided by the decision maker based on the data available to her. Only recently it has been recognized that the process of building useful uncertainty sets is in itself a challenging task that requires mathematical support. In this paper, we propose an approach to go beyond the classic setting, by assuming multiple uncertainty sets to be prepared, each with a weight showing the degree of belief that the set is a "true" model of uncertainty. We consider theoretical aspects of this approach and show that it is as easy to model as the classic setting. In an extensive computational study using a shortest path problem based on real-world data, we auto-tune uncertainty sets to the available data, and show that with regard to out-sample performance, the combination of multiple sets can give better results than each set on its own.