Merlin-Arthur Classifiers: Formal Interpretability with Interactive Black Boxes
Paper and Code
Jun 01, 2022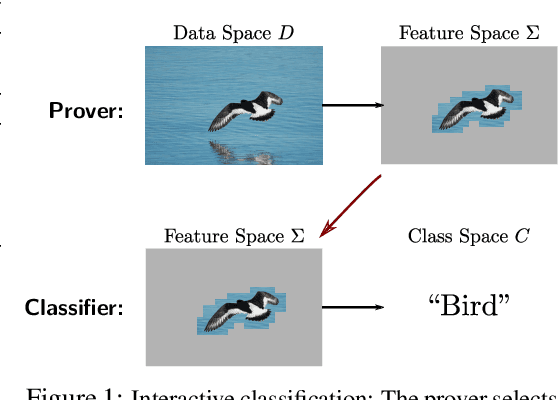

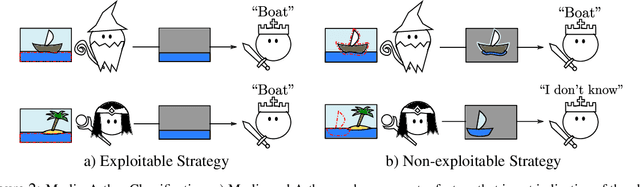

We present a new theoretical framework for making black box classifiers such as Neural Networks interpretable, basing our work on clear assumptions and guarantees. In our setting, which is inspired by the Merlin-Arthur protocol from Interactive Proof Systems, two functions cooperate to achieve a classification together: the \emph{prover} selects a small set of features as a certificate and presents it to the \emph{classifier}. Including a second, adversarial prover allows us to connect a game-theoretic equilibrium to information-theoretic guarantees on the exchanged features. We define notions of completeness and soundness that enable us to lower bound the mutual information between features and class. To demonstrate good agreement between theory and practice, we support our framework by providing numerical experiments for Neural Network classifiers, explicitly calculating the mutual information of features with respect to the class.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge