A Rate-Distortion Framework for Explaining Neural Network Decisions
Paper and Code
May 27, 2019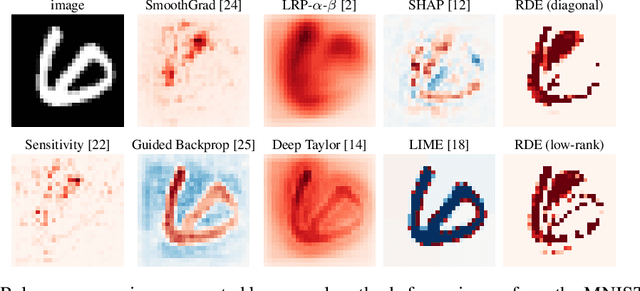
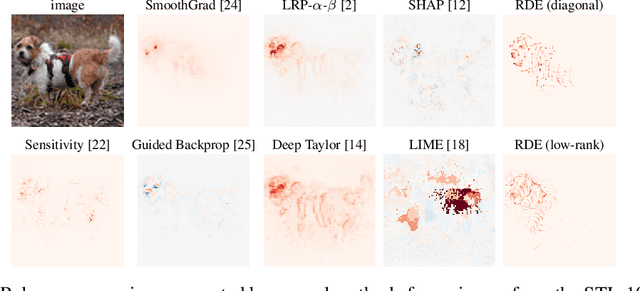
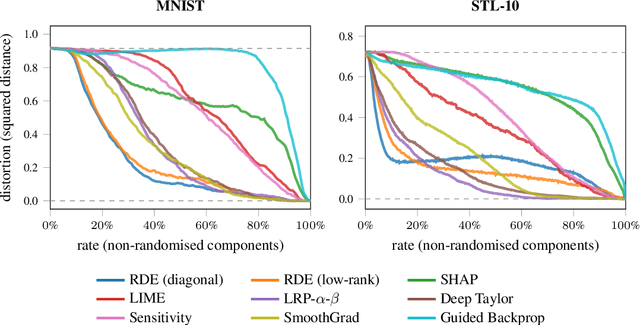
We formalise the widespread idea of interpreting neural network decisions as an explicit optimisation problem in a rate-distortion framework. A set of input features is deemed relevant for a classification decision if the expected classifier score remains nearly constant when randomising the remaining features. We discuss the computational complexity of finding small sets of relevant features and show that the problem is complete for $\mathsf{NP}^\mathsf{PP}$, an important class of computational problems frequently arising in AI tasks. Furthermore, we show that it even remains $\mathsf{NP}$-hard to only approximate the optimal solution to within any non-trivial approximation factor. Finally, we consider a continuous problem relaxation and develop a heuristic solution strategy based on assumed density filtering for deep ReLU neural networks. We present numerical experiments for two image classification data sets where we outperform established methods in particular for sparse explanations of neural network decisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge