Aleph-Alpha-GermanWeb: Improving German-language LLM pre-training with model-based data curation and synthetic data generation

Scaling data quantity is essential for large language models (LLMs), yet recent findings show that data quality can significantly boost performance and training efficiency. We introduce a German-language dataset curation pipeline that combines heuristic and model-based filtering techniques with synthetic data generation. We use our pipeline to create Aleph-Alpha-GermanWeb, a large-scale German pre-training dataset which draws from: (1) Common Crawl web data, (2) FineWeb2, and (3) synthetically-generated data conditioned on actual, organic web data. We evaluate our dataset by pre-training both a 1B Llama-style model and an 8B tokenizer-free hierarchical autoregressive transformer (HAT). A comparison on German-language benchmarks, including MMMLU, shows significant performance gains of Aleph-Alpha-GermanWeb over FineWeb2 alone. This advantage holds at the 8B scale even when FineWeb2 is enriched by human-curated high-quality data sources such as Wikipedia. Our findings support the growing body of evidence that model-based data curation and synthetic data generation can significantly enhance LLM pre-training datasets.

Associative memory inspires improvements for in-context learning using a novel attention residual stream architecture

Large language models (LLMs) demonstrate an impressive ability to utilise information within the context of their input sequences to appropriately respond to data unseen by the LLM during its training procedure. This ability is known as in-context learning (ICL). Humans and non-human animals demonstrate similar abilities, however their neural architectures differ substantially from LLMs. Despite this, a critical component within LLMs, the attention mechanism, resembles modern associative memory models, widely used in and influenced by the computational neuroscience community to model biological memory systems. Using this connection, we introduce an associative memory model capable of performing ICL. We use this as inspiration for a novel residual stream architecture which allows information to directly flow between attention heads. We test this architecture during training within a two-layer Transformer and show its ICL abilities manifest more quickly than without this modification. We then apply our architecture in small language models with 8 million parameters, focusing on attention head values, with results also indicating improved ICL performance at this larger and more naturalistic scale.

Semantically-correlated memories in a dense associative model

I introduce a novel associative memory model named Correlated Dense Associative Memory (CDAM), which integrates both auto- and hetero-association in a unified framework for continuous-valued memory patterns. Employing an arbitrary graph structure to semantically link memory patterns, CDAM is theoretically and numerically analysed, revealing four distinct dynamical modes: auto-association, narrow hetero-association, wide hetero-association, and neutral quiescence. Drawing inspiration from inhibitory modulation studies, I employ anti-Hebbian learning rules to control the range of hetero-association, extract multi-scale representations of community structures in graphs, and stabilise the recall of temporal sequences. Experimental demonstrations showcase CDAM's efficacy in handling real-world data, replicating a classical neuroscience experiment, performing image retrieval, and simulating arbitrary finite automata.

Simplicial Hopfield networks

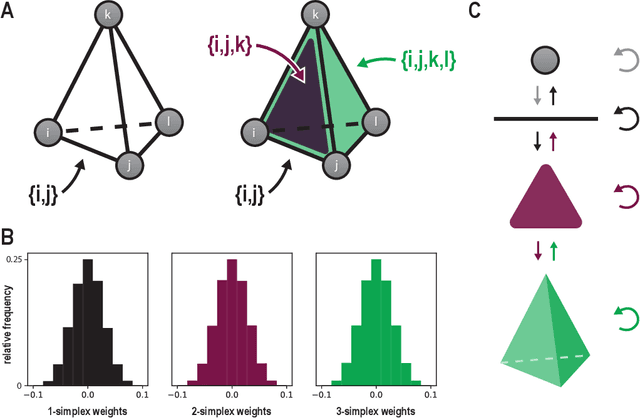
Hopfield networks are artificial neural networks which store memory patterns on the states of their neurons by choosing recurrent connection weights and update rules such that the energy landscape of the network forms attractors around the memories. How many stable, sufficiently-attracting memory patterns can we store in such a network using $N$ neurons? The answer depends on the choice of weights and update rule. Inspired by setwise connectivity in biology, we extend Hopfield networks by adding setwise connections and embedding these connections in a simplicial complex. Simplicial complexes are higher dimensional analogues of graphs which naturally represent collections of pairwise and setwise relationships. We show that our simplicial Hopfield networks increase memory storage capacity. Surprisingly, even when connections are limited to a small random subset of equivalent size to an all-pairwise network, our networks still outperform their pairwise counterparts. Such scenarios include non-trivial simplicial topology. We also test analogous modern continuous Hopfield networks, offering a potentially promising avenue for improving the attention mechanism in Transformer models.

Efficient, probabilistic analysis of combinatorial neural codes

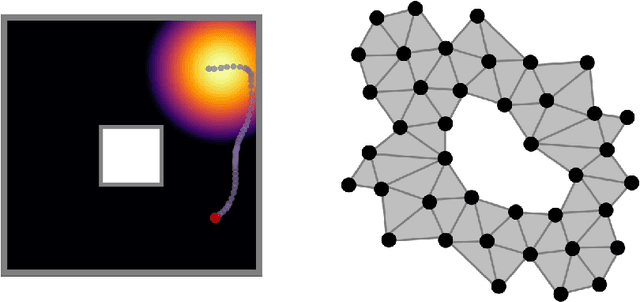
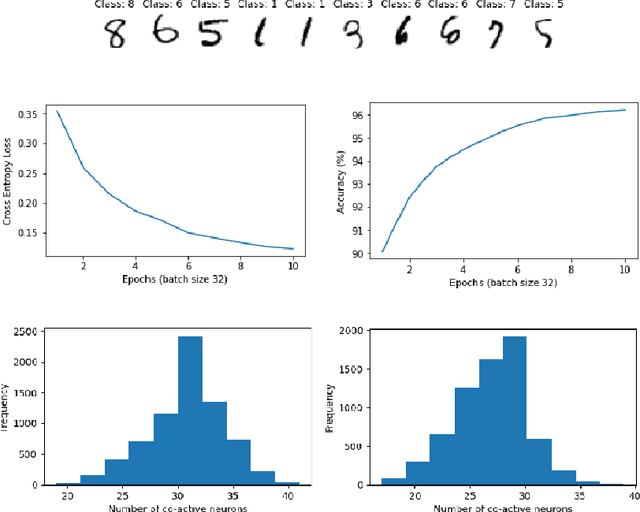
Artificial and biological neural networks (ANNs and BNNs) can encode inputs in the form of combinations of individual neurons' activities. These combinatorial neural codes present a computational challenge for direct and efficient analysis due to their high dimensionality and often large volumes of data. Here we improve the computational complexity -- from factorial to quadratic time -- of direct algebraic methods previously applied to small examples and apply them to large neural codes generated by experiments. These methods provide a novel and efficient way of probing algebraic, geometric, and topological characteristics of combinatorial neural codes and provide insights into how such characteristics are related to learning and experience in neural networks. We introduce a procedure to perform hypothesis testing on the intrinsic features of neural codes using information geometry. We then apply these methods to neural activities from an ANN for image classification and a BNN for 2D navigation to, without observing any inputs or outputs, estimate the structure and dimensionality of the stimulus or task space. Additionally, we demonstrate how an ANN varies its internal representations across network depth and during learning.

Detecting danger in gridworlds using Gromov's Link Condition

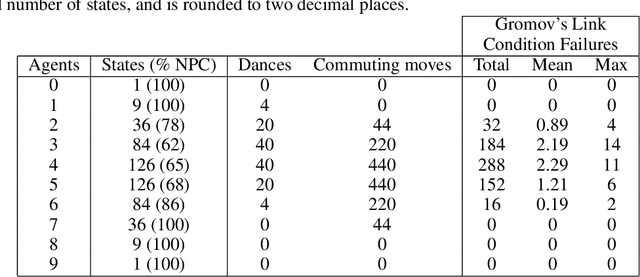
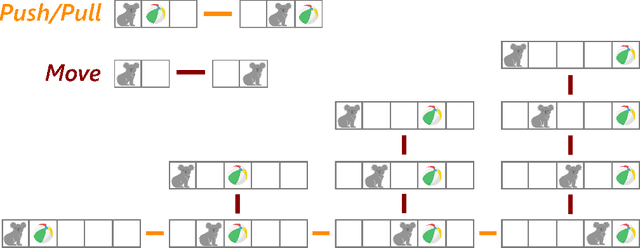
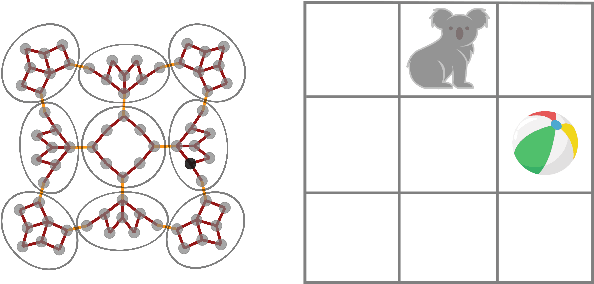
Gridworlds have been long-utilised in AI research, particularly in reinforcement learning, as they provide simple yet scalable models for many real-world applications such as robot navigation, emergent behaviour, and operations research. We initiate a study of gridworlds using the mathematical framework of reconfigurable systems and state complexes due to Abrams, Ghrist & Peterson. State complexes represent all possible configurations of a system as a single geometric space, thus making them conducive to study using geometric, topological, or combinatorial methods. The main contribution of this work is a modification to the original Abrams, Ghrist & Peterson setup which we believe is more naturally-suited to the context of gridworlds. With this modification, the state complexes may exhibit geometric defects (failure of Gromov's Link Condition), however, we argue that these failures can indicate undesirable or dangerous states in the gridworld. Our results provide a novel method for seeking guaranteed safety limitations in discrete task environments with single or multiple agents, and offer potentially useful geometric and topological information for incorporation in or analysis of machine learning systems.