Robert Tang
Detecting danger in gridworlds using Gromov's Link Condition
Jan 17, 2022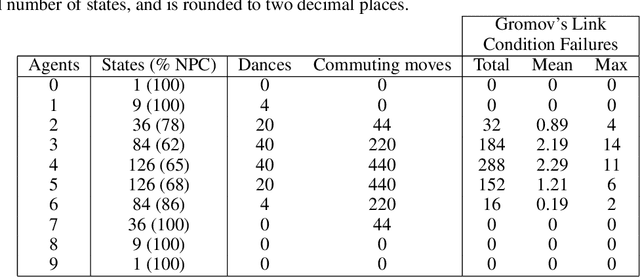
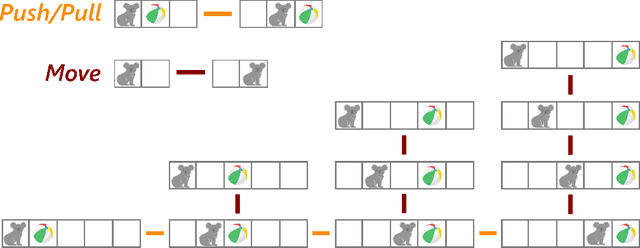

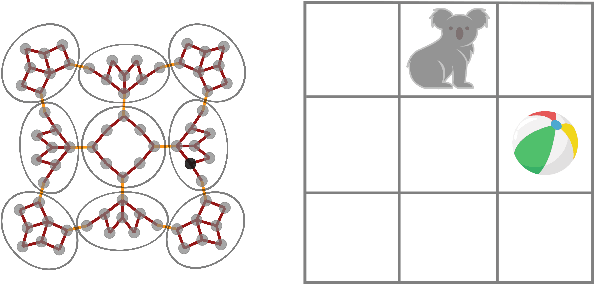
Abstract:Gridworlds have been long-utilised in AI research, particularly in reinforcement learning, as they provide simple yet scalable models for many real-world applications such as robot navigation, emergent behaviour, and operations research. We initiate a study of gridworlds using the mathematical framework of reconfigurable systems and state complexes due to Abrams, Ghrist & Peterson. State complexes represent all possible configurations of a system as a single geometric space, thus making them conducive to study using geometric, topological, or combinatorial methods. The main contribution of this work is a modification to the original Abrams, Ghrist & Peterson setup which we believe is more naturally-suited to the context of gridworlds. With this modification, the state complexes may exhibit geometric defects (failure of Gromov's Link Condition), however, we argue that these failures can indicate undesirable or dangerous states in the gridworld. Our results provide a novel method for seeking guaranteed safety limitations in discrete task environments with single or multiple agents, and offer potentially useful geometric and topological information for incorporation in or analysis of machine learning systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge