Solving the Tree Containment Problem Using Graph Neural Networks

Tree Containment is a fundamental problem in phylogenetics useful for verifying a proposed phylogenetic network, representing the evolutionary history of certain species. Tree Containment asks whether the given phylogenetic tree (for instance, constructed from a DNA fragment showing tree-like evolution) is contained in the given phylogenetic network. In the general case, this is an NP-complete problem. We propose to solve it approximately using Graph Neural Networks. In particular, we propose to combine the given network and the tree and apply a Graph Neural Network to this network-tree graph. This way, we achieve the capability of solving the tree containment instances representing a larger number of species than the instances contained in the training dataset (i.e., our algorithm has the inductive learning ability). Our algorithm demonstrates an accuracy of over $95\%$ in solving the tree containment problem on instances with up to 100 leaves.

Neur2BiLO: Neural Bilevel Optimization

Bilevel optimization deals with nested problems in which a leader takes the first decision to minimize their objective function while accounting for a follower's best-response reaction. Constrained bilevel problems with integer variables are particularly notorious for their hardness. While exact solvers have been proposed for mixed-integer linear bilevel optimization, they tend to scale poorly with problem size and are hard to generalize to the non-linear case. On the other hand, problem-specific algorithms (exact and heuristic) are limited in scope. Under a data-driven setting in which similar instances of a bilevel problem are solved routinely, our proposed framework, Neur2BiLO, embeds a neural network approximation of the leader's or follower's value function, trained via supervised regression, into an easy-to-solve mixed-integer program. Neur2BiLO serves as a heuristic that produces high-quality solutions extremely fast for the bilevel knapsack interdiction problem, the "critical node game" from network security, a donor-recipient healthcare problem, and discrete network design from transportation planning. These problems are diverse in that they have linear or non-linear objectives/constraints and integer or mixed-integer variables, making Neur2BiLO unique in its versatility.

Neur2RO: Neural Two-Stage Robust Optimization

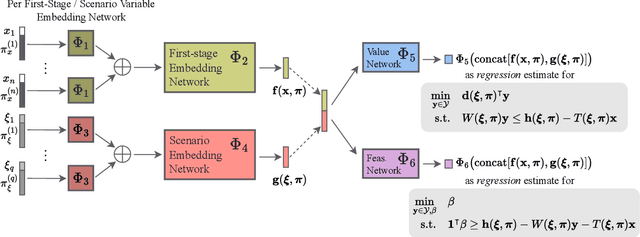
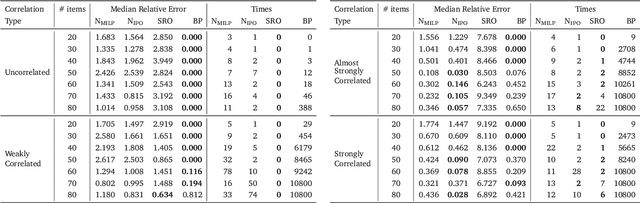
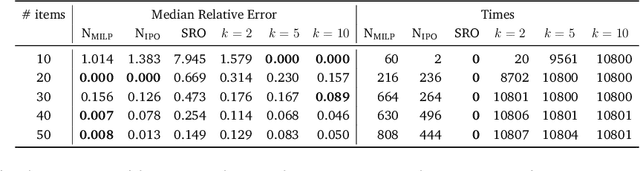
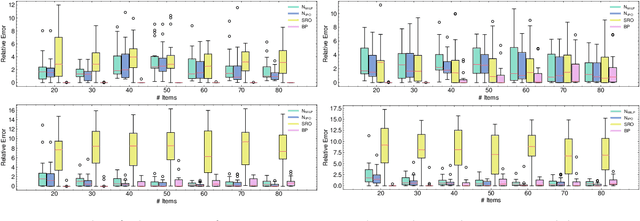
Robust optimization provides a mathematical framework for modeling and solving decision-making problems under worst-case uncertainty. This work addresses two-stage robust optimization (2RO) problems (also called adjustable robust optimization), wherein first-stage and second-stage decisions are made before and after uncertainty is realized, respectively. This results in a nested min-max-min optimization problem which is extremely challenging computationally, especially when the decisions are discrete. We propose Neur2RO, an efficient machine learning-driven instantiation of column-and-constraint generation (CCG), a classical iterative algorithm for 2RO. Specifically, we learn to estimate the value function of the second-stage problem via a novel neural network architecture that is easy to optimize over by design. Embedding our neural network into CCG yields high-quality solutions quickly as evidenced by experiments on two 2RO benchmarks, knapsack and capital budgeting. For knapsack, Neur2RO finds solutions that are within roughly $2\%$ of the best-known values in a few seconds compared to the three hours of the state-of-the-art exact branch-and-price algorithm; for larger and more complex instances, Neur2RO finds even better solutions. For capital budgeting, Neur2RO outperforms three variants of the $k$-adaptability algorithm, particularly on the largest instances, with a 5 to 10-fold reduction in solution time. Our code and data are available at https://github.com/khalil-research/Neur2RO.

Constructing Phylogenetic Networks via Cherry Picking and Machine Learning

Combining a set of phylogenetic trees into a single phylogenetic network that explains all of them is a fundamental challenge in evolutionary studies. Existing methods are computationally expensive and can either handle only small numbers of phylogenetic trees or are limited to severely restricted classes of networks. In this paper, we apply the recently-introduced theoretical framework of cherry picking to design a class of efficient heuristics that are guaranteed to produce a network containing each of the input trees, for datasets consisting of binary trees. Some of the heuristics in this framework are based on the design and training of a machine learning model that captures essential information on the structure of the input trees and guides the algorithms towards better solutions. We also propose simple and fast randomised heuristics that prove to be very effective when run multiple times. Unlike the existing exact methods, our heuristics are applicable to datasets of practical size, and the experimental study we conducted on both simulated and real data shows that these solutions are qualitatively good, always within some small constant factor from the optimum. Moreover, our machine-learned heuristics are one of the first applications of machine learning to phylogenetics and show its promise.