Learn2Aggregate: Supervised Generation of Chvátal-Gomory Cuts Using Graph Neural Networks

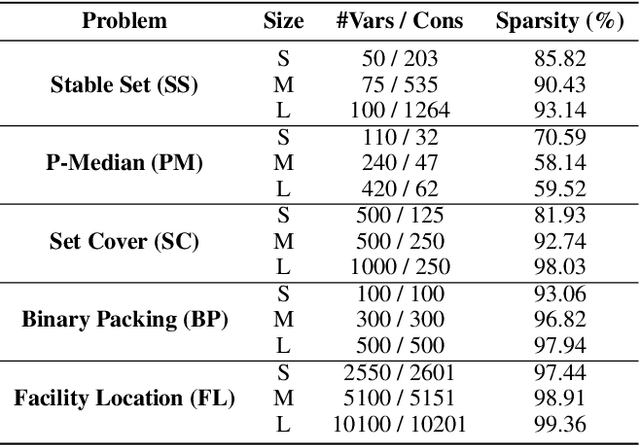
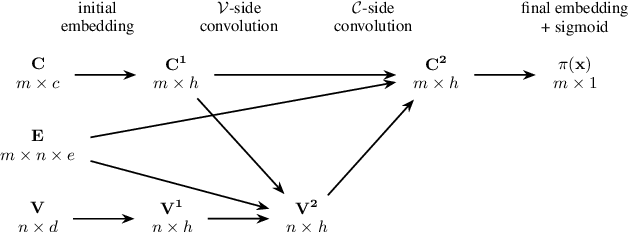
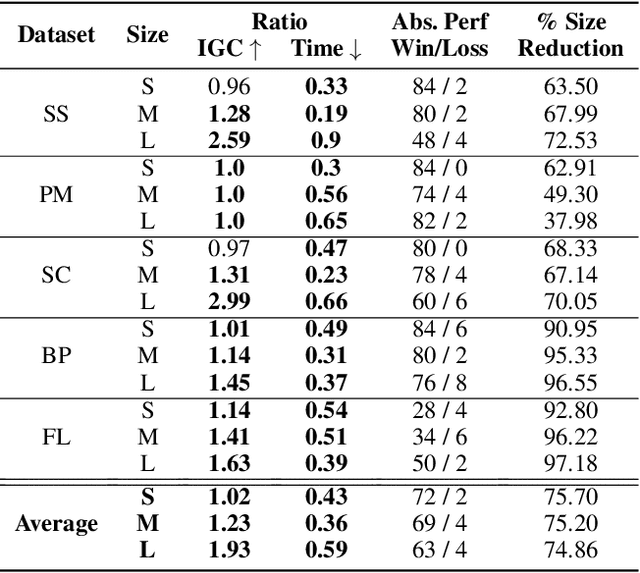
We present $\textit{Learn2Aggregate}$, a machine learning (ML) framework for optimizing the generation of Chv\'atal-Gomory (CG) cuts in mixed integer linear programming (MILP). The framework trains a graph neural network to classify useful constraints for aggregation in CG cut generation. The ML-driven CG separator selectively focuses on a small set of impactful constraints, improving runtimes without compromising the strength of the generated cuts. Key to our approach is the formulation of a constraint classification task which favours sparse aggregation of constraints, consistent with empirical findings. This, in conjunction with a careful constraint labeling scheme and a hybrid of deep learning and feature engineering, results in enhanced CG cut generation across five diverse MILP benchmarks. On the largest test sets, our method closes roughly $\textit{twice}$ as much of the integrality gap as the standard CG method while running 40$% faster. This performance improvement is due to our method eliminating 75% of the constraints prior to aggregation.

Fast Matrix Multiplication Without Tears: A Constraint Programming Approach

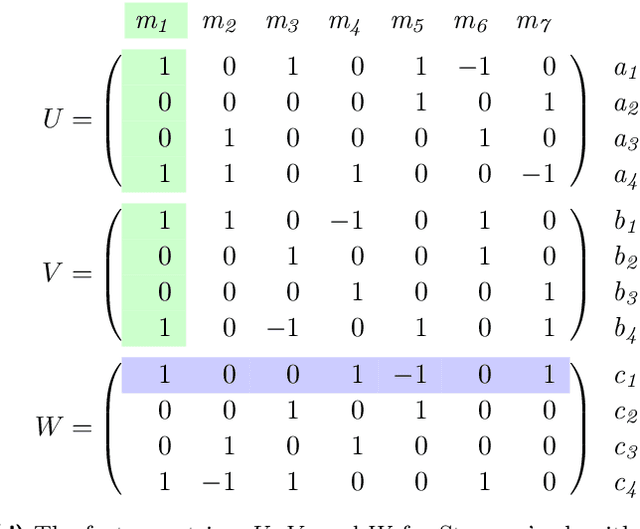
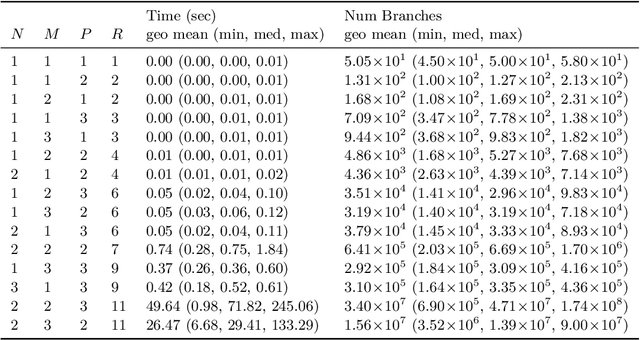
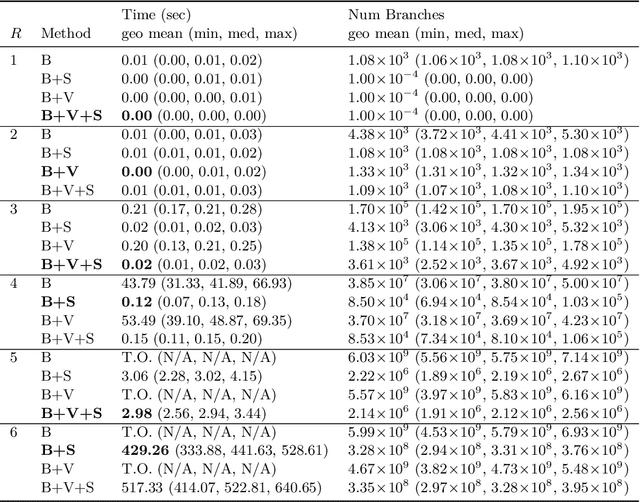
It is known that the multiplication of an $N \times M$ matrix with an $M \times P$ matrix can be performed using fewer multiplications than what the naive $NMP$ approach suggests. The most famous instance of this is Strassen's algorithm for multiplying two $2\times 2$ matrices in 7 instead of 8 multiplications. This gives rise to the constraint satisfaction problem of fast matrix multiplication, where a set of $R < NMP$ multiplication terms must be chosen and combined such that they satisfy correctness constraints on the output matrix. Despite its highly combinatorial nature, this problem has not been exhaustively examined from that perspective, as evidenced for example by the recent deep reinforcement learning approach of AlphaTensor. In this work, we propose a simple yet novel Constraint Programming approach to find non-commutative algorithms for fast matrix multiplication or provide proof of infeasibility otherwise. We propose a set of symmetry-breaking constraints and valid inequalities that are particularly helpful in proving infeasibility. On the feasible side, we find that exploiting solver performance variability in conjunction with a sparsity-based problem decomposition enables finding solutions for larger (feasible) instances of fast matrix multiplication. Our experimental results using CP Optimizer demonstrate that we can find fast matrix multiplication algorithms for matrices up to $3\times 3$ in a short amount of time.

Machine Learning for Cutting Planes in Integer Programming: A Survey

We survey recent work on machine learning (ML) techniques for selecting cutting planes (or cuts) in mixed-integer linear programming (MILP). Despite the availability of various classes of cuts, the task of choosing a set of cuts to add to the linear programming (LP) relaxation at a given node of the branch-and-bound (B&B) tree has defied both formal and heuristic solutions to date. ML offers a promising approach for improving the cut selection process by using data to identify promising cuts that accelerate the solution of MILP instances. This paper presents an overview of the topic, highlighting recent advances in the literature, common approaches to data collection, evaluation, and ML model architectures. We analyze the empirical results in the literature in an attempt to quantify the progress that has been made and conclude by suggesting avenues for future research.