Burning RED: Unlocking Subtask-Driven Reinforcement Learning and Risk-Awareness in Average-Reward Markov Decision Processes

Average-reward Markov decision processes (MDPs) provide a foundational framework for sequential decision-making under uncertainty. However, average-reward MDPs have remained largely unexplored in reinforcement learning (RL) settings, with the majority of RL-based efforts having been allocated to episodic and discounted MDPs. In this work, we study a unique structural property of average-reward MDPs and utilize it to introduce Reward-Extended Differential (or RED) reinforcement learning: a novel RL framework that can be used to effectively and efficiently solve various subtasks simultaneously in the average-reward setting. We introduce a family of RED learning algorithms for prediction and control, including proven-convergent algorithms for the tabular case. We then showcase the power of these algorithms by demonstrating how they can be used to learn a policy that optimizes, for the first time, the well-known conditional value-at-risk (CVaR) risk measure in a fully-online manner, without the use of an explicit bi-level optimization scheme or an augmented state-space.

Bayesian Optimization Framework for Efficient Fleet Design in Autonomous Multi-Robot Exploration

This study addresses the challenge of fleet design optimization in the context of heterogeneous multi-robot fleets, aiming to obtain feasible designs that balance performance and costs. In the domain of autonomous multi-robot exploration, reinforcement learning agents play a central role, offering adaptability to complex terrains and facilitating collaboration among robots. However, modifying the fleet composition results in changes in the learned behavior, and training multi-robot systems using multi-agent reinforcement learning is expensive. Therefore, an exhaustive evaluation of each potential fleet design is infeasible. To tackle these hurdles, we introduce Bayesian Optimization for Fleet Design (BOFD), a framework leveraging multi-objective Bayesian Optimization to explore fleets on the Pareto front of performance and cost while accounting for uncertainty in the design space. Moreover, we establish a sub-linear bound for cumulative regret, supporting BOFD's robustness and efficacy. Extensive benchmark experiments in synthetic and simulated environments demonstrate the superiority of our framework over state-of-the-art methods, achieving efficient fleet designs with minimal fleet evaluations.

Unsupervised Few-shot Learning via Deep Laplacian Eigenmaps

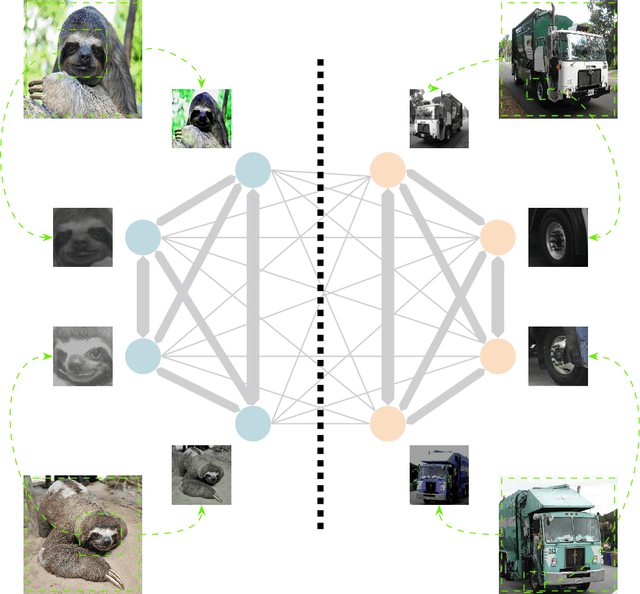
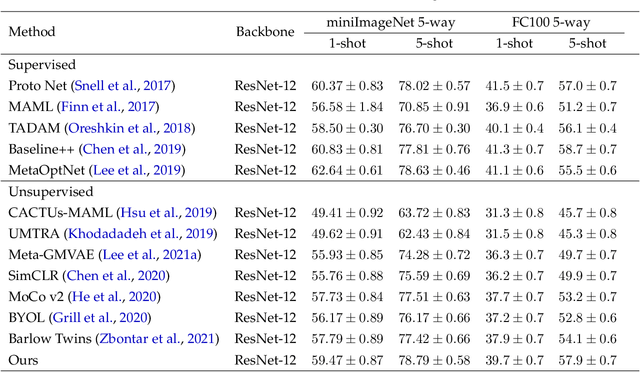
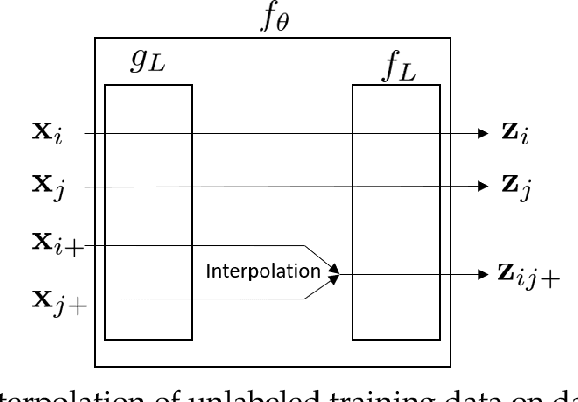
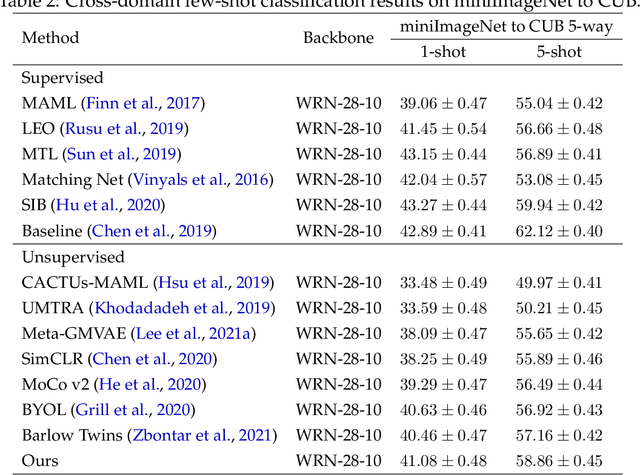
Learning a new task from a handful of examples remains an open challenge in machine learning. Despite the recent progress in few-shot learning, most methods rely on supervised pretraining or meta-learning on labeled meta-training data and cannot be applied to the case where the pretraining data is unlabeled. In this study, we present an unsupervised few-shot learning method via deep Laplacian eigenmaps. Our method learns representation from unlabeled data by grouping similar samples together and can be intuitively interpreted by random walks on augmented training data. We analytically show how deep Laplacian eigenmaps avoid collapsed representation in unsupervised learning without explicit comparison between positive and negative samples. The proposed method significantly closes the performance gap between supervised and unsupervised few-shot learning. Our method also achieves comparable performance to current state-of-the-art self-supervised learning methods under linear evaluation protocol.

Quantum-Inspired Tensor Neural Networks for Partial Differential Equations

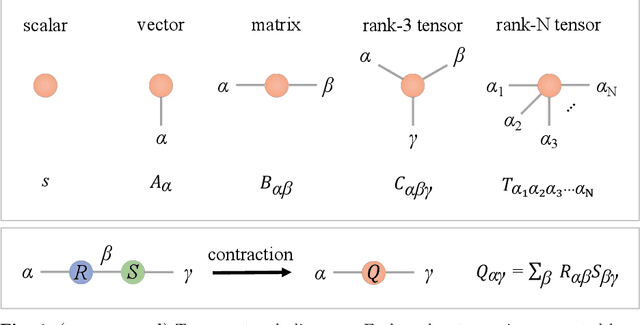
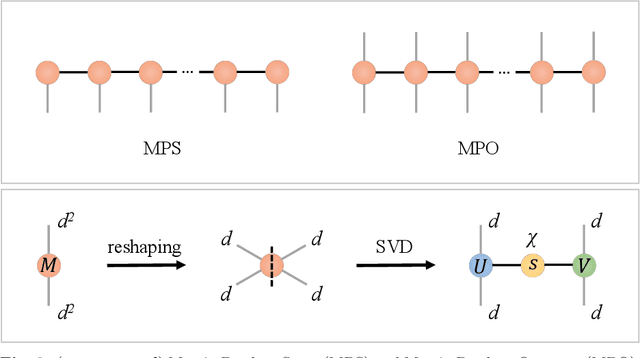
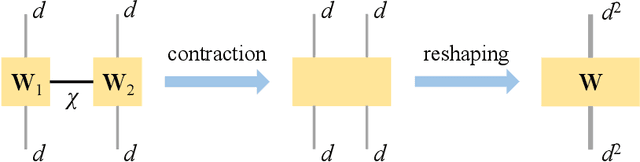
Partial Differential Equations (PDEs) are used to model a variety of dynamical systems in science and engineering. Recent advances in deep learning have enabled us to solve them in a higher dimension by addressing the curse of dimensionality in new ways. However, deep learning methods are constrained by training time and memory. To tackle these shortcomings, we implement Tensor Neural Networks (TNN), a quantum-inspired neural network architecture that leverages Tensor Network ideas to improve upon deep learning approaches. We demonstrate that TNN provide significant parameter savings while attaining the same accuracy as compared to the classical Dense Neural Network (DNN). In addition, we also show how TNN can be trained faster than DNN for the same accuracy. We benchmark TNN by applying them to solve parabolic PDEs, specifically the Black-Scholes-Barenblatt equation, widely used in financial pricing theory, empirically showing the advantages of TNN over DNN. Further examples, such as the Hamilton-Jacobi-Bellman equation, are also discussed.

Don't overfit the history -- Recursive time series data augmentation

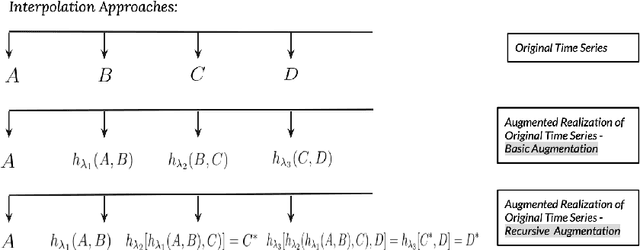
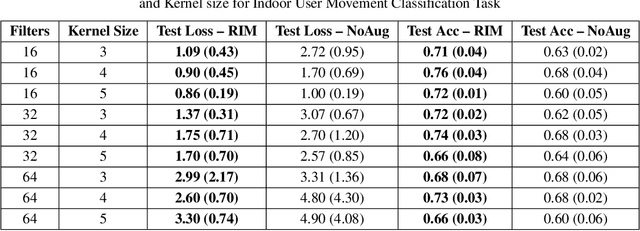
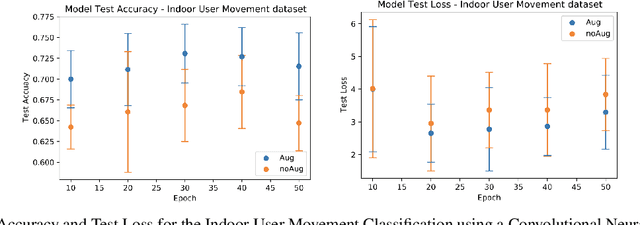
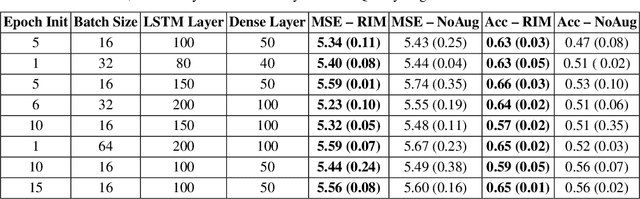
Time series observations can be seen as realizations of an underlying dynamical system governed by rules that we typically do not know. For time series learning tasks, we need to understand that we fit our model on available data, which is a unique realized history. Training on a single realization often induces severe overfitting lacking generalization. To address this issue, we introduce a general recursive framework for time series augmentation, which we call Recursive Interpolation Method, denoted as RIM. New samples are generated using a recursive interpolation function of all previous values in such a way that the enhanced samples preserve the original inherent time series dynamics. We perform theoretical analysis to characterize the proposed RIM and to guarantee its test performance. We apply RIM to diverse real world time series cases to achieve strong performance over non-augmented data on regression, classification, and reinforcement learning tasks.

Meta-free few-shot learning via representation learning with weight averaging

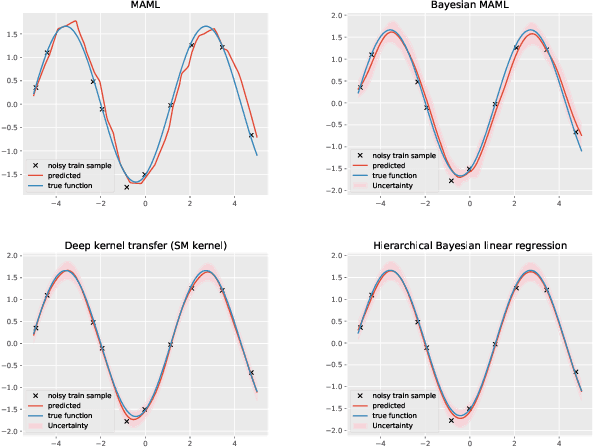
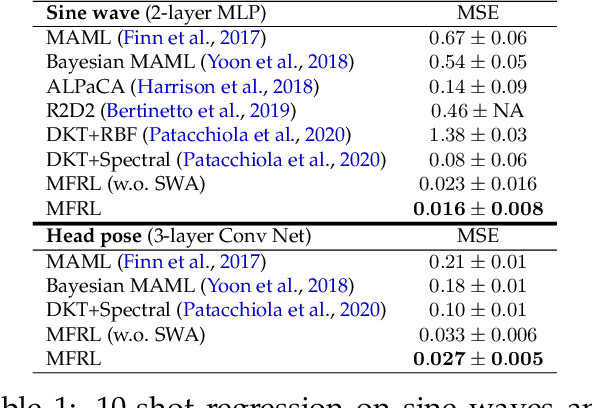
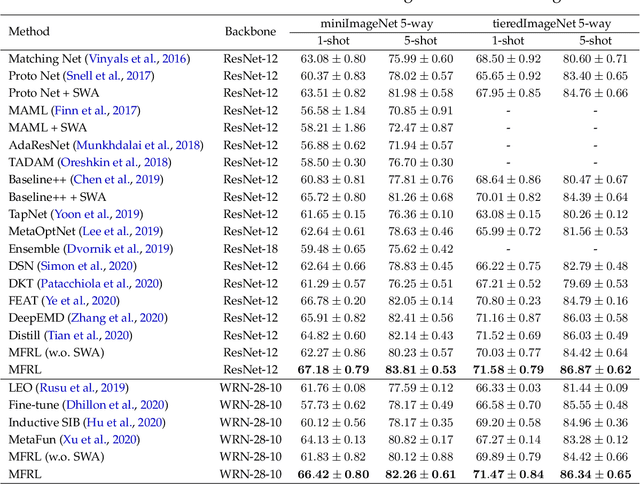
Recent studies on few-shot classification using transfer learning pose challenges to the effectiveness and efficiency of episodic meta-learning algorithms. Transfer learning approaches are a natural alternative, but they are restricted to few-shot classification. Moreover, little attention has been on the development of probabilistic models with well-calibrated uncertainty from few-shot samples, except for some Bayesian episodic learning algorithms. To tackle the aforementioned issues, we propose a new transfer learning method to obtain accurate and reliable models for few-shot regression and classification. The resulting method does not require episodic meta-learning and is called meta-free representation learning (MFRL). MFRL first finds low-rank representation generalizing well on meta-test tasks. Given the learned representation, probabilistic linear models are fine-tuned with few-shot samples to obtain models with well-calibrated uncertainty. The proposed method not only achieves the highest accuracy on a wide range of few-shot learning benchmark datasets but also correctly quantifies the prediction uncertainty. In addition, weight averaging and temperature scaling are effective in improving the accuracy and reliability of few-shot learning in existing meta-learning algorithms with a wide range of learning paradigms and model architectures.

Risk-Aware Transfer in Reinforcement Learning using Successor Features

Sample efficiency and risk-awareness are central to the development of practical reinforcement learning (RL) for complex decision-making. The former can be addressed by transfer learning and the latter by optimizing some utility function of the return. However, the problem of transferring skills in a risk-aware manner is not well-understood. In this paper, we address the problem of risk-aware policy transfer between tasks in a common domain that differ only in their reward functions, in which risk is measured by the variance of reward streams. Our approach begins by extending the idea of generalized policy improvement to maximize entropic utilities, thus extending policy improvement via dynamic programming to sets of policies and levels of risk-aversion. Next, we extend the idea of successor features (SF), a value function representation that decouples the environment dynamics from the rewards, to capture the variance of returns. Our resulting risk-aware successor features (RaSF) integrate seamlessly within the RL framework, inherit the superior task generalization ability of SFs, and incorporate risk-awareness into the decision-making. Experiments on a discrete navigation domain and control of a simulated robotic arm demonstrate the ability of RaSFs to outperform alternative methods including SFs, when taking the risk of the learned policies into account.

Attentive Gaussian processes for probabilistic time-series generation

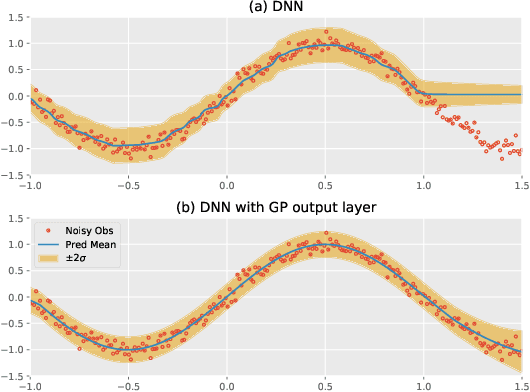
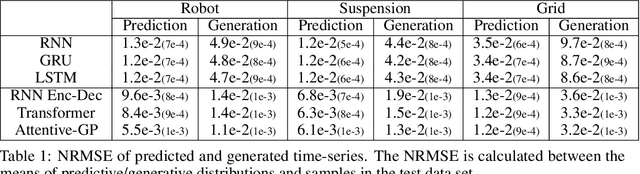
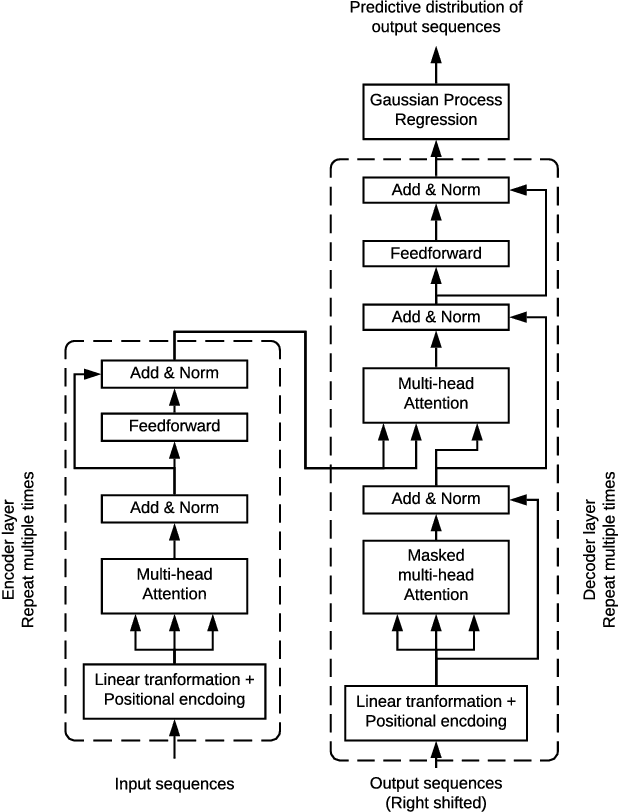
The transduction of sequence has been mostly done by recurrent networks, which are computationally demanding and often underestimate uncertainty severely. We propose a computationally efficient attention-based network combined with the Gaussian process regression to generate real-valued sequence, which we call the Attentive-GP. The proposed model not only improves the training efficiency by dispensing recurrence and convolutions but also learns the factorized generative distribution with Bayesian representation. However, the presence of the GP precludes the commonly used mini-batch approach to the training of the attention network. Therefore, we develop a block-wise training algorithm to allow mini-batch training of the network while the GP is trained using full-batch, resulting in a scalable training method. The algorithm has been proved to converge and shows comparable, if not better, quality of the found solution. As the algorithm does not assume any specific network architecture, it can be used with a wide range of hybrid models such as neural networks with kernel machine layers in the scarcity of resources for computation and memory.

ε-BMC: A Bayesian Ensemble Approach to Epsilon-Greedy Exploration in Model-Free Reinforcement Learning

Resolving the exploration-exploitation trade-off remains a fundamental problem in the design and implementation of reinforcement learning (RL) algorithms. In this paper, we focus on model-free RL using the epsilon-greedy exploration policy, which despite its simplicity, remains one of the most frequently used forms of exploration. However, a key limitation of this policy is the specification of $\varepsilon$. In this paper, we provide a novel Bayesian perspective of $\varepsilon$ as a measure of the uniformity of the Q-value function. We introduce a closed-form Bayesian model update based on Bayesian model combination (BMC), based on this new perspective, which allows us to adapt $\varepsilon$ using experiences from the environment in constant time with monotone convergence guarantees. We demonstrate that our proposed algorithm, $\varepsilon$-\texttt{BMC}, efficiently balances exploration and exploitation on different problems, performing comparably or outperforming the best tuned fixed annealing schedules and an alternative data-dependent $\varepsilon$ adaptation scheme proposed in the literature.

Bayesian Experience Reuse for Learning from Multiple Demonstrators

Learning from demonstrations (LfD) improves the exploration efficiency of a learning agent by incorporating demonstrations from experts. However, demonstration data can often come from multiple experts with conflicting goals, making it difficult to incorporate safely and effectively in online settings. We address this problem in the static and dynamic optimization settings by modelling the uncertainty in source and target task functions using normal-inverse-gamma priors, whose corresponding posteriors are, respectively, learned from demonstrations and target data using Bayesian neural networks with shared features. We use this learned belief to derive a quadratic programming problem whose solution yields a probability distribution over the expert models. Finally, we propose Bayesian Experience Reuse (BERS) to sample demonstrations in accordance with this distribution and reuse them directly in new tasks. We demonstrate the effectiveness of this approach for static optimization of smooth functions, and transfer learning in a high-dimensional supply chain problem with cost uncertainty.