FOON Creation and Traversal for Recipe Generation

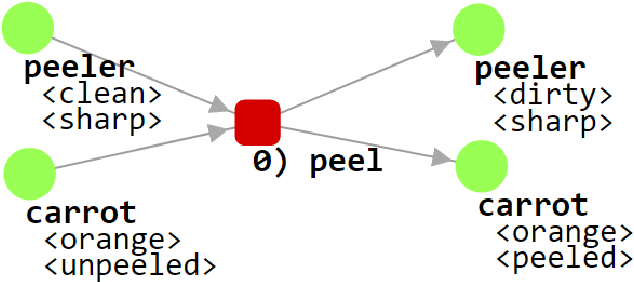
Task competition by robots is still off from being completely dependable and usable. One way a robot may decipher information given to it and accomplish tasks is by utilizing FOON, which stands for functional object-oriented network. The network first needs to be created by having a human creates action nodes as well as input and output nodes in a .txt file. After the network is sizeable, utilization of this network allows for traversal of the network in a variety of ways such as choosing steps via iterative deepening searching by using the first seen valid option. Another mechanism is heuristics, such as choosing steps based on the highest success rate or lowest amount of input ingredients. Via any of these methods, a program can traverse the network given an output product, and derive the series of steps that need to be taken to produce the output.

Quantum-Inspired Tensor Neural Networks for Partial Differential Equations

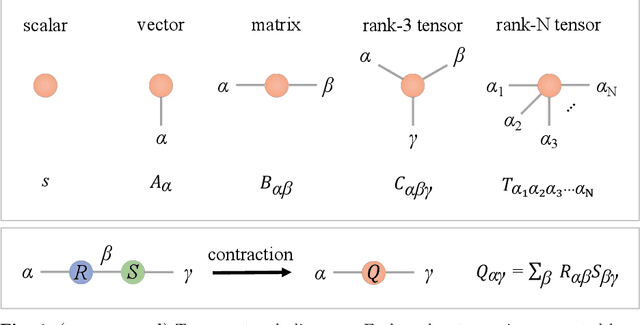
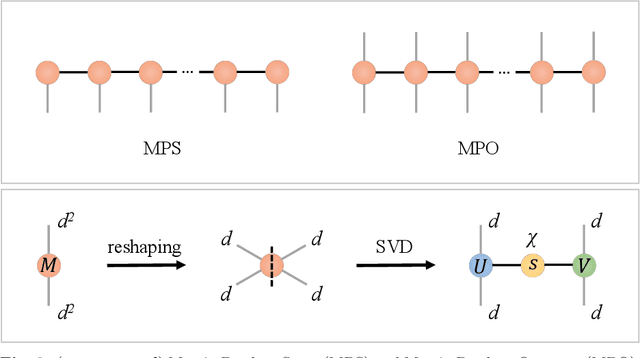
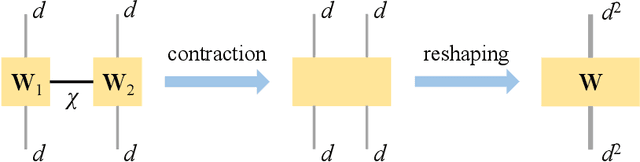
Partial Differential Equations (PDEs) are used to model a variety of dynamical systems in science and engineering. Recent advances in deep learning have enabled us to solve them in a higher dimension by addressing the curse of dimensionality in new ways. However, deep learning methods are constrained by training time and memory. To tackle these shortcomings, we implement Tensor Neural Networks (TNN), a quantum-inspired neural network architecture that leverages Tensor Network ideas to improve upon deep learning approaches. We demonstrate that TNN provide significant parameter savings while attaining the same accuracy as compared to the classical Dense Neural Network (DNN). In addition, we also show how TNN can be trained faster than DNN for the same accuracy. We benchmark TNN by applying them to solve parabolic PDEs, specifically the Black-Scholes-Barenblatt equation, widely used in financial pricing theory, empirically showing the advantages of TNN over DNN. Further examples, such as the Hamilton-Jacobi-Bellman equation, are also discussed.

Estimator Vectors: OOV Word Embeddings based on Subword and Context Clue Estimates

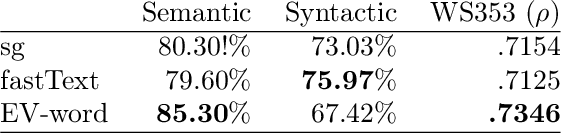
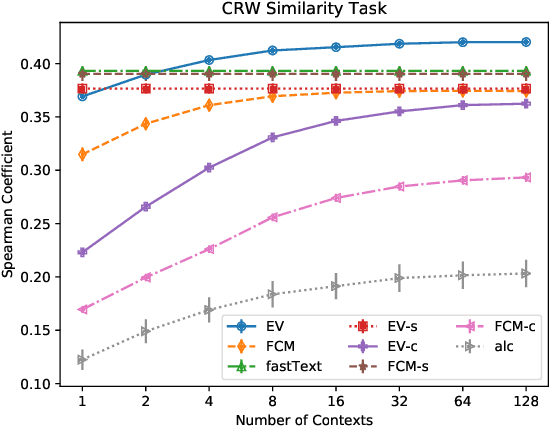
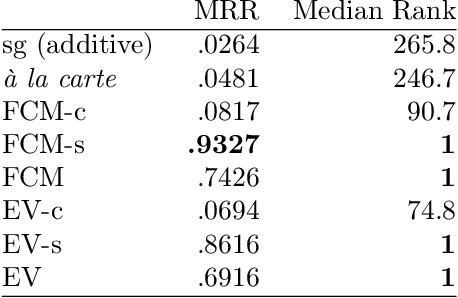
Semantic representations of words have been successfully extracted from unlabeled corpuses using neural network models like word2vec. These representations are generally high quality and are computationally inexpensive to train, making them popular. However, these approaches generally fail to approximate out of vocabulary (OOV) words, a task humans can do quite easily, using word roots and context clues. This paper proposes a neural network model that learns high quality word representations, subword representations, and context clue representations jointly. Learning all three types of representations together enhances the learning of each, leading to enriched word vectors, along with strong estimates for OOV words, via the combination of the corresponding context clue and subword embeddings. Our model, called Estimator Vectors (EV), learns strong word embeddings and is competitive with state of the art methods for OOV estimation.