A plug-and-play framework for curvilinear structure segmentation based on a learned reconnecting regularization

Curvilinear structures are present in various fields in image processing such as blood vessels in medical imaging or roads in remote sensing. Their detection is crucial for many applications. In this article, we propose an unsupervised plug-and-play framework for the segmentation of curvilinear structures that focuses on the preservation of their connectivity. This framework includes an algorithm for generating realistic pairs of connected/disconnected curvilinear structures and a reconnecting regularization operator that can be learned from a synthetic dataset. Once learned, this regularization operator can be plugged into a variational segmentation scheme and used to segment curvilinear structure images without requiring annotations. We demonstrate the interest of our approach on the segmentation of vascular images both in 2D and 3D and compare its results with classic unsupervised and deep learning-based approach. Comparative evaluations against unsupervised classic and deep learning-based methods highlight the superior performance of our approach, showcasing remarkable improvements in preserving the connectivity of curvilinear structures (approximately 90% in 2D and 70% in 3D). We finally showcase the good generalizability behavior of our approach on two different applications : road cracks and porcine corneal cells segmentations.

Restoring Connectivity in Vascular Segmentation using a Learned Post-Processing Model

Accurate segmentation of vascular networks is essential for computer-aided tools designed to address cardiovascular diseases. Despite more than thirty years of research, it remains a challenge to obtain vascular segmentation results that preserve the connectivity of the underlying vascular network. Yet connectivity is one of the key feature of these tools. In this work, we propose a post-processing algorithm aiming to reconnect vascular structures that have been disconnected by a segmentation algorithm. Connectivity being a complex property to model explicity, we propose to learn this geometric feature either through synthetic data or annotations of the application of interest. The resulting post-processing model can be used on the output of any supervised or unsupervised vascular segmentation algorithm. We show that this post-processing effectively restores the connectivity of vascular networks both in 2D and 3D images, leading to improved overall segmentation results.

Deep vessel segmentation based on a new combination of vesselness filters

Vascular segmentation represents a crucial clinical task, yet its automation remains challenging. Because of the recent strides in deep learning, vesselness filters, which can significantly aid the learning process, have been overlooked. This study introduces an innovative filter fusion method crafted to amplify the effectiveness of vessel segmentation models. Our investigation seeks to establish the merits of a filter-based learning approach through a comparative analysis. Specifically, we contrast the performance of a U-Net model trained on CT images with an identical U-Net configuration trained on vesselness hyper-volumes using matching parameters. Our findings, based on two vascular datasets, highlight improved segmentations, especially for small vessels, when the model's learning is exposed to vessel-enhanced inputs.

Discovering Local Binary Pattern Equation for Foreground Object Removal in Videos

Designing a novel Local Binary Pattern (LBP) process usually relies heavily on human experts' knowledge and experience in the area. Even experts are often left with tedious episodes of trial and error until they identify an optimal LBP for a particular dataset. To address this problem, we present a novel symbolic regression able to automatically discover LBP formulas to remove the moving parts of a scene by segmenting it into a background and a foreground. Experimental results conducted on real videos of outdoor urban scenes under various conditions show that the LBPs discovered by the proposed approach significantly outperform the previous state-of-the-art LBP descriptors both qualitatively and quantitatively. Our source code and data will be available online.

Robust reconstructions by multi-scale/irregular tangential covering

In this paper, we propose an original manner to employ a tangential cover algorithm - minDSS - in order to geometrically reconstruct noisy digital contours. To do so, we exploit the representation of graphical objects by maximal primitives we have introduced in previous works. By calculating multi-scale and irregular isothetic representations of the contour, we obtained 1-D (one-dimensional) intervals, and achieved afterwards a decomposition into maximal line segments or circular arcs. By adapting minDSS to this sparse and irregular data of 1-D intervals supporting the maximal primitives, we are now able to reconstruct the input noisy objects into cyclic contours made of lines or arcs with a minimal number of primitives. In this work, we explain our novel complete pipeline, and present its experimental evaluation by considering both synthetic and real image data. We also show that this is a robust approach, with respect to selected references from state-of-the-art, and by considering a multi-scale noise evaluation process.

Automated Mathematical Equation Structure Discovery for Visual Analysis

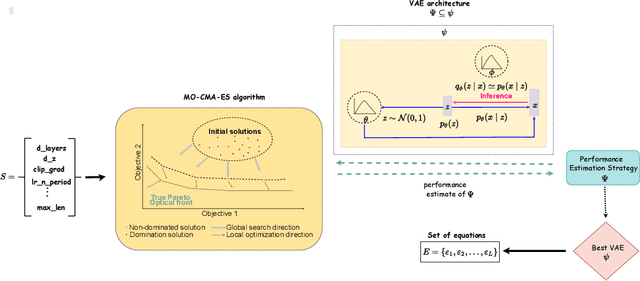
Finding the best mathematical equation to deal with the different challenges found in complex scenarios requires a thorough understanding of the scenario and a trial and error process carried out by experts. In recent years, most state-of-the-art equation discovery methods have been widely applied in modeling and identification systems. However, equation discovery approaches can be very useful in computer vision, particularly in the field of feature extraction. In this paper, we focus on recent AI advances to present a novel framework for automatically discovering equations from scratch with little human intervention to deal with the different challenges encountered in real-world scenarios. In addition, our proposal can reduce human bias by proposing a search space design through generative network instead of hand-designed. As a proof of concept, the equations discovered by our framework are used to distinguish moving objects from the background in video sequences. Experimental results show the potential of the proposed approach and its effectiveness in discovering the best equation in video sequences. The code and data are available at: https://github.com/carolinepacheco/equation-discovery-scene-analysis