Reconstruction of Time-varying Graph Signals via Sobolev Smoothness
Paper and Code
Jul 13, 2022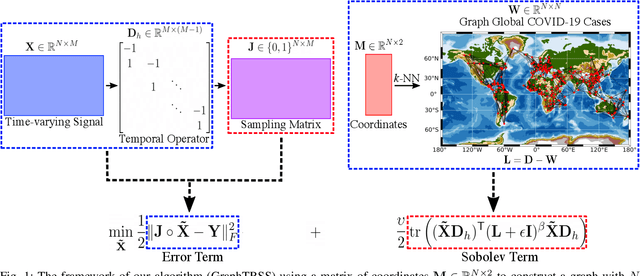
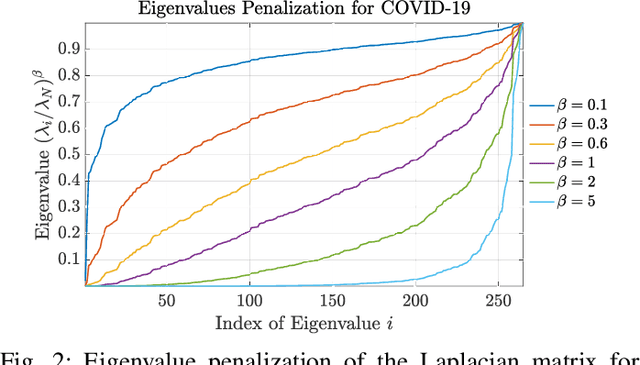
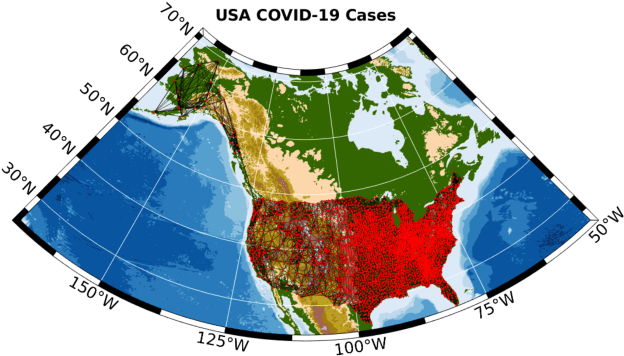
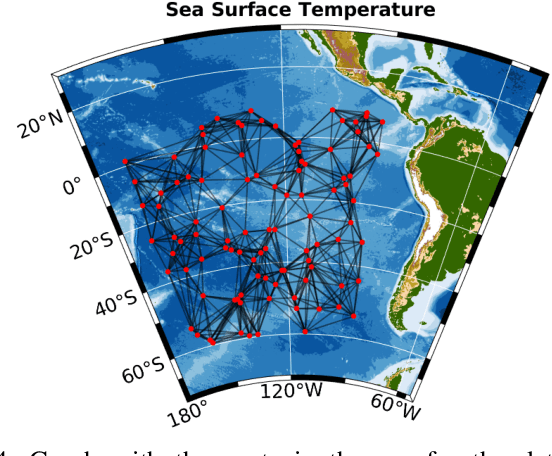
Graph Signal Processing (GSP) is an emerging research field that extends the concepts of digital signal processing to graphs. GSP has numerous applications in different areas such as sensor networks, machine learning, and image processing. The sampling and reconstruction of static graph signals have played a central role in GSP. However, many real-world graph signals are inherently time-varying and the smoothness of the temporal differences of such graph signals may be used as a prior assumption. In the current work, we assume that the temporal differences of graph signals are smooth, and we introduce a novel algorithm based on the extension of a Sobolev smoothness function for the reconstruction of time-varying graph signals from discrete samples. We explore some theoretical aspects of the convergence rate of our Time-varying Graph signal Reconstruction via Sobolev Smoothness (GraphTRSS) algorithm by studying the condition number of the Hessian associated with our optimization problem. Our algorithm has the advantage of converging faster than other methods that are based on Laplacian operators without requiring expensive eigenvalue decomposition or matrix inversions. The proposed GraphTRSS is evaluated on several datasets including two COVID-19 datasets and it has outperformed many existing state-of-the-art methods for time-varying graph signal reconstruction. GraphTRSS has also shown excellent performance on two environmental datasets for the recovery of particulate matter and sea surface temperature signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge