DeFoG: Discrete Flow Matching for Graph Generation
Paper and Code
Oct 05, 2024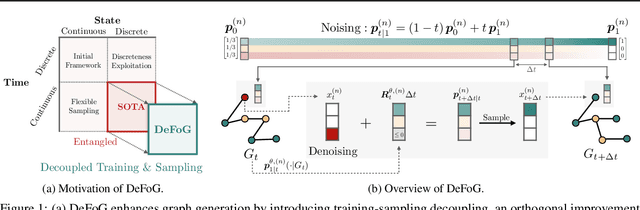


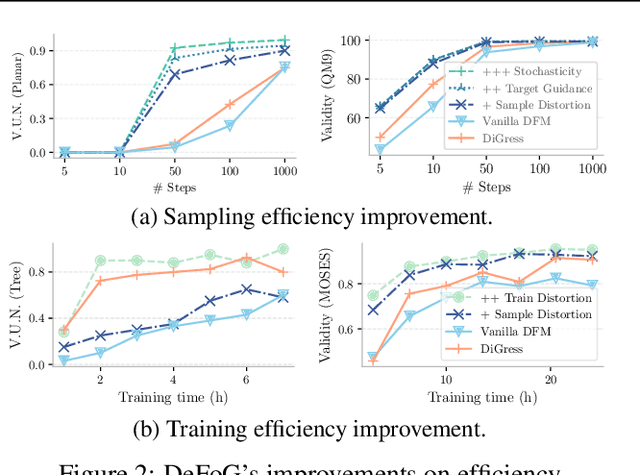
Graph generation is fundamental in diverse scientific applications, due to its ability to reveal the underlying distribution of complex data, and eventually generate new, realistic data points. Despite the success of diffusion models in this domain, those face limitations in sampling efficiency and flexibility, stemming from the tight coupling between the training and sampling stages. To address this, we propose DeFoG, a novel framework using discrete flow matching for graph generation. DeFoG employs a flow-based approach that features an efficient linear interpolation noising process and a flexible denoising process based on a continuous-time Markov chain formulation. We leverage an expressive graph transformer and ensure desirable node permutation properties to respect graph symmetry. Crucially, our framework enables a disentangled design of the training and sampling stages, enabling more effective and efficient optimization of model performance. We navigate this design space by introducing several algorithmic improvements that boost the model performance, consistently surpassing existing diffusion models. We also theoretically demonstrate that, for general discrete data, discrete flow models can faithfully replicate the ground truth distribution - a result that naturally extends to graph data and reinforces DeFoG's foundations. Extensive experiments show that DeFoG achieves state-of-the-art results on synthetic and molecular datasets, improving both training and sampling efficiency over diffusion models, and excels in conditional generation on a digital pathology dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge