Revisiting Automatic Data Curation for Vision Foundation Models in Digital Pathology

Vision foundation models (FMs) are accelerating the development of digital pathology algorithms and transforming biomedical research. These models learn, in a self-supervised manner, to represent histological features in highly heterogeneous tiles extracted from whole-slide images (WSIs) of real-world patient samples. The performance of these FMs is significantly influenced by the size, diversity, and balance of the pre-training data. However, data selection has been primarily guided by expert knowledge at the WSI level, focusing on factors such as disease classification and tissue types, while largely overlooking the granular details available at the tile level. In this paper, we investigate the potential of unsupervised automatic data curation at the tile-level, taking into account 350 million tiles. Specifically, we apply hierarchical clustering trees to pre-extracted tile embeddings, allowing us to sample balanced datasets uniformly across the embedding space of the pretrained FM. We further identify these datasets are subject to a trade-off between size and balance, potentially compromising the quality of representations learned by FMs, and propose tailored batch sampling strategies to mitigate this effect. We demonstrate the effectiveness of our method through improved performance on a diverse range of clinically relevant downstream tasks.

DeFoG: Discrete Flow Matching for Graph Generation

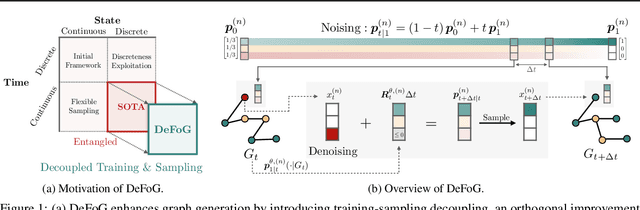
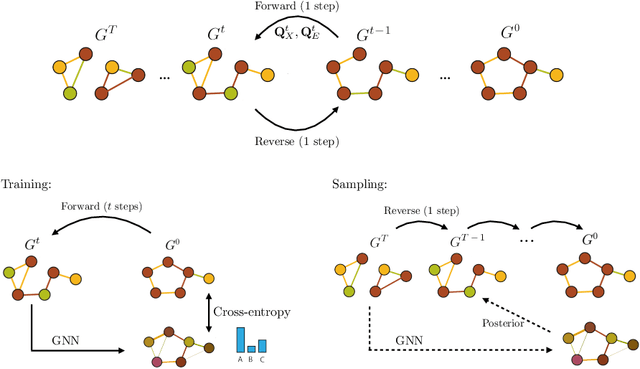
Graph generation is fundamental in diverse scientific applications, due to its ability to reveal the underlying distribution of complex data, and eventually generate new, realistic data points. Despite the success of diffusion models in this domain, those face limitations in sampling efficiency and flexibility, stemming from the tight coupling between the training and sampling stages. To address this, we propose DeFoG, a novel framework using discrete flow matching for graph generation. DeFoG employs a flow-based approach that features an efficient linear interpolation noising process and a flexible denoising process based on a continuous-time Markov chain formulation. We leverage an expressive graph transformer and ensure desirable node permutation properties to respect graph symmetry. Crucially, our framework enables a disentangled design of the training and sampling stages, enabling more effective and efficient optimization of model performance. We navigate this design space by introducing several algorithmic improvements that boost the model performance, consistently surpassing existing diffusion models. We also theoretically demonstrate that, for general discrete data, discrete flow models can faithfully replicate the ground truth distribution - a result that naturally extends to graph data and reinforces DeFoG's foundations. Extensive experiments show that DeFoG achieves state-of-the-art results on synthetic and molecular datasets, improving both training and sampling efficiency over diffusion models, and excels in conditional generation on a digital pathology dataset.

Generative Modelling of Structurally Constrained Graphs

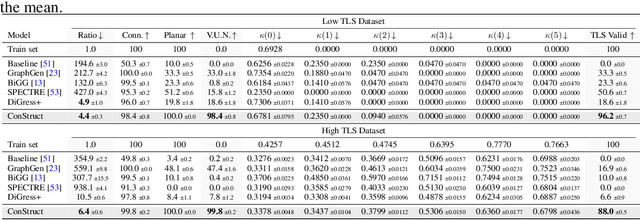
Graph diffusion models have emerged as state-of-the-art techniques in graph generation, yet integrating domain knowledge into these models remains challenging. Domain knowledge is particularly important in real-world scenarios, where invalid generated graphs hinder deployment in practical applications. Unconstrained and conditioned graph generative models fail to guarantee such domain-specific structural properties. We present ConStruct, a novel framework that allows for hard-constraining graph diffusion models to incorporate specific properties, such as planarity or acyclicity. Our approach ensures that the sampled graphs remain within the domain of graphs that verify the specified property throughout the entire trajectory in both the forward and reverse processes. This is achieved by introducing a specific edge-absorbing noise model and a new projector operator. ConStruct demonstrates versatility across several structural and edge-deletion invariant constraints and achieves state-of-the-art performance for both synthetic benchmarks and attributed real-world datasets. For example, by leveraging planarity in digital pathology graph datasets, the proposed method outperforms existing baselines and enhances generated data validity by up to 71.1 percentage points.

Tertiary Lymphoid Structures Generation through Graph-based Diffusion

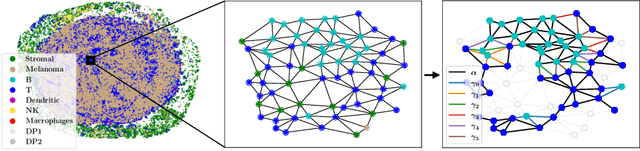
Graph-based representation approaches have been proven to be successful in the analysis of biomedical data, due to their capability of capturing intricate dependencies between biological entities, such as the spatial organization of different cell types in a tumor tissue. However, to further enhance our understanding of the underlying governing biological mechanisms, it is important to accurately capture the actual distributions of such complex data. Graph-based deep generative models are specifically tailored to accomplish that. In this work, we leverage state-of-the-art graph-based diffusion models to generate biologically meaningful cell-graphs. In particular, we show that the adopted graph diffusion model is able to accurately learn the distribution of cells in terms of their tertiary lymphoid structures (TLS) content, a well-established biomarker for evaluating the cancer progression in oncology research. Additionally, we further illustrate the utility of the learned generative models for data augmentation in a TLS classification task. To the best of our knowledge, this is the first work that leverages the power of graph diffusion models in generating meaningful biological cell structures.

COCO Denoiser: Using Co-Coercivity for Variance Reduction in Stochastic Convex Optimization

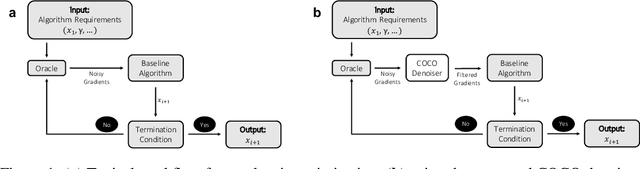
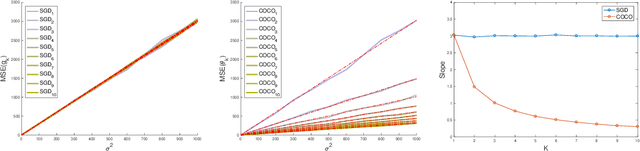
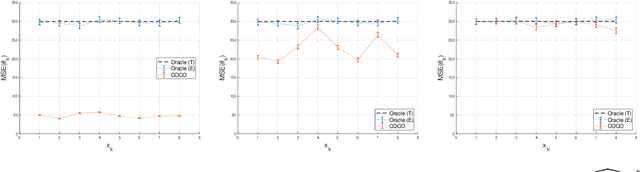
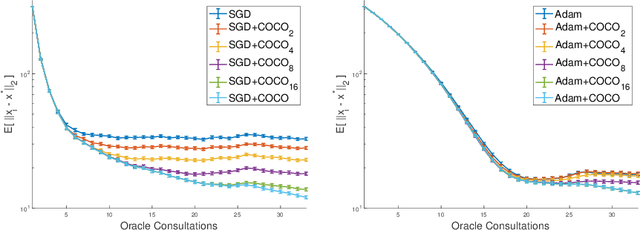
First-order methods for stochastic optimization have undeniable relevance, in part due to their pivotal role in machine learning. Variance reduction for these algorithms has become an important research topic. In contrast to common approaches, which rarely leverage global models of the objective function, we exploit convexity and L-smoothness to improve the noisy estimates outputted by the stochastic gradient oracle. Our method, named COCO denoiser, is the joint maximum likelihood estimator of multiple function gradients from their noisy observations, subject to co-coercivity constraints between them. The resulting estimate is the solution of a convex Quadratically Constrained Quadratic Problem. Although this problem is expensive to solve by interior point methods, we exploit its structure to apply an accelerated first-order algorithm, the Fast Dual Proximal Gradient method. Besides analytically characterizing the proposed estimator, we show empirically that increasing the number and proximity of the queried points leads to better gradient estimates. We also apply COCO in stochastic settings by plugging it in existing algorithms, such as SGD, Adam or STRSAGA, outperforming their vanilla versions, even in scenarios where our modelling assumptions are mismatched.