COCO Denoiser: Using Co-Coercivity for Variance Reduction in Stochastic Convex Optimization
Paper and Code
Sep 07, 2021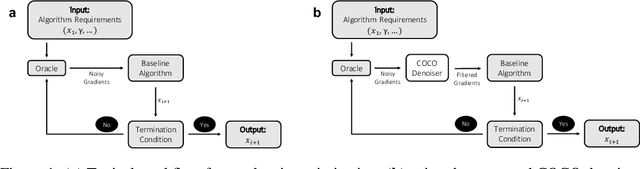
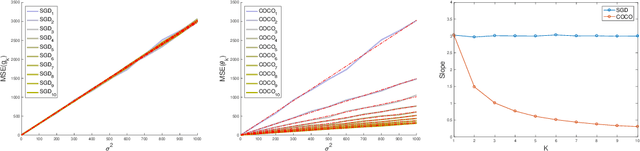
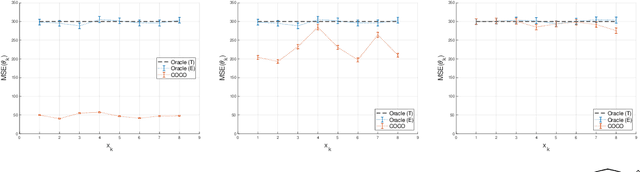
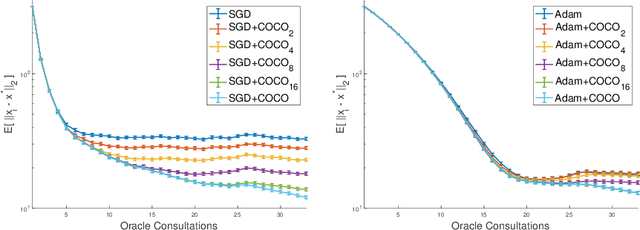
First-order methods for stochastic optimization have undeniable relevance, in part due to their pivotal role in machine learning. Variance reduction for these algorithms has become an important research topic. In contrast to common approaches, which rarely leverage global models of the objective function, we exploit convexity and L-smoothness to improve the noisy estimates outputted by the stochastic gradient oracle. Our method, named COCO denoiser, is the joint maximum likelihood estimator of multiple function gradients from their noisy observations, subject to co-coercivity constraints between them. The resulting estimate is the solution of a convex Quadratically Constrained Quadratic Problem. Although this problem is expensive to solve by interior point methods, we exploit its structure to apply an accelerated first-order algorithm, the Fast Dual Proximal Gradient method. Besides analytically characterizing the proposed estimator, we show empirically that increasing the number and proximity of the queried points leads to better gradient estimates. We also apply COCO in stochastic settings by plugging it in existing algorithms, such as SGD, Adam or STRSAGA, outperforming their vanilla versions, even in scenarios where our modelling assumptions are mismatched.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge